Тема 21. Малые колебания системы

Консервативная механическая система, состоящая из n материальных точек и имеющая одну степень свободы, находится в некотором положении в устойчивом равновесии. Исследуем, какое движение будет совершать эта система, если ее вывести из равновесия малым возмущением. Условимся опять определять положение системы обобщенной координатой q, выбранной так, что при равновесии q = 0. Так как равновесие устойчиво, а возмущения малы, то координата q и обобщенная скорость q́ будут во время движения оставаться величинами малыми. Для составления дифференциального уравнения движения системы воспользуемся уравнением Лагранжа, которое, если выразить обобщенную силу Q через потенциальную энергию системы П, примет вид

. (3.1.177)

Это уравнение будет нелинейным, но его можно линеаризировать и тем самым существенно упростить, сохранив в уравнении малые величины q и только в первой степени. Для этого значения Т(q, ) и П(q) достаточно определить тоже приближенно. При этом, так как в уравнение входят первые производные от П и Т по q и , то, чтобы сохранить в нем q и в первой степени, надо Т и П определить с точностью до малых величин второго порядка малости, т.е. с точностью q² и .

Найдем приближенное выражение Т (q, ). Для любой точки системы при стационарных связях

r_k = r_k(q);

V_k =

Тогда вынося общий множитель за скобки, получим

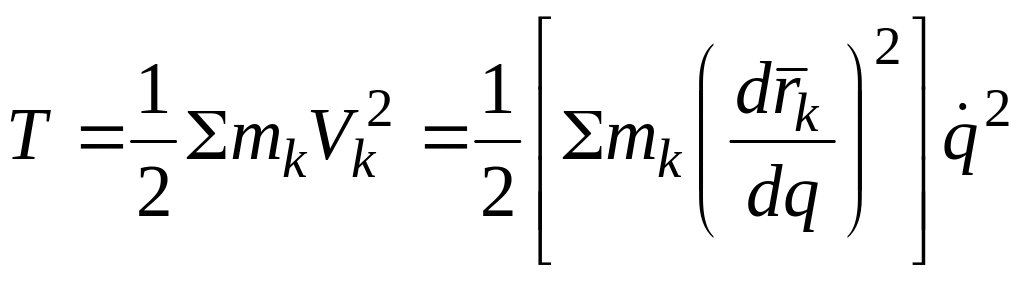
или

Т =

При разложении в ряд Тейлора F(q) получим

F(q) = F(0) + (0)q + ... .

Так как Т надо определить с точностью до q², то в этом разложении следует сохранить только первое постоянное слагаемое F(0). Тогда для Т получим выражение

Т = , (3.1.178)

где а = F(0).

Поскольку величина Т существенно положительная, то постоянный коэффициент а > 0; его называют инерционным коэффициентом. Размерность а зависит от размерности ; в частности, а может иметь размерность массы или момента инерции.

При разложении в ряд Тейлора П(q) получим

П(q) = П(0) + , (3.1.179)

где с = .

При этом с > 0. В частном случае, если q – удлинение пружины, равенство (3.1.179) выражает потенциальную энергию поля сил упругости; поэтому коэффициент с называют обобщенным коэффициентом жесткости.

Из равенств (1.178) и (1.179) находим

Подставляя эти величины в уравнение (3.1.177), получим дифференциальное уравнение малых свободных колебаний системы с одной степенью свободы:

(3.1.180)

где k² = c/a.

Это уравнение соответствует уравнению свободных прямолинейных колебаний материальной точки и его общее решение имеет вид

q = A sin(kt +),

где А и α – постоянные интегрирования, определяемые по начальным условиям.

Частота и период этих колебаний определяются равенствами

k = ; τ = 2π/k = 2π . (3.1.181)

Установим, как при этом движутся точки системы. Разлагая радиус-вектор одной их точек системы в ряд Тейлора и заменяя q его значением найдем, что точки системы тоже совершают малые колебания с частотой k и амплитудами . Из найденных результатов вытекают следующие свойства малых колебаний системы:

1. Свободные колебания системы являются колебаниями гармоническими; частота и период этих колебаний не зависят от начальных условий и определяются равенствами (3.1.181).

2. Так как постоянные А и α зависят от начальных условий, то амплитуды колебаний точек системы, равные , и начальная фаза тоже зависят от начальных условий.

3. Отношения амплитуд колебаний разных точек системы от начальных условий не зависят, так как определяются только значениями , т.е. конфигурацией системы;

4. Все точки системы в каждый момент времени находятся в одной и той же фазе (kt + α) и, следовательно, одновременно проходят через положения равновесия и одновременно достигают максимальных отклонений от этого положения.

При решении задач наибольший интерес представляет определение частоты k и периода τ собственных колебаний системы, что существенно, например, для установления условий наличия или отсутствия резонанса.