Тема 3. Кинематический анализ механизмов

Кинематический анализ. Кинематическое исследование механизма состоит в изучении движения звеньев без учета сил, действующих на эти звенья, при заданном движении ведущего звена.

Кинематический анализ выполняется по кинематической схеме механизма. Он состоит в определении кинематических характеристик:

• перемещений звеньев и траекторий, описываемых характерными точками звеньев;

• линейных скоростей и ускорений точек звеньев механизма;

• угловых скоростей и угловых ускорений звеньев механизма.

Кинематический анализ позволяет установить соответствие кинематических параметров (перемещений, скоростей и ускорений) заданному закону движения механизма, а также получить исходные данные для выполнения динамического анализа. По полученным кинематическим характеристикам определяют инерционные нагрузки звеньев, кинетическую энергию механизма, закон движения ведущего и ведомых звеньев в функции времени.

Кинематическое исследование механизмов проводят графическими и аналитическими методами. Графическое определение кинематических параметров основано на геометрических построениях, погрешность результатов которых составляет 0,3–0,5 % по сравнению с аналитическими расчетами.

Графический метод нагляден и универсален, так как позволяет определять положения, скорости и ускорения звеньев механизма любой структуры. Метод построения планов скоростей и ускорений применяется при инженерных расчетах как при анализе, так и при синтезе механизмов. Графический метод построения кинематических диаграмм позволяет использовать при анализе заданные в виде графиков законы изменения кинематических параметров в функции обобщенных координат  и t. Точность графических методов достаточна для выполнения технических расчетов. Графические методы не могут быть использованы, если требуется проводить расчеты с высокой точностью. Применение ЭВМ при аналитическом исследовании упрощает выполнение сложных и трудоемких вычислений.

При кинематическом исследовании различают абсолютное и относительное движения звеньев и кинематических пар механизма и соответствующие им кинематические характеристики.

Абсолютное движение – движение точки или тела относительно неподвижной системы координат, связанной с не подвижными стойкой или корпусом.

Относительное движение – движение точки или звена относительно подвижной системы координат, которая связана с каким-либо движущимся звеном. Движение подвижной системы координат относительно неподвижной системы координат называется переносным движением.

Перемещение (как скалярная величина) – мера пути, пройденного точкой или звеном за некоторое время: линейное перемещение (S) измеряется в метрах, угловое () – в градусах или радианах.

Угол в 1 рад соответствует центральному углу окружности, длина дуги которой равна ее радиусу. В окружности 2 таких отрезков, поэтому 1 рад = 360/(2) = 57,3°.

Скорость – основная кинематическая характеристика (векторная величина) – мера быстроты движения, характеризующая перемещение точки в рассматриваемый момент времени (в рассматриваемом положении) в данной системе отсчета. Линейная скорость (V) измеряется в м/с, угловая () – в с^–1.

Ускорение (векторная величина) – мера быстроты изменения скорости в данный момент в данной системе отсчета. Размерность линейного ускорения а (м/с²), углового  (с^–2).

Из теоретической механики известна теорема сложения скоростей:

Вектор абсолютной скорости точки В звена равен геометрической сумме вектора скорости произвольно выбранной точки А звена и вектора скорости во вращательном движении относительно этой точки.

Это уравнение для точки В звена (рис. 3.3.9, а) имеет вид

.

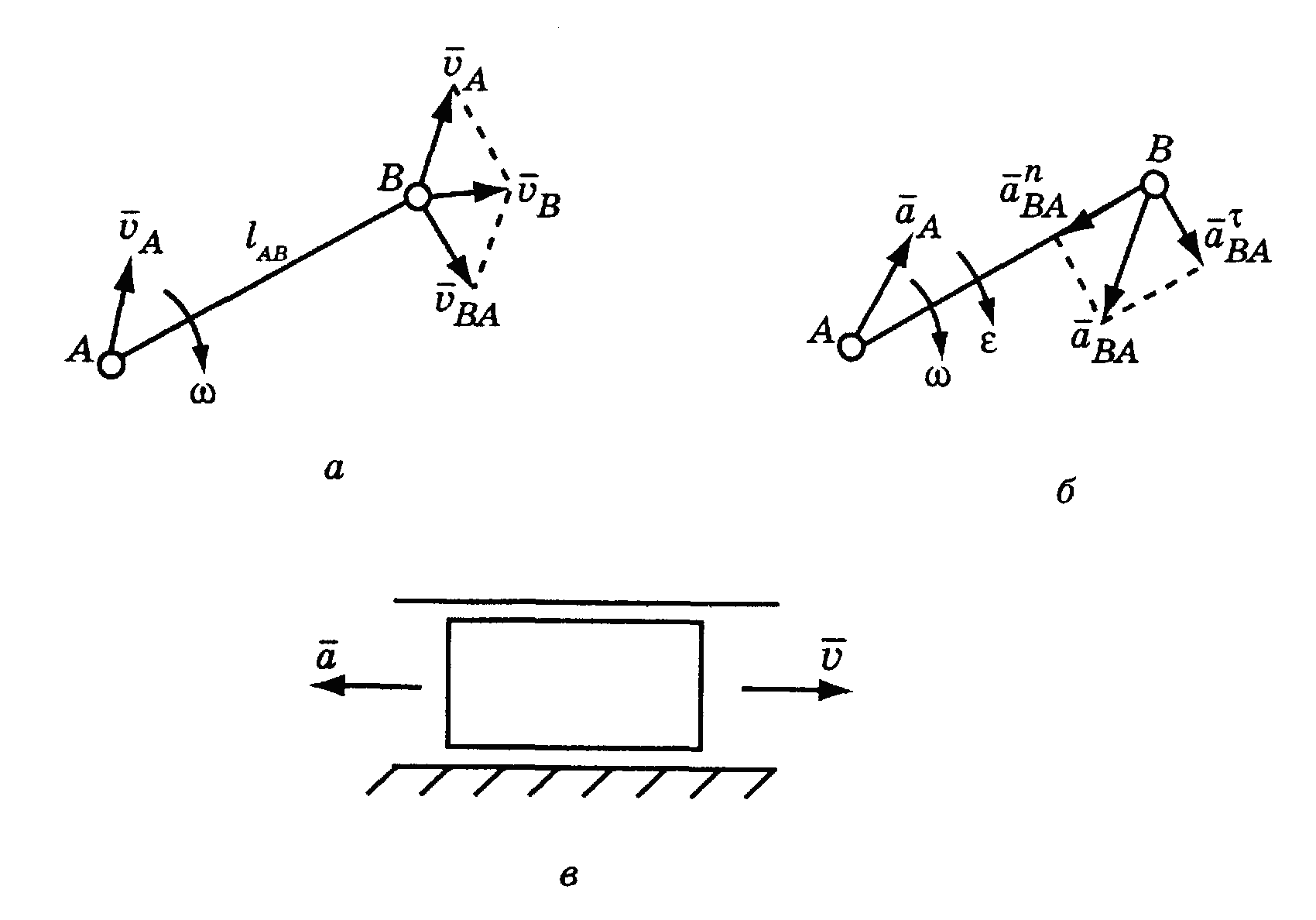
Рис. 3.3.9

Вектор скорости известен по величине и направлению.

Вектор линейной скорости точки звена во вращательном движении направлен в сторону движения звена (по угловой скорости со звена) по касательной к траектории, т.е. перпендикулярно звену ВА ( BА).

Вектор абсолютного ускорения точки В звена равен геометрической сумме вектора ускорения произвольно выбранной точки А и вектора ускорения во вращательном движении относительно этой точки (рис. 3.3.9, б).

,

где – соответственно относительное нормальное (центростремительное) и касательное (тангенциальное) ускорения во вращательном движении.

Нормальное ускорение направлено по радиусу вращения точки к центру кривизны траектории (вдоль звена от точки В к точке А), а касательное ускорение направлено перпендикулярно звену АВ в сторону углового ускорения е звена (см. рис. 3.3.9, б).

Направление угловой скорости  и углового ускорения  совпадают при равноускоренном движении звена и противоположны друг другу при равнозамедленном движении.

При поступательном движении звена векторы абсолютных скоростей и абсолютных ускорений всех точек звена равны и направлены по касательной к траектории движения. Направление векторов скоростей совпадает с направлением движения, а для ускорений при ускоренном движении эти векторы направлены в сторону движения, при замедленном – в обратную сторону (рис. 3.3.9, в).

Планы положений механизма. Планом положений механизма называется графическое изображение кинематической схемы в выбранном масштабе, соответствующее заданному положению начального звена.

Планы строятся в заданном масштабе. При этом различают понятия «масштаб» и «масштабный коэффициент». Масштабом физической величины называют длину отрезка в миллиметрах, изображающую единицу измерения этой величины. Масштабным коэффициентом физической величины называют отношение численного значения физической величины к длине отрезка в миллиметрах, изображающего эту величину. Масштаб и масштабный коэффициент являются взаимно обратными величинами. Масштабные коэффициенты обозначают буквой  с индексом, указывающим, к какой величине они относятся. Например, масштабный коэффициент длин (_l) для плана механизма есть отношение какой-либо длины (l_AB) в метрах к отрезку (АВ), изображающему эту длину на чертеже в миллиметрах:

.

Рассмотрим построение планов механизма на примерах.

1. Шарнирный четырехзвенник (рис. 3.3.10). Кривошип ОА вращается с постоянной скоростью , поэтому положение точки А известно для любого момента времени (любого угла поворота звена ОА).

Рис. 3.3.10

Делим окружность радиуса ОА на несколько равных частей, например, на 6. Обозначим положения конца кривошипа точками А₁, А₂, …, А₆.

Точка В (конец коромысла) движется по дуге окружности радиуса СВ. Проведем эту дугу из центра – точки С.

Радиусом, равным длине шатуна АВ, делаем из точек А₁, A₂, ... A₆ засечки на дуге окружности.

Соединяем одноименные положения точек А₁ и В₁, А₂ и В₂, а также В₁ и С₁, В₂ и С₂. Получаем положения шатуна и коромысла за цикл движения, т. е. за один оборот кривошипа. Вращение коромысла против часовой стрелки соответствует положениям рабочего хода, по часовой стрелке – положениям холостого хода.

2. Кривошипно-ползунный механизм (рис. 3.3.11). Задаемся крайним положением кривошипа (кривошип и шатун располагаются на одной линии).

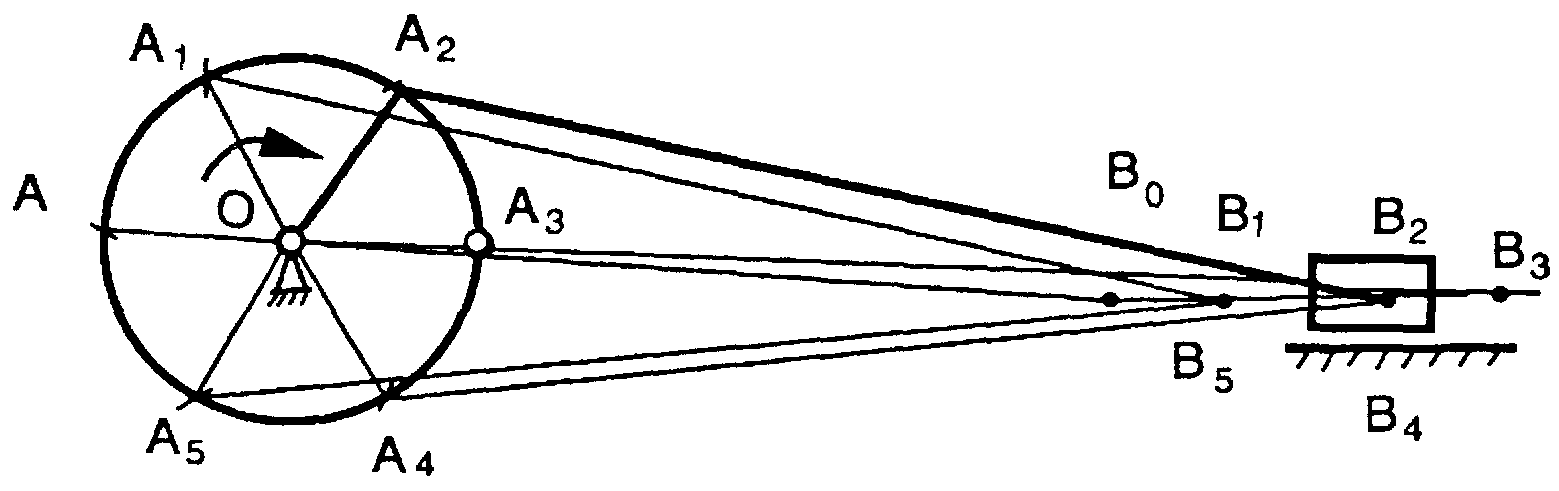
Рис. 3.3.11

Делим окружность радиуса ОА на равные части. Из точек деления (А₁, А₂, ...) делаем засечки на оси движения ползуна (В₁, В₂, ...) радиусом, равным длине шатуна. Найденные положения точки В определяют положение поршня (ползуна) на рабочем ходу – В₁, В₂, В₃; на холостом ходу – В₄, В₅. Соединяем одноименные точки (А₁ и B₁, A₂ и В₂ и т.д.).

Планы скоростей плоских механизмов. Планом скоростей называют чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек механизма в данном положении.

Для построения плана скоростей необходимы исходные данные:

• план механизма с указанием размеров;

• угловая скорость начального звена.

Из теоретической механики известно, что любое движение плоского тела может рассматриваться как сумма двух движений: вращение относительно некоторой точки (полюса) и поступательное (переносное) движение полюса. Используя этот принцип, рассмотрим решение задач о скоростях точек звеньев, образующих пары 5-го класса.

Пример. Определение скоростей точек звена, входящего во вращательную пару с другим звеном (рис. 3.3.12).

П усть заданы: – вектор скорости точки А (см. рис. 3.3.12, а); _АВ – угловая скорость звена АВ.

Требуется определить: скорости точек В и С (V_B, V_С ).

В соответствии с теоремой сложения скоростей, абсолютная скорость (V_B) точки равна геометрической сумме переносной (V_A) и относительной (V_ВА) скоростей этой точки:

, (3.3.1)

где V_BA = _AB l_AB – относительная скорость точки В во вращательном движении вокруг точки А; вектор V_BA направлен перпендикулярно звену АВ (т. е. радиусу вращения).

2. Аналогично

, (3.3.2)

где V_CA = _AB l_AC; вектор этой скорости направлен перпендикулярно звену АС (V_CA  AC).

3. Построим векторные уравнения (3.3.1) и (3.3.2).

Выбираем произвольную точку р – полюс плана скоростей и откладываем в направлении вектора V_A отрезок произвольной длины ра (см. рис. 3.3.12, б). При этом определяем значение масштабного коэффициента плана скоростей:

_у = V_А/ра. (3.3.3)

Строим вектор . Из точки а проводим прямую, перпендикулярную аb, и откладываем отрезок аb в масштабе, учитывая при этом направление угловой скорости _АВ:

. (3.3.4)

Суммарный вектор – абсолютная скорость точки В – определится отрезком рb:

. (3.3.5)

Аналогично находим скорость точки с: из точки а в направлении, перпендикулярном ас, откладываем относительную скорость с учетом масштабного коэффициента:

ac = _ABl_AC /_V. (3.3.6)

Соединяем полюс с полученной на плане скоростей точкой с. Измерив на плане величину отрезка рс, находим значение абсолютной скорости точки с:

(3.3.7)

Скорость точки С можно определить, приняв движение точки в за переносное:

(3.3.8)

На плане скоростей вектор pb изображает скорость точки в; относительная скорость V_cb – это вектор bc , направленный перпендикулярно стороне звена ВС (см. рис. 3.3.12, а). Соединив точки b и с, получим на плане скоростей графическое изображение уравнения (3.3.8).

Сравнивая треугольники ABC и аbс на рис. 3.3.12, можно заметить, что эти фигуры подобны и сходственны, т. к. стороны их взаимно перпендикулярны и отрезки ab, ас, bс пропорциональны длинам сторон звена АВ, АС, ВС.

Выводы:

1. На плане скоростей лучи, выходящие из полюса, изображают абсолютные скорости точек звена, а отрезки, соединяющие концы лучей, – относительные скорости соответствующих точек.

2. Векторы относительных скоростей направлены на плане скоростей к первой букве индекса. Например, V_CB – скорость точки С относительно В. На плане скоростей читается наоборот: отрезок bc , а вектор направлен к точке с.

3. Векторы относительных скоростей точек жесткого звена образуют на плане скоростей фигуру, подобную этому звену, повернутую на 90° в направлении угловой скорости звена.

Последний вывод называется принципом подобия в плане скоростей и позволяет определить скорость любой точки звена графически, если известны скорости хотя бы двух точек этого звена.

Планы ускорений плоских механизмов. Чертеж, на котором изображены в виде отрезков векторы, равные по модулю и направлению ускорениям различных точек звеньев механизма в данном положении, называется планом ускорений.

Рассмотрим решение двух задач об определении ускорений точек звеньев, образующих кинематические пары 5-го класса, аналогично решению задач о скоростях.

Пример. Определите ускорение точек звена, входящего во вращательную пару (рис. 3.3.13).

П ри построении плана ускорений считается, что все скорости известны, т. е. план скоростей механизма для данного положения уже построен.

– ускорение точки А; – угловое ускорение звена ABC.

Решение.

1. Абсолютное ускорение точки В складывается из переносного ускорения ( ) и относительного ускорения ( ) во вращательном движении точки В вокруг А (см. рис. 3.3.13, а):

. (3.3.9)

2. Поскольку относительное движение вращательное, выражение (3.3.9) можно записать в виде

, (3.3.10)

где – нормальное ускорение в относительном движении, направленное по радиусу вращения (АВ) к центру вращения (точке А);

– касательное ускорение в относительном движении, направленное перпендикулярно радиусу вращения.

3. Построим уравнение (3.3.10) в виде суммы векторов (см. рис. 3.3.13, б). Выбираем точку  – плюс плана ускорений. Откладываем из полюса вектор отрезка произвольной длины а, направленного параллельно вектору . Определяем масштабный коэффициент:

_а = а_А/а. (3.3.11)

Из точки а откладываем в направлении к центру вращения с учетом масштаба вектор нормального ускорения (anBA). Величина отрезка an определяется соотношением

. (3.3.12)

От полученной точки n в направлении, перпендикулярном АВ, откладываем отрезок nb, изображающий в масштабе касательную, составляющую относительного ускорения:

. (3.3.13)

Направление вектора nb определяется с учетом направления углового ускорения (в данном примере – вниз).

Соединяя точку п с точкой b, получаем результирующий вектор, который изображает абсолютное ускорение точки В (см. уравнение (3.3.10)):

. (3.3.14)

Аналогично строятся векторные уравнения для точки С (см. рис. 3.3.13):

; (3.3.15)

. (3.3.16)

4. Определим значения полных относительных ускорений:

. (3.3.17)

5. С учетом известных из теоретической механики формул (см. значения величин, входящих в уравнение (3.3.10))

. (3.3.18)

Аналогично

; (3.3.19)

. (3.3.20)

6. Определим тангенс угла, определяющего направление полного относительного ускорения (см. рис. 3.3.12, а):

. (3.3.21)

Из формулы (3.3.21) следует, что tg не зависит от того, какая точка звена рассматривается, и одинаков для всех относительных ускорений.

Из выражений (3.3.18) – (3.3.21) следует, что относительные ускорения точек звена ABC пропорциональны длинам сторон и повернуты на один и тот же угол. Следовательно, abc в плане ускорений и АВС (жесткое звено) подобны и сходственны.

Этим определяется принцип подобия в плане ускорений.

Векторы относительных ускорений точек жесткого звена образуют на плане ускорений фигуру, подобную этому звену и повернутую относительно его на угол (180° – ) в направлении углового ускорения.

Зная относительные ускорения хотя бы двух точек звена, можно определить ускорение любой точки этого звена, пользуясь принципом подобия.