Контрольные вопросы

1. Какие основные понятия используются в статике?

2. Охарактеризуйте понятие сосредоточенной и распределенной сил.

3. Какие системы сил называются эквивалентными, какие – уравновешенными?

4. Какую силу называют равнодействующей?

5. Сформулируйте аксиомы статики.

6. Основные типы связей. Направление их реакций.

7. Какая система сил называется сходящейся? Как найти равнодействующую системы сходящихся сил.

8. Назовите аналитические условия равновесия системы сходящихся сил, расположенных на плоскости и в пространстве.

9. Теорема о равновесии трех непараллельных сил.

10. Чему равен момент силы относительно точки? Когда он равен нулю?

11. В каких случаях момент силы относительно оси равен нулю?

12. Что такое пара сил? Чему равен момент пары?

13. Как суммируются пары сил? Чем может быть заменена система пар сил, действующих на твердое тело?

14. Что такое пара сил трения качения? Почему она возникает? От чего зависит ее момент?

15. Теорема о параллельном переносе силы.

16. Приведение произвольной плоской системы сил к данному центру. Главный вектор и главный момент.

17. Аналитические условия равновесия различных систем сил.

18. Теорема о моменте равнодействующей произвольной пространственной системы сил относительно точки и оси (теорема Вариньона).

19. Дайте определение центра параллельных сил и центра тяжести твердого тела.

20. Запишите формулы, по которым вычисляются координаты центров тяжести простейших фигур.

21. Перечислите основные способы, используемые при определении положения центров тяжести твердых тел.

22. Как определяется положение центров тяжести симметричных тел?

Кинематика

Тема 7. Основные понятия кинематики.

Способы задания движения

Кинематика – раздел теоретической механики, в котором изучается механическое движение без учета масс и приложения сил. Всякое движение тел происходит в пространстве и во времени, по отношению к другим телам, с которыми жестко связывают систему координат, называемую системой отсчета. Абсолютно неподвижных тел в окружающем нас мире нет, поэтому движение и покой любого тела являются относительными. При изучении движения ВС по аэродрому или при полетах на небольшие расстояния Землю считают неподвижной и связывают с ней систему отсчета. При скоростных полетах на большие расстояния систему отсчета по-прежнему связывают с Землей, но не считают ее неподвижной, а учитывают суточное, а в некоторых случаях и годовое движение. При расчетах движения космических кораблей систему отсчета связывают с Солнцем и так называемыми «неподвижными» звездами.

Для измерения расстояний в пространстве используют единицу длины метр.

Время в механике считают скалярной, непрерывно изменяющейся величиной, одинаковой для всех систем отсчета. За единицу времени принята секунда.

Для характеристики рассматриваемого движения в механике пользуются понятиями «траектория точки», «скорость точки» и «ускорение точки».

Траекторией называют множество последовательных положений движущейся точки в рассматриваемой системе отсчета.

Скоростью точки называют пространственно-временную меру, характеризующую быстроту и направление движения точки.

Ускорением точки называют пространственно-временную меру, характеризующую изменение абсолютной величины и направления скорости.

Способы задания движения точки. Определение скорости и ускорения точки. Для задания движения точки в пространстве пользуются каким-либо одним из трех основных способов: векторным, координатным, естественным.

Векторный способ. Положение точки в пространстве однозначно определяется заданием радиуса-вектора , проведенного из некоторого неподвижного центра О в данную точку М. Для определения движения точки должна быть задана вектор-функция аргумента t (рис. 3.1.47):

= f(t). (3.1.40)

Траекторией точки является годограф радиус-вектора.

Вектор скорости точки в данный момент времени t равен первой производной от радиус-вектора точки по времени и направлен по касательной к траектории точки в сторону движения (рис. 3.1.48).

. (3.1.41)

Скорость – это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета. Скорость измеряется в м/с.

Ускорением точки называется вектор, характеризующий быстроту изменения вектора скорости (рис. 3.1.49)

. (3.1.42)

У скорение точки равно первой производной от вектора скорости или второй производной от радиуса вектора точки по времени. Вектор ускорения точки всегда направлен в сторону вогнутости траектории и лежит в так называемой соприкасающейся плоскости.

Координатный способ. Рассмотрим движение точки в прямоугольной системе декартовых координат (рис. 3.1.50). Положение точки М в системе отсчета OXYZ определяется тремя декартовыми координатами точки x, y, z:

x = f₁(t); y = f₂(t); z = f₃(t). (3.1.43)

Уравнение (3.1.43) задает движение точки в декартовых координатах. Обозначим орты осей координат за . Проведем из начала координат в движущуюся точку М радиус-вектор , где , тогда

, (3.1.44)

где V_x = , V_y = , V_z = – проекции вектора скорости точки на неподвижные оси декартовых координат. Модуль и направление вектора скорости

V = = , (3.1.45)

(3.1.46)

Ускорение точки определяем, зная, что

= = , (3.1.47)

где = , = , = – проекции ускорения на координатные оси.

Модуль и направляющие косинусы вектора ускорения:

, (3.1.48)

cos = ; cos = ; cos = . (3.1.49)

Естественный способ. Движение точки определено, если заданы (рис. 3.1.51):

• траектория, положение которой относительно выбранной системы отсчета известно;

• начало и направление отсчета дуговой координаты;

• уравнение движения

S = f (t), (3.1.50)

связывающее расстояние движущейся точки от начала отсчета со временем. В общем случае расстояние (S) не равно пройденному точкой М пути, так как точка может начать движение не из начала отсчета, а из другого положения (М₁). Численное значение скорости определяется по формуле

, (3.1.51)

т.е. равно первой производной по времени от расстояния.

Знак скорости показывает направление движения точки в данный момент. При знаке «плюс» точка движется в сторону положительного отсчета расстояний и наоборот.

При естественном способе задания движения ускорение точки определяют его составляющими, направленными по так называемым естественным осям. Траектория точки, как и любая кривая, имеет три естественные оси (рис. 3.1.52):

• касательную (орт оси – ) – ось, направленная в сторону положительного отсчета;

• главную нормаль (орт оси – ) – линию пересечения соприкасающейся и нормальной плоскостей, направленную в сторону вогнутости кривой;

• бинормаль (орт оси – ) – ось, перпендикулярную касательной и главной нормали.

Кривизной кривой (K) в данной точке называют предел отношения угла смежности (рис. 3.1.53) к длине дуги ΔS, ему соответствующей, при ΔS→0: K = lim Δφ/ ΔS.

В еличина, обратная кривизне K, называется радиусом кривизны: .

Ускорение точки лежит в соприкасающейся плоскости и равно производной от вектора скорости по времени (рис. 3.1.54).

П редставим вектор скорости как произведение ее численного значения V на орт касательный :

, (3.1.52)

. (3.1.53)

Первое слагаемое есть касательное ускорение точки, характеризующее изменение вектора скорости этой точки только по модулю:

. (3.1.54)

Рассмотрим второе слагаемое. Величину | | найдем, взяв предел отношения │Δτ│ к ∆t при ∆t → 0. Получим , где – единичный вектор, направленный по главной нормали, ρ – радиус кривизны траектории.

Тогда – составляющая ускорения точки вдоль главной нормали к траектории называется нормальным ускорением точки и характеризует изменение направления вектора скорости:

. (3.1.55)

Нормальное ускорение всегда направлено к центру кривизны траектории

Полное ускорение определяется по формуле

. (3.1.56)

Модуль ускорения и его направление определяют по формулам:

; (3.1.57)

или , , (3.1.58)

tg α = . (3.1.59)

Движение точки будет ускоренным (рис. 3.1.55, а), если направление векторов скорости и касательного ускорения совпадает, и замедленным (рис. 3.1.55, б), если наоборот.

Прямолинейное равномерное движение точки – единственный вид движения, при котором ускорение точки равно нулю:

V = const; ρ = ∞; .

Рис. 3.1.55

Прямолинейное неравномерное движение точки характеризуется изменением скорости по модулю:

V≠ const; ; ρ = ∞ , = 0; .

Криволинейное и равномерное движение точки характеризуется изменением направления скорости:

ρ ≠ ∞; ≠ 0, V = const; , .

Криволинейное неравномерное движение точки:

ρ ≠ ∞; V ≠ const; ; ; ,

dV/dt = a_ = const; , V = V₀  a_t. (3.1.60)

Скорость и уравнение равнопеременного движения точки:

V = = V₀ + a_t ; ;

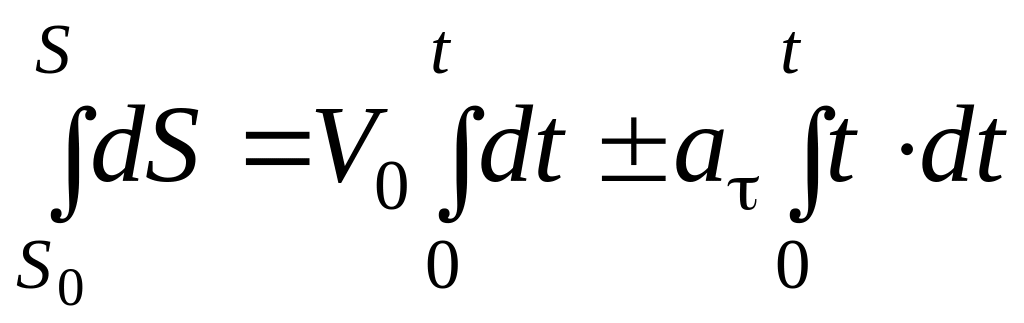S = S₀ + V₀t  . (3.1.61)

Уравнение равнопеременного движения точки при S₀ = 0, V₀ = 0:

.

Пример 1. Посадочная скорость самолета (V_пос) равна 140 км/ч, длина пробега после посадки (L) оставляет 450 м. Найдите время (t) пробега и ускорение (a_пос).

Решение. Для определения ускорения самолета используем уравнение равнопеременного прямолинейного движения точки:

V = V₀ – a_t.

Так как в конце пробега самолет останавливается, то его конечная скорость обращается в нуль

0 = V₀ – a_t  .

; ,

отсюда

t = = 23,1 с.

V₀ = V_пос = 140/3,6 м/с; = V₀/t = 1,68 м/с².

Пример 2. Самолет при взлете, разбегаясь по ВПП, движется в соответствии с уравнением S = 1,1t² – 0,001t³ и взлетает через 30 с. Определите ускорения самолета в начальный момент (а₀) и в момент отрыва (а_отр), скорость отрыва (V_отр) и длину разбега (L).

Решение. Скорость движения точки равна первой производной от расстояния по времени:

V = dS/dt; V = 2,2t – 0,003t².

Ускорение прямолинейного движения (когда отсутствует нормальное ускорение) равно производной от скорости точки по времени:

= dV/dt; a = 2,2 – 0,006t.

Отсюда найдем ускорение в начальный момент (t = 0) и в момент отрыва (t_отр = 30 c):

= 2,2 м/с²; a_отр = 2,2 – 0,006· 30 = 2,02 м/с².

Определим скорость отрыва:

V = 2,2· 30 – 0,003· 30² = 63,3 м/с = 228 км/ч.

Найдем длину разбега:

L = 1,1· 30² – 0,001· 30³ = 963 м.