11. Линейные системы. Импульсный отклик линейной системы

Несмотря на то, что большинство процессов и явлений в окружающем нас мире имеют нелинейный характер, в физике, технике и математике широко используется понятия линейный сигнал, линейная система, линейное преобразование.

Рассмотрим некоторую систему, к входу которой приложено воздействие . На выходе системы формируется отклик (Рисунок 0 -3).

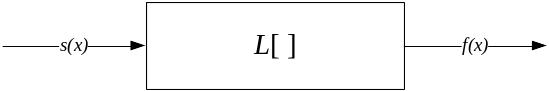
Рисунок 0‑3 – Схематичное обозначение системы

Преобразование, которое выполняет система над воздействием можно обозначить как оператор . В этом случае связь между функциями и задаётся в виде операторного уравнения

.

При этом говорят, что функция формируется в результате воздействия оператора на функцию .

Если для оператора выполняется принцип суперпозиции, то и сам оператор и соответствующая ему система называются линейными. Суть принципа суперпозиции можно выразить при помощи следующего соотношения

,

Импульсный отклик линейной системы

Выразим сигнал на входе рассматриваемой нами линейной системы через - функцию.

Используя полученное выражение для функции , запишем отклик системы

Оператор и операция интегрирования линейны, поэтому мы имеем право поменять их местами. В этом случае

,

или

.

Функция

называется импульсным откликом линейной системы.

Если импульсный отклик линейной системы известен, то вычисление отклика системы на заданное входное воздействие превращается в достаточно простую задачу – вычисление определенного интеграла.

Для сравнения рассмотрим пример, в котором линейная система описывается при помощи линейного интегрально-дифференциального уравнения. В качестве линейной системы возьмем обычную RLC цепочку.

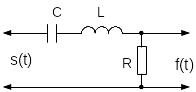
Рисунок 0‑4 – RLC-цепочка как пример линейной системы

Соотношение между входным и выходным сигналами описывается при помощи следующих уравнений.

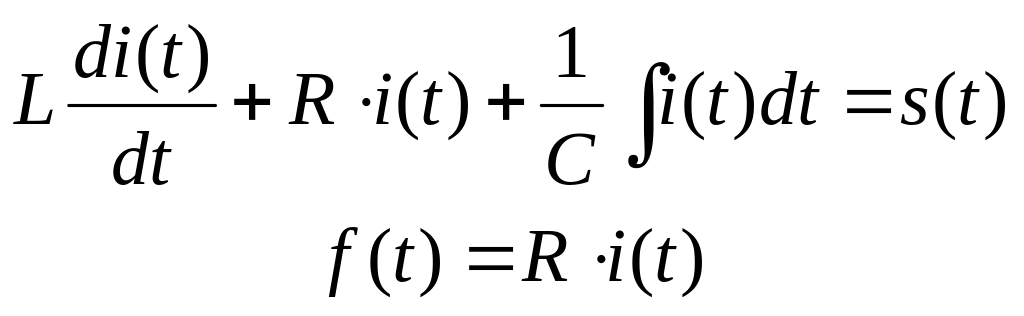
Пусть входным воздействием является очень короткий импульс напряжения, поступивший в момент времени : . Решая уравнения , можно получить, что выходной сигнал в этом случае будет описываться выражением

, где

Таким образом, выходной сигнал системы при подаче произвольного входного сигнала будет определяться как

.

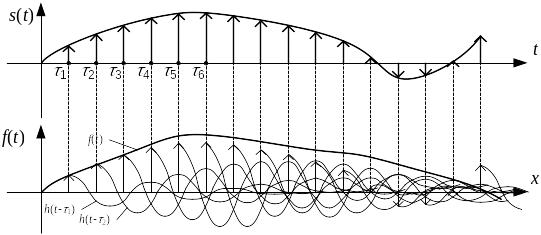
Наглядное представление преобразования сигналов RLC-цепочкой показано на следующем рисунке:

12. Прямые и обратные задачи. Уравнение Фредгольма

Выше нами получено соотношение, которое связывает между собой входное воздействие , отклик и функцию , которая описывает параметры системы. Одна из этих функций всегда неизвестна. В противном случае задача теряет смысл.

Прямые и обратные задачи.

В соответствии с терминологией, принятой в электродинамике и математической физике, определение отклика системы по входному воздействию при известной функции называется прямой задачей. Определение входного воздействия по отклику системы называется обратной задачей. И наконец, определение импульсного отклика системы по известным функциям и , называется задачей идентификации системы.

Очевидно, что решение прямой задачи сводится к вычислению определённого интеграла и является относительно простой задачей. Эта задача всегда имеет решение. Другой разговор, как быстро и с какой точностью его можно получить.

Решение обратных задач представляет собой значительно более сложную проблему. На сегодняшний день имеются различные подходы к её решению. Некоторые из них мы рассмотрим в рамках этого курса.

Начнём с чисто математических вопросов. В том случае, когда неизвестной функцией является входное воздействие, соотношение (9.1) превращается в интегральное уравнение (неизвестная функция находится под знаком интеграла)

Приведенное выше уравнение хорошо известно математикам и называется уравнением Фредгольма 1-го рода.

Определение входного воздействия по известному отклику системы носит название обратной задачи. Для решения обратной задачи необходимо решить интегральное уравнение (9.1), т.е. определить при известных функциях и функцию

Ядро интегрального уравнения.

Функция , которую мы знаем как импульсный отклик линейной системы или как аппаратную функцию, в теории интегральных уравнений носит название ядра интегрального уравнения.

Уравнения Фредгольма классифицируются по типу ядра. Если , то ядро называется симметричным, а уравнение Фредгольма соответственно уравнением Фредгольма с симметричным ядром.

Если , то ядро называется разностным. Линейные системы, которые описываются интегральным уравнением Фредгольма с разностным ядром, являются инвариантными к сдвигу.

В зависимости от типа ядра возможны те или иные методы решения уравнения Фредгольма. Наиболее простое решение имеет уравнение Фредгольма с разностным ядром. Несколько позже мы получим это решение.

Наиболее сложное решение имеют уравнения, ядра которых не относятся ни к симметричным, ни к разностным ядрам. В каждом конкретном случае для таких уравнений необходимо находить индивидуальное решение.

Собственные функциями интегрального уравнения.

Функции , удовлетворяющие равенству

называются собственными функциями интегрального уравнения, а числа его собственными значениями. Обычно собственными значения располагают в порядке убывания их абсолютной величины и числу с максимальным значением присваивают индекс равный 0. Собственные функции интегрального уравнения ортогональны если

.

Собственные функции интегральных уравнений Фредгольма с разностным и симметричным ядрами всегда можно привести к ортогональному виду.