Свойства дельта-функции
Фильтрующее свойство дельта-функции
Доказательство этого свойства тривиально.
Достаточно использовать подстановку
.
Дельта-функция со сложным аргументом
Определим значение следующего выражения
.
Для этого воспользуемся подстановкой
,
где
функция обратная
.
В результате получим
П
усть
монотонно возрастает на интервале
и имеет на этом интервале единственный
корень в точке
.
Т.е.
.
При этом
.
В этом случае согласно фильтрующему
свойству
.
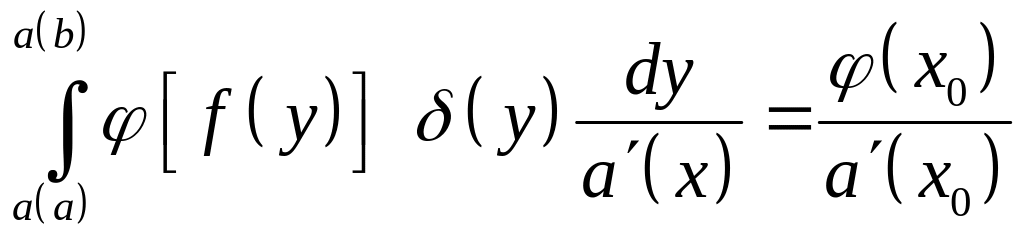Если
-
монотонно убывающая функция, то,
во-первых,
и во-вторых
т.е. нижний предел интегрирования в
полученном интеграле больше верхнего.
В то же самое время в определении
дельта-функции верхний предел
интегрирования больше нижнего. С учётом
этого после элементарных преобразований
получим
.
Очевидно, что последнее выражение справедливо как для случая монотонно убывающей, так и для случая монотонно возрастающёй функции .
Сравнивая полученное выражение с выражением для фильтрующего свойства, можно получить, что
,
где
корень функции
на интервале
.
Если функция
имеет не один, а счетное число корней,
то интервал интегрирования
разобьем на ряд интервалов
таких, что на каждом из них функция
имеет всего один корень
.
Выполнив для каждого интервала
выкладки, приведенные выше, получим
,
где
- корень уравнения
Наглядно дельта-функция сложного аргумента показана на рисунке 0 -2.
Рисунок 0‑2 – Дельта-функция сложного агрумента
Примеры
Рассмотрим несколько примеров. Первый – дельта-функция от линейной функции
,
где c – константа.
Второй пример - дельта функция от
.
Корни функции
равны
,
производная равна
.
С учётом этого получим
.
И последний пример, дельта-функция от
.
Функции
имеет
два корня 1 и –1, а производная равна 2x.
В итоге имеем
Преобразование Фурье. Теорема о свёртке
Преобразование Фурье – одно из наиболее часто используемых интегральных преобразований. По определению интегральное преобразование вида
называется интегральным преобразованием
Фурье функции
.
Для существования интегрального преобразования Фурье функция должна удовлетворять определённым условиям, которые называются условиями Дирихле. Условия Дирихле требуют, что бы функция была квадратично интегрируемой, имела конечное число разрывов первого рода и не имела разрывов второго рода. Это достаточно жёсткие условия. На практике они часто не соблюдаются и класс функций, для которых вычисляется преобразование Фурье, значительно шире класса функций, определяемого этими условиями.
Преобразование Фурье обратимо. Интегральное преобразование вида
называется обратным преобразованием
Фурье. Коэффициент
,
стоящий перед интегралом в этом выражении,
является нормирующим коэффициентом.
Он обеспечивает сохранение энергии при
последовательном выполнении прямого
и обратного преобразований Фурье.
Теорема о свёртке
Сверткой функций
и
называется
функция
Пусть для функций
,
и
существуют
преобразования Фурье соответственно
функции
,
и
.
Тогда
.
Т.е. спектр свёртки равен произведению спектров сворачиваемых функций.
Докажем эту теорему. По определению преобразования Фурье
.
Подставим вместо выражение этой функции через свёртку функций и . В результате получим
.
Преобразуем это выражение.
Так как пределы интегрирования бесконечны, можно разделить двойной интеграл в правой части этого выражения на два независимых интеграла. В результате получим то, что и требовалось доказать
.