42. Синтез апертуры сканирования двумя антеннами

Еще одним случаем синтеза апертуры является сканирование двумя антеннами. В этом случае при синтезе приемная и передающая антенны перемещаются синхронно относительно объекта. Схема синтеза апертуры сканированием двумя антеннами представлена на рисунке 15.

Рисунок 0.15 – Синтез апертуры сканированием двумя антеннами

Как и при сканировании передающей антенной, поле на поверхности объекта непостоянно, что не дает возможности непосредственно использовать приближение Кирхгофа и алгоритмы восстановления, описанные выше.

При синтезе апертуры сканированием двумя антеннами координаты перемещающихся антенн связаны выражениями

.

В результате эксперимента формируется некоторое пространственное распределение комплексной амплитуды поля. Следует отметить, что как и при синтезе апертуры сканированием передающей антенной, эти данные не описывают реальное распределение амплитуды и фазы поля в плоскости апертуры, поскольку в действительности поле на поверхности объекта переменно.

Будем считать передающую антенну точечным источником, излучающим сферическую волну. При нахождении передающей антенны в точке (x₀, y₀) комплексная амплитуда отраженного поля на поверхности объекта равна

.

Поле, рассеянное объектом в плоскость апертуры, будет описываться выражением

.

Выше было показано, что при использовании приближения Френеля свертка вида приобретает вид

.

Подставим соотношение в выражение , в результате чего получим

.

Предположим, что антенны расположены достаточно близко друг от друга, и расстоянием между ними можно пренебречь; в этом случае R₀ ≈ R_a. Кроме того, с учетом приближения Френеля R₀ ≈ z. Учитывая эти допущения можно записать, что

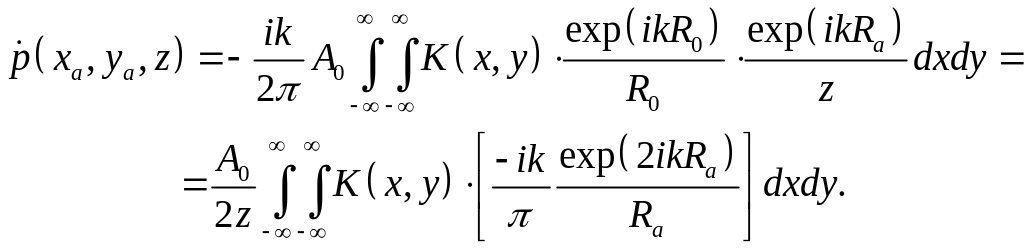
Видно, что с учетом некоторых приближений, формируемое при синтезе апертуры сканированием двумя антеннами поле представляет собой свертку коэффициента отражения объекта и величины

,

которую можно трактовать как импульсный отклик свободного пространства в приближении Френеля для поля с частотой, в два раза большей истинной частоты облучения.

Такой вывод позволяет использовать для восстановления объекта известные алгоритмы, считая, что снятое при эксперименте с синтезом апертуры сканированием двумя антеннами распределение является распределением поля в плоскости апертуры, а частота поля в два раза больше действительной частоты облучения.

Азимутальное разрешение такой голографической системы будет определяться выражением, аналогичным с учетом того, что функция рассеяния системы записывается для удвоенной частоты поля:

.

Таким образом, разрешающая способность системы в этом случае в два раза выше, чем при синтезе апертуры сканированием одной антенной.

Дополнительной разновидностью способа синтеза апертуры сканированием двумя антеннами является сканирование объектом. В этом случае приемная и передающая антенны неподвижны, а при синтезе апертуры перемещается сам объект. Формируемое распределение поля в этом случае определяется координатами объекта.

Очевидно, что синтез апертуры сканированием объектом аналогичен синтезу сканированием двумя антеннами, за исключением того, что формируемое изображение объекта зеркально развернуто относительно обеих координатных осей.