32. Работа по перемещению заряда в электростатическом поле. Циркуляция вектора

Рис. 32.1

Найдём элементарную работу по перемещению заряда q в поле, создаваемом зарядом Q:

dA=Fdl cos .

где  — угол между силой и направлением перемещения .

Из рис. 32.1 видно, что dl cos  = dr, поэтому

dA=Fdr.

(32.1)

Суммарную работу по перемещению заряда из точки А в точку В найдём интегрированием выражения (32.1). Используя закон Кулона, получаем

.

(32.2)

Если заряд перемещается из точки А в точку В по другому пути (пунктирная линия на рис.32.1), то проделав такие же выкладки, снова придём к формуле (32.2). Следовательно, работа в электростатическом поле не зависит от формы пути, а зависит лишь от выбора начальной и конечной точки. Кроме того, как видно из (32.2), работа по перемещению заряда в электростатическом поле по замкнутому контуру равна нулю, т.е.

;

(32.3)

.

(32.4)

Формула (32.4) получается из (32.3) подстановкой: F=qE.

Интеграл, фигурирующий в (32.4), называется циркуляцией напряжённости электростатического поля. Видно, что циркуляция вектора равна нулю.

Эти признаки означают, что электростатическое поле является потенциальным. В соответствии с результатом, полученным в §3, работу потенциальных (консервативных) сил можно выразить через разность потенциальных энергий. Из сопоставления (3.6) и (32.2) заключаем, что потенциальная энергия взаимодействия двух точечных зарядов

.

(32.5)

Введем теперь энергетическую характеристику электростатического поля — потенциал. Потенциалом называется скалярная величина, численно равная потенциальной энергии единичного положительного заряда, помещённого в данную точку поля:

.

(32.6)

Потенциал измеряется в вольтах: один вольт — это потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией в 1 Дж.

Потенциал поля точечного заряда найдём, подставив (32.5) в (32.6):

.

(32.7)

И, наконец, подставив (32.6) в (3.6), выражение для работы по перемещению заряда в электростатическом поле из одной точки в другую можно представить как произведение заряда на разность потенциалов:

.

(32.8)

33. Связь между напряжённостью поля и потенциалом

Эквипотенциальной поверхностью называется поверхность, в каждой точке которой значение потенциала одно и то же: =const.

Найдём элементарную работу по перемещению заряда q на участке пути dl, лежащем на эквипотенциальной поверхности: dA=qd=0, поскольку =const и, следовательно, d=0. С другой стороны, dA=qEdlcos. Учитывая предыдущий результат, находим qEdlcos=0, т.е. cos=0, =/2.

Таким образом, силовые линии перпендикулярны эквипотенциальной поверхности.

Найдём теперь работу по перемещению заряда q с одной эквипотенциальной поверхности с потенциалом  на другую — с потенциалом  + d, передвигая заряд вдоль силовой линии — рис. 33.1. С одной стороны,

Рис. 33.1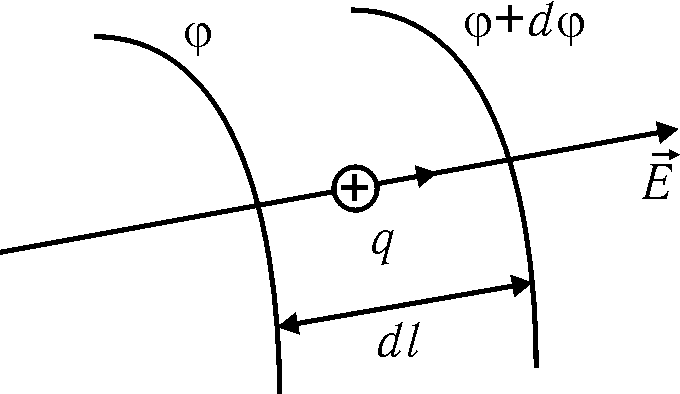

dA=q – ( + d) = –qd,

с другой стороны, используя силовую характеристику поля — напряжённость E, получим:

dA=Fdl=qEdl.

Приравнивая правые части, получим:

qEdl = -qd; Edl = -d.

Отсюда

.

(33.1)

или

.

(33.2)

Формула (33.1) даёт возможность рассчитать напряжённость поля, если известно распределение потенциала в пространстве. Выражение называется градиентом потенциала. Знак "–" указывает, что вектор напряжённости направлен в сторону убыли потенциала.

Формула (33.2) позволяет найти потенциал по известной зависимости Е от пространственных координат. Приведём примеры.

1. Поле точечного заряда:

.

(33.3)

2. Поле плоского конденсатора:

,

(33.4)

где d — расстояние между обкладками конденсатора.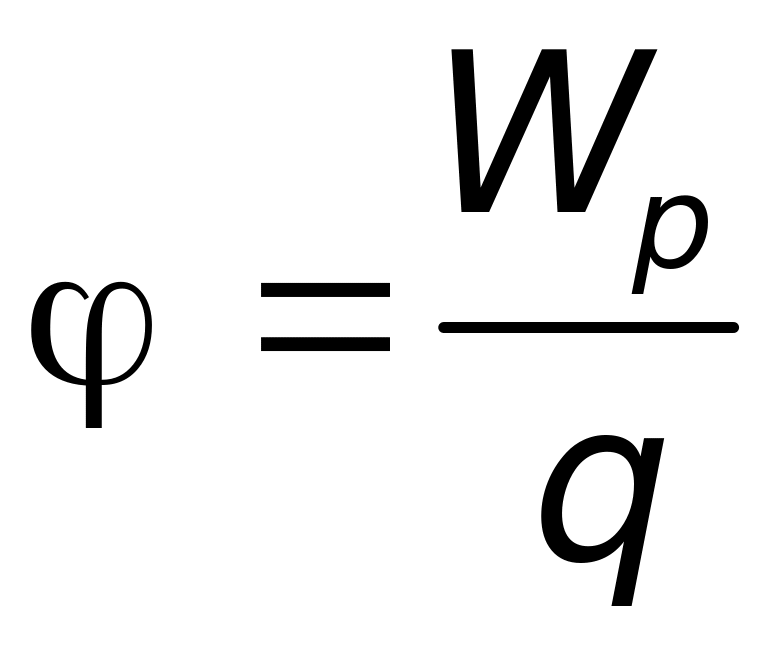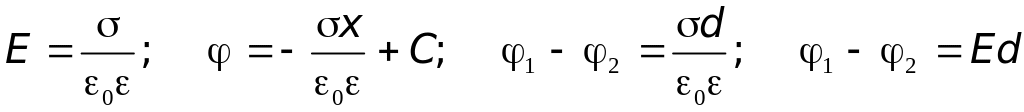