II. Механические колебания и волны
5. Общая характеристика колебательных процессов. Гармонические колебания
Колебаниями называются движения или процессы, обладающие той или иной степенью повторяемости во времени.
В технике устройства, использующие колебательные процессы могут выполнять определённые функциональные обязанности (маятник, колебательный контур, генератор колебаний и др.), а также могут возникать как неизбежное проявление физических свойств (вибрация машин и механизмов, неустойчивости и колебательные потоки при движении тел в жидкостях и газах и т.п.).
Колебания называются периодическими, если система через определенные равные промежутки времени, называемые периодом колебаний, проходит через одни и те же состояния. Такие колебания описываются периодическими функциями от времени
x(t)=x(t+T),
где x — смещение (отклонение от положения равновесия) в момент времени t, Т — период колебаний, равный времени совершения одного полного колебания.
Рис.
5.1
Особенно важную роль в физике играют гармонические колебания, в которых зависимость смещения от времени описывается гармоническим законом
x=Acos(0t+0) |
(5.1) |
или
x=Asin(0t+0) |
(5.2) |
Здесь A — амплитуда колебаний, т.е. максимальное по модулю смещение от положения равновесия; 0 — циклическая (или круговая) частота колебаний, равная числу полных колебаний, совершаемых за время 2 секунд. Удобно также характеризовать периодические колебания линейной частотой , которая равна числу полных колебаний, совершаемых за 1 с. Единица линейной частоты 1 герц (Гц) — частота такого колебательного движения, в котором за 1 с совершается одно полное колебание.
В формулах (5.1) и (5.2) аргумент тригонометрической функции представляет собой фазу. Фаза показывает, какая часть колебания выполнена к данному моменту времени, если полному колебанию сопоставить значение 2. Обычно выделяют текущую фазу — 0t, значение которой изменяется со временем, и начальную фазу 0, определяющую смещение в начальный момент времени (t=0).
Исходя из (5.1), можно получить выражения для скорости и ускорения при гармоническом колебании:
|
(5.3) |
Из (5.3) следует уравнение гармонических колебаний в дифференциальной форме:
|
(5.4) |
.6. Колебания пружинного маятника
Рис. 6.1
При смещении тела на величину x от положения равновесия возникает упругая сила
F=-kx, |
(6.1) |
которая стремится вернуть тело в положение равновесия. Если отпустить тело, то под действием этой силы оно начнёт двигаться.
Для нахождения уравнения движения воспользуемся вторым законом Ньютона
|
(6.2) |
.
Сравнивая (6.2) и (5.4), видим, что пружинный маятник совершает гармонические колебания с частотой
|
(6.3) |
.
Период колебаний пружинного маятника
|
(6.4) |
.Многие силы, не являющиеся упругими по своей природе, также могут удовлетворять соотношению (6.1). Такие силы объединены под общим названием квазиупругих. Квазиупругая сила пропорциональна смещению от положения равновесия и всегда направлена к положению равновесия. При этом параметр k в (6.1) называют квазиупругой постоянной.
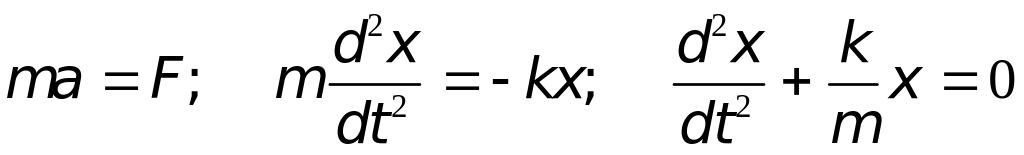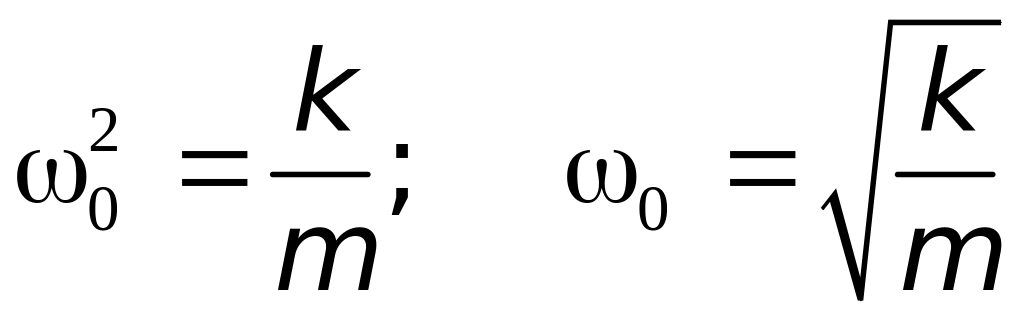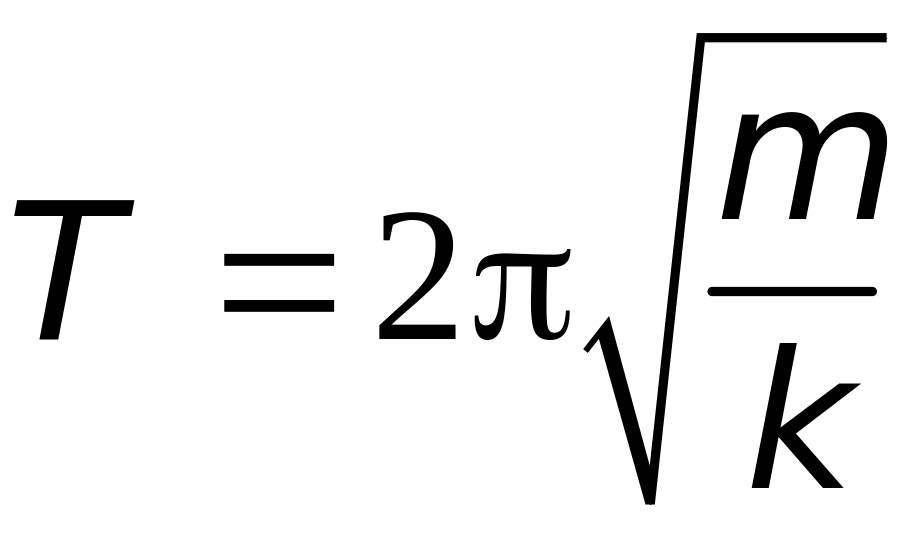