30. Силовые линии. Поток вектора . Теорема Остроградского-Гаусса

Силовой линией электростатического поля называется линия, касательная к которой в каждой точке совпадает с направлением вектора (рис. 30.1,а).

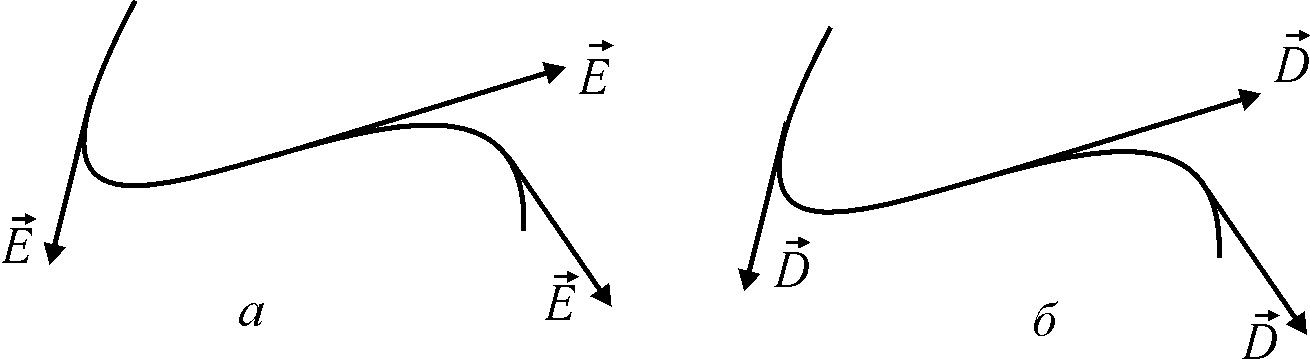
Рис. 30.1

Свойства силовых линий;

а) силовые линии электростатического поля не пересекаются;

б) силовые линии электростатического поля разомкнуты — они начинаются на положительных зарядах и заканчиваются на отрицательных (или уходят в бесконечность).

Аналогично вводится понятие линии электрического смещения — рис. 30.1,б.

Элементарный поток вектора электрического смещения через площадку dS вводится как произведение

dФe=DdScos,

(30.1)

где  — угол между вектором и нормалью к площадке — рис. 30.2.

Рис. 30.2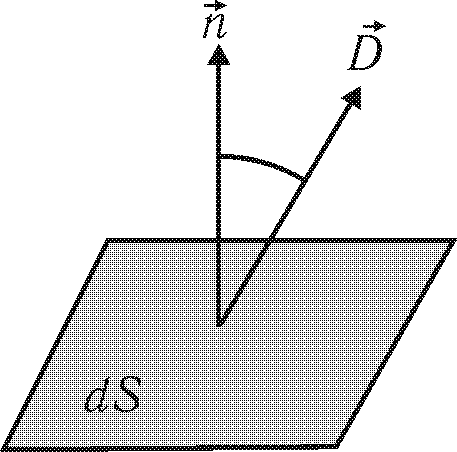

Суммарный поток вектора через какую-либо поверхность можно найти интегрированием (30.1) по всей поверхности

;

для замкнутой поверхности

.

Важнейшую роль в электростатике играет теорема Остроградского-Гаусса: поток вектора электрического смещения через любую замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности:

.

Доказательство теоремы проведём для простейшего случая, когда замкнутая поверхность представляет собой сферу, в центре которой находится точечный заряд Q.

Рис. 30.3

Выделим на поверхности сферы элементарную площадку dS — рис. 30.3.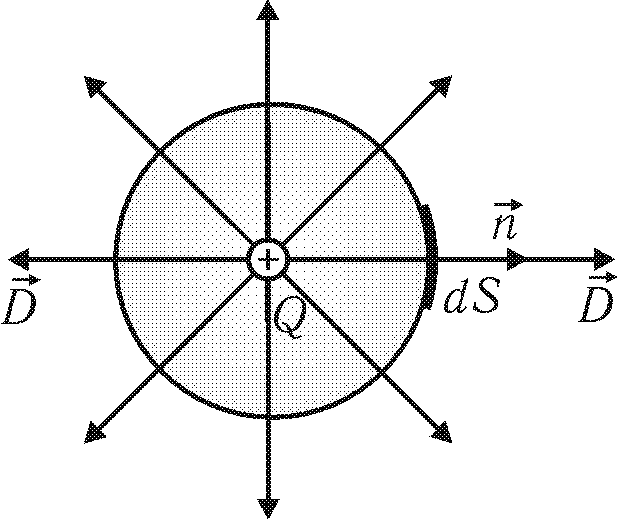

Нормаль к этой поверхности и вектор совпадают по направлению, поэтому

.

Используя далее формулу (29.5), получим

.

Теорема доказана.

В суммарном потоке, который создают заряды, расположенные за пределами замкнутой поверхности, можно выделить положительную и отрицательную части, которые взаимно компенсируются. Поэтому внешние по отношению к данной замкнутой поверхности заряды в теореме Остроградского-Гаусса не учитываются.

Теорема Остроградского-Гаусса связывает заряды с создаваемыми ими электростатическими полями и отражает тот факт, что источником электростатического поля являются электрические заряды.

31. Применения теоремы Остроградского-Гаусса для расчёта полей

Теорема Остроградского-Гаусса в ряде случае позволяет сравнительно просто рассчитать напряжённость электростатического поля при заданном распределении зарядов. Рассмотрим несколько примеров.

1. Поле равномерно заряженной плоскости.

Рис. 31.1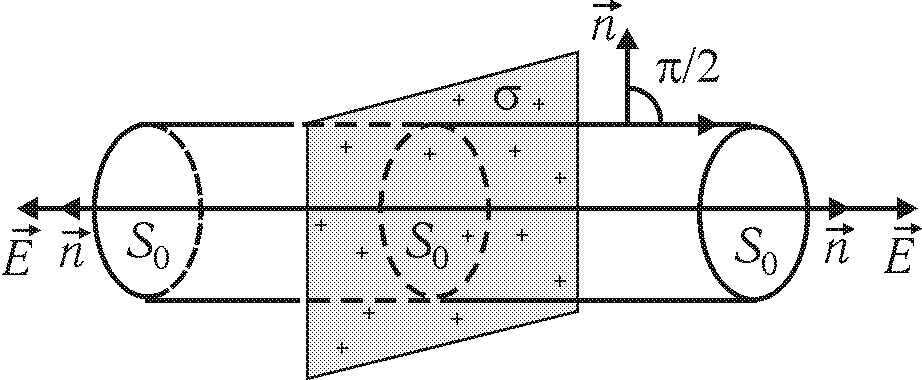

Пусть имеется бесконечная равномерно заряженная плоскость (рис. 31.1) с поверхностной плотностью заряда =Q/S Кл/м².

Суммарный поток вектора , очевидно, составляет:

Ф_е=Ф_бок+2Ф_осн

Поток через боковую поверхность равен нулю, так как  :

Ф_бок=DS_бокcos/2=0.

Поток через основание цилиндра:

Ф_осн=DS_оснcos0=DS_осн.

Таким образом, полный поток вектора через замкнутую поверхность Ф_е=2 DS_осн.

По теореме Остроградского-Гаусса 2DS_осн=Q=S_осн. Отсюда

.

(31.1)

2. Поле двух бесконечных равномерно заряженных плоскостей. Рассчитаем напряжённость поля, создаваемого двумя бесконечными параллельными плоскостями, равномерно заряженными с поверхностной плотностью заряда + и – (рис. 31.2).

Согласно принципу суперпозиции суммарная напряжённость поля

,

Рис. 31.2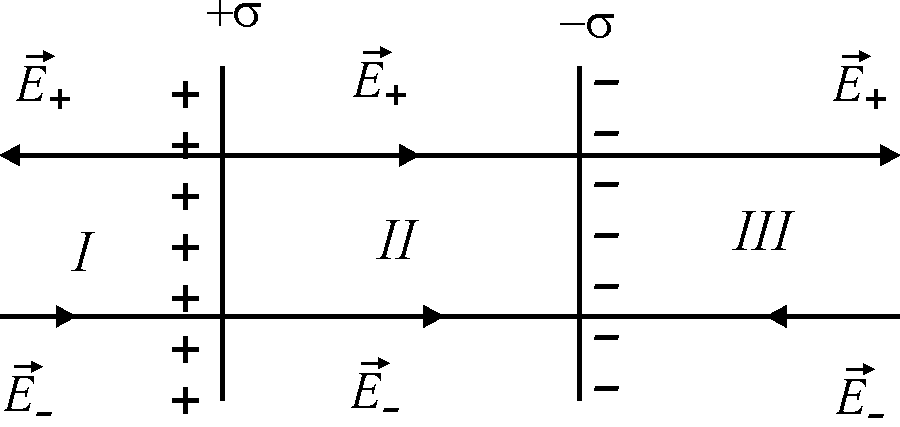

где и — напряженности поля, создаваемого соответственно положительно и отрицательно заряженными плоскостями.

В областях пространства I и III (рис. 31.2) векторы и направлены в противоположные стороны, поэтому суммарная напряжённость .

В области II векторы и параллельны и равны по модулю, поэтому E=2E₊. Используя предыдущий результат (31.1), получим:

.

(31.2)
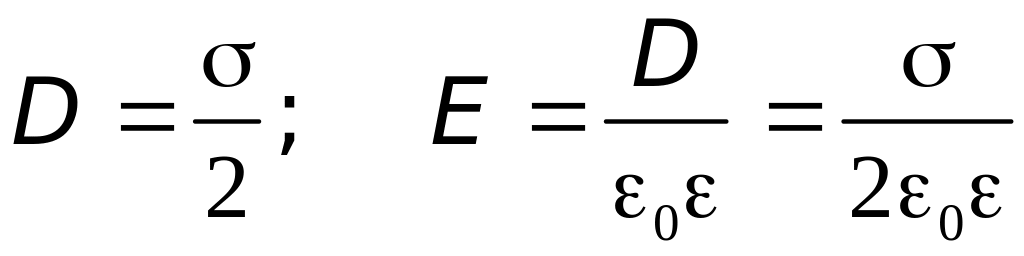