7. Энергия гармонического колебания

Рассмотрим теперь на примере пружинного маятника процессы изменения энергии в гармоническом колебании.

Очевидно, что полная энергия пружинного маятника W=W_k+W_p, где кинетическая W_k и потенциальная W_p энергии определяются выражениями

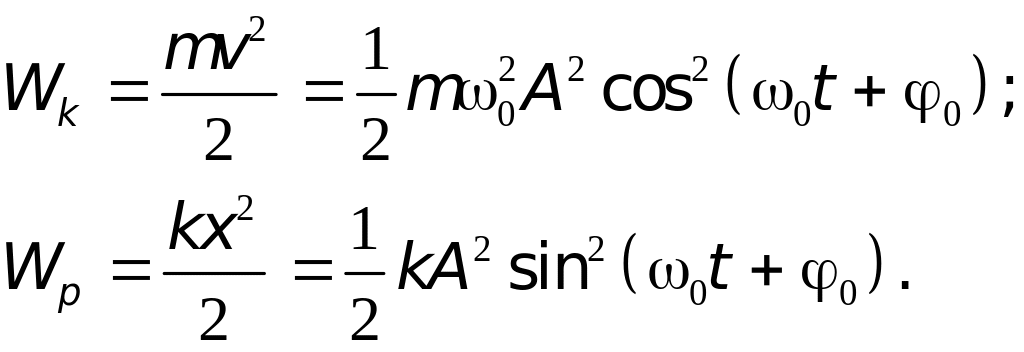
Поскольку , то выражение для потенциальной энергии можно представить в виде

.

Рис. 7.1

Зависимости от времени кинетической и потенциальной энергии гармонических колебаний показаны на рис. 7.1.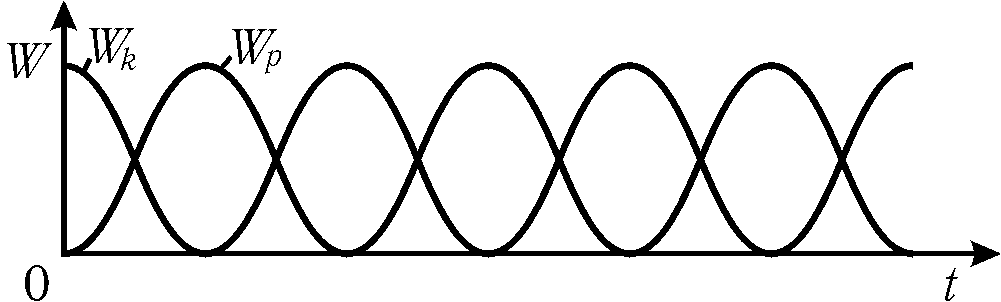

Полная энергия гармонического колебания

(7.1)

не зависит от времени.

8. Сложение гармонических колебаний одинакового направления

Решение ряда вопросов, в частности, сложение нескольких колебаний одинакового направления, значительно облегчается, если изображать колебания графически, в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой.

Рис. 8.1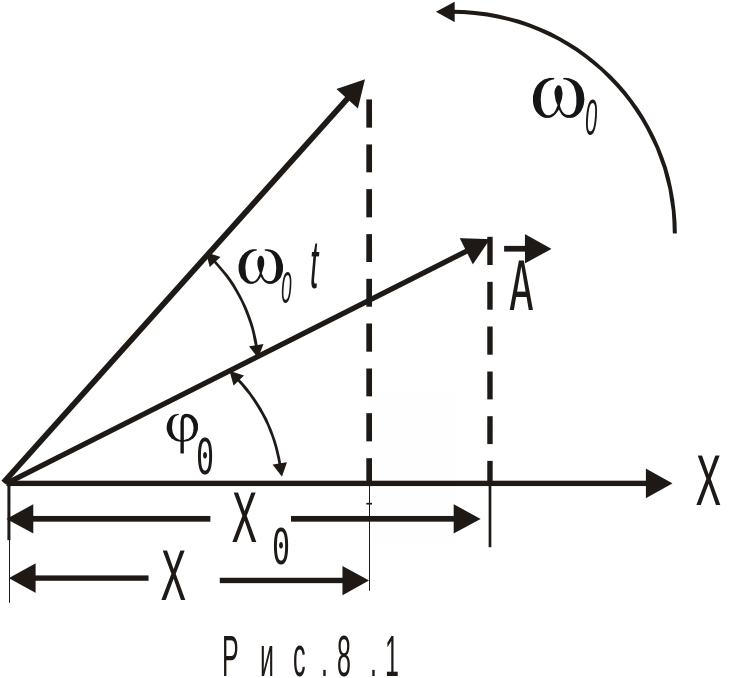

Из точки O, взятой на оси x построим вектор , образующий с осью угол ₀ (рис. 8.1).

Проекция этого вектора на ось x равна

x=Acos₀.

Предположим теперь, что вектор равномерно вращается с угловой скоростью ₀. Тогда за время t он опишет угол, равный ₀t, и новая проекция этого вектора на ось х станет равной:

x=Acos (₀t+₀).

Следовательно, проекция конца вектора на ось x будет совершать гармонические колебания с амплитудой, равной длине вектора , с частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью x в начальный момент времени. Из сказанного следует, что гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью x угол, равный начальной фазе колебаний.

Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты:

x₁=A₁ cos(₀t+₁); x₂=A₂ cos(₀t+₂).

Представим оба колебания с помощью векторов ₁ и ₂, образующих с осью х углы ₁ и ₂ соответственно (рис. 8.2). Построим по правилу сложения векторов результирующий вектор _p. Легко видеть, что проекция этого вектора на ось х равна сумме:

x=x₁ + x₂.

Рис. 8.2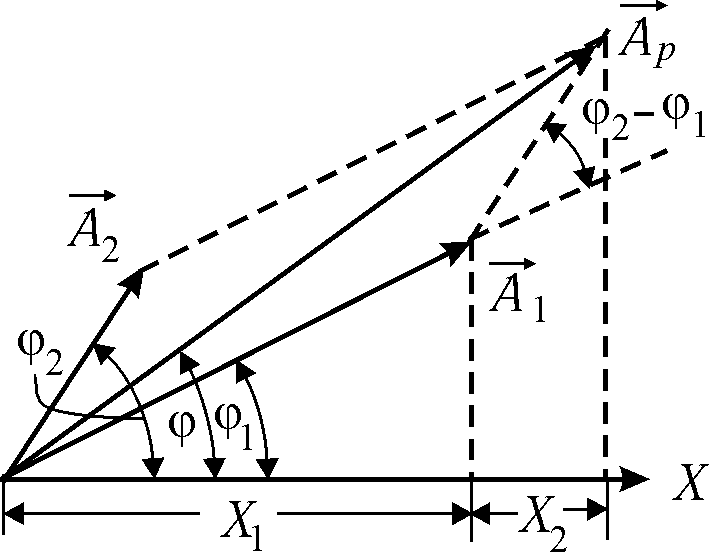

Вектор _p вращается с той же угловой скоростью, как и векторы ₁ и ₂, так что результирующее движение будет гармоническим колебанием с частотой ₀, амплитудой А_p и начальной фазой :

X=A_p cos(₀t+).

Найдём теперь из векторной диаграммы результирующую амплитуду. По теореме косинусов имеем:

.

(8.1)

Упражнение. Рассмотрите, чему будет равна результирующая амплитуда колебаний, если: a) ₂ - ₁ = 0; б) ₂ - ₁ = .

9. Затухающие колебания

В реальных условиях в системах, совершающих колебания, всегда присутствуют силы сопротивления. В результате система постепенно расходует свою энергию на выполнение работы против сил сопротивления и колебания, в конце концов, прекращаются.

Рис. 9.1

Рассмотрим случай, когда колеблющееся тело находится в вязкой среде, а его скорость v невелика — рис. 9.1.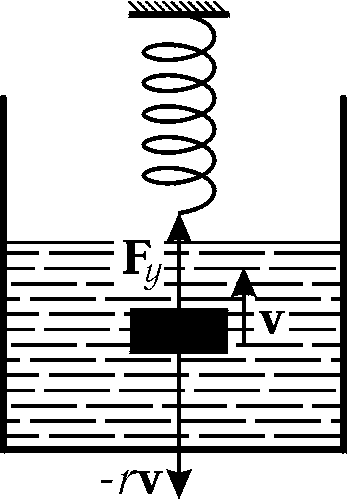

Тогда на тело действует сила сопротивления, равная

,

(9.1)

где r — коэффициент сопротивления, зависящий от формы тела и вязкости среды.

Результирующая сила, действующая на тело, равна сумме квазиупругой силы и силы сопротивления:

.

Составим уравнение движения, используя второй закон Ньютона:

.

Замечая, что , получим:

.

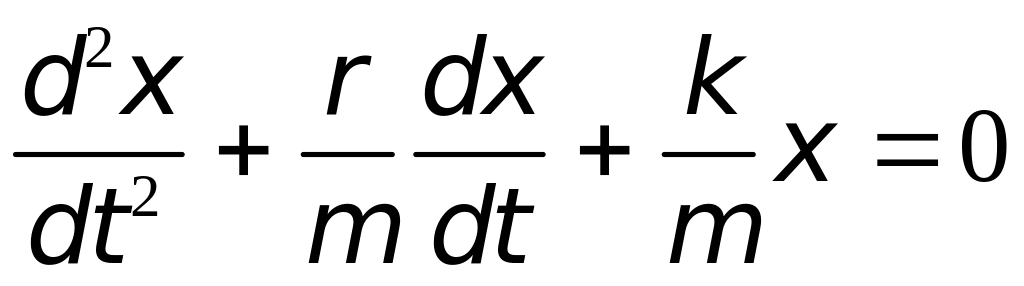Последнее уравнение представляет собой дифференциальное уравнение затухающих колебаний, которое обычно представляют в виде:

,

(9.2)

где =r/2m — коэффициент затухания, а — циклическая частота собственных свободных колебаний той же системы при  = 0.

Если пренебречь силами трения (т.е. положить  = 0), то уравнение (9.2) переходит в уравнение гармонических колебаний (5.4), решение которого имеет вид x=A cos(₀t + ), где A=const.

Если же 0, но не слишком велико (т.е. ), то зависимость, удовлетворяющая уравнению (9.2), имеет вид:

x(t) = A(t) cos(t + ).

(9.3)

Здесь  — циклическая частота затухающих колебаний, которая связана с частотой незатухающих (гармонических) колебаний соотношением:

.

(9.4)

Амплитуда затухающих колебаний экспоненциально убывает с течением времени:

.

(9.5)

Зависимости x(t) и A(t) показаны на рис. 9.2.

Рис. 9.2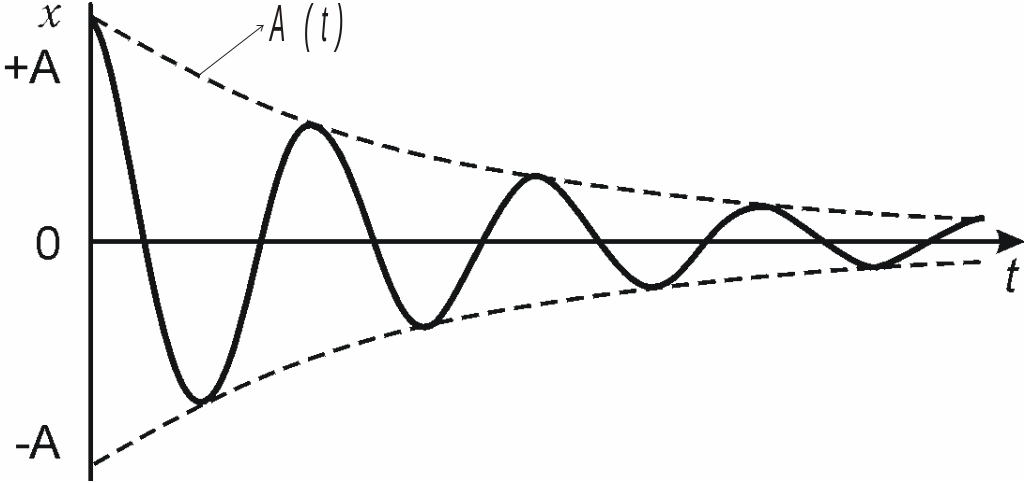

Введём некоторые характеристики затухающих колебаний.

Логарифмический декремент затухания численно равен натуральному логарифму отношения значений амплитуд затухающих колебаний в моменты времени t и t+T:

.

(9.6)

Подставим (9.5) в (9.6):

.

(9.7)

Логарифмический декремент затухания характеризует скорость затухания: чем больше , тем быстрее затухают колебания.

Добротность колебательной системы определяется формулой

.

(9.8)

где W(t) — энергия колебаний в момент времени t. Чем больше добротность системы, тем дольше сохраняются колебания. При малых значениях логарифмического декремента затухания справедлива формула: .
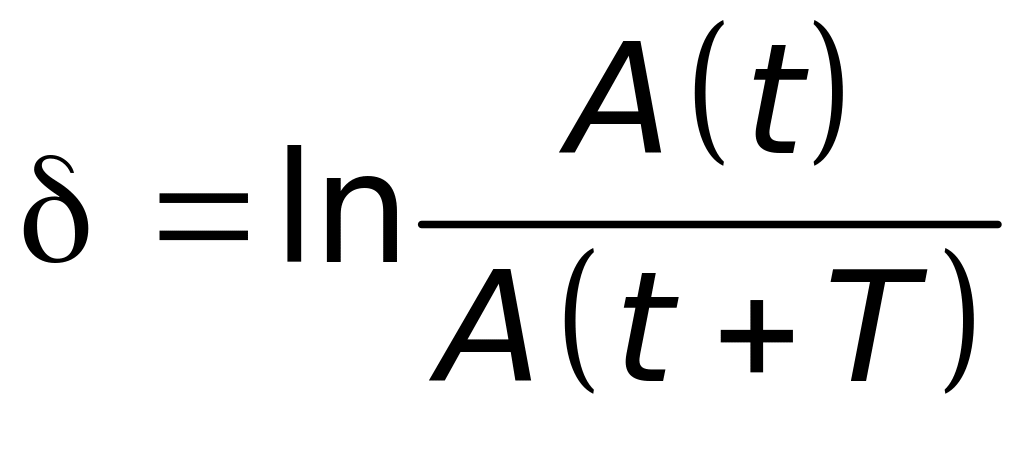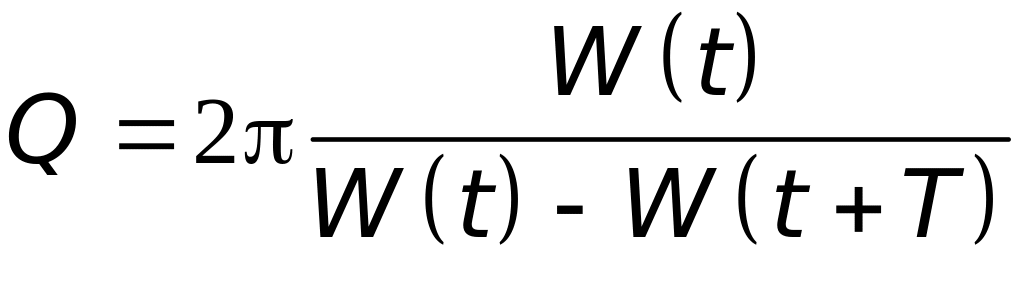