1. Рассчитать напряженность поля прямой бесконечной нити, равномерно заряженной с линейной плотностью , в точке о, удаленной на расстояние r0.

Решение. Заряд нити неточечный, поэтому непосредственно использовать формулу (3.13) нельзя. Применим сначала теорему Гаусса. В силу симметрии поля вектор напряженности в любой точке нормален цилиндрической поверхности, проходящей через эту точку. Ось симметрии этой поверхности совпадает с нитью. Поэтому в качестве замкнутой поверхности выберем цилиндр длиной l с осью симметрии, совпадающей с нитью, боковая поверхность которого проходит через точку О (рис. 3.4). Поток вектора через боковую поверхность цилиндра , а электрический заряд, расположенный внутри цилиндра, . По теореме Гаусса, .

Отсюда определяем искомую напряженность:

. (3.15)

Попробуем применить метод ДИ. Разделим нить на столь малые элементы, чтобы заряд, находящийся на каждом таком элементе, был точечным. Рассмотрим один такой элемент длиной dl с зарядом dQ=τdl (рис. 3.5). В точке О элементарная напряженность поля этого заряда

. (3.16)

Из треугольника ADO находим .

Так как , то из треугольника АВС определяем

.

Подставляя значения r и dl в уравнение (3.16), получаем

. (3.17)

Проекции вектора на оси OX и OY:

, (3.18)

. (3.19)

Отсюда, после интегрирования получаем

.

Таким образом, окончательно , что совпадает с выражением (3.15), полученным с помощью теоремы Гаусса.

На первый взгляд метод ДИ при расчете поля нити оказался более трудоемким, чем использование теоремы Гаусса. В данном примере это действительно так. Но метод ДИ является универсальным, он может быть применен практически и в тех случаях, когда теорема Гаусса оказывается бесплодной.

2. Определить напряженность поля отрезка, равномерно заряженного с линейной плотностью заряда τ, в точке О, удаленной от отрезка на расстояние r₀. углы α₁ и α₂ заданы (рис. 3.6).

Решение. Легко видеть, что симметрия поля бесконечной нити нарушена, поле отрезка несимметрично. Очень трудно построить замкнутую поверхность, окружающую отрезок, для которой по теореме Гаусса можно было бы относительно просто вычислить поток вектора напряженности.

Применим метод ДИ. Проекция вектора dE элементарной напряженности на оси ОХ и OY получены в предыдущем примере. Интегрируя соотношения (3.18) и (3.19), находим проекции (компоненты) искомого вектора на оси ОХ и OY:

(3.20)

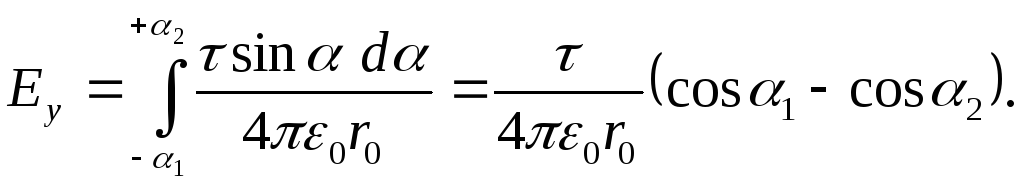(3.21)

Легко показать, что поле бесконечной нити (3.15) является частным случаем поля отрезка. Действительно, при и из (3.20) и (3.21) получаем и , что совпадает с (3.15).

2. Проводники в электрическом поле

Поверхность проводника является эквипотенциальной поверхностью. На этом свойстве проводников основан метод зеркальных изображений. Этот метод позволяет рассчитывать различные электростатические поля, определять емкость системы проводников и т.д.

Метод зеркальных изображений основан на следующем положении. Если в произвольном электростатическом поле заменить эквипотенциальную поверхность металлической поверхностью такой же формы и создать на ней такой же потенциал, то данное электростатическое поле не измениться.

Рассмотрим электрическое поле между точечным зарядом +Q и бесконечной металлической поверхностью, потенциал которой равен нулю. В силу выше сформулированного положения это поле эквивалентно электрическому полю, созданному данным точечным зарядом +Q и точечным зарядом –Q, являющимся зеркальным изображением данного заряда +Q в металлической плоскости (рис. 3.7).

3. Точечный заряд Q=+2·10^-8 Кл находится на расстоянии l=1 м от бесконечной металлической плоскости, отведенной к Земле (рис. 3.7). Определить силу взаимодействия между зарядом и плоскостью.

Решение. Металлическая плоскость находится в электрическом поле точечного заряда. Вследствие явления электростатической индукции на стороне металлической плоскости, ближайшей к точечному заряду, появляются наведенные электрические заряды противоположного знака. Поэтому возникает сила взаимодействия между данным точечным зарядом и зарядами, наведенными на плоскости. Потенциал плоскости по условию равен нулю (потенциал Земли условно принимают за нуль). Следовательно, согласно методу зеркального изображения, электрическое поле между точечным зарядом и плоскостью эквивалентно полю, созданному данным зарядом и его зеркальным изображением в металлической плоскости. По закону Кулона получаем искомую силу взаимодействия:

.