3. Поле тяготения при произвольном распределении масс

В этом случае для расчета поля тяготения используется принцип суперпозиции и метод ДИ. Применяя этот метод при расчете напряженности поля, очень важно учитывать векторный характер этой величины. После нахождения элементарного вектора напряженности определяют его проекции , , на соответствующие оси координат, а последующие интегрирование (суммирование) происходит для каждой проекции отдельно.

Если напряженность поля известна, то задачу на движение тел в таких полях решают или динамическим методом, или методом законов сохранения.

4. Описать движение материальной точки в поле тяготения длинного тонкого однородного стержня массой м и длиной l. Влиянием других тел пренебречь.

Р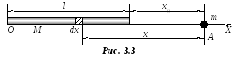ешение. Ограничимся решением одномерной задачи – предположим, что материальная точка в начальный момент времени находилась на оси стержня на расстоянии x₀=l от одного из его концов (точка А на рис. 3.3) и имела начальную скорость, равную нулю (v₀=0). Физическая система состоит из двух тел: стержня и материальной точки (обозначим ее массу т). Физическое явление заключается в движении материальной точки в поле тяготения стержня.

Сила тяготения, действующая на материальную точку, неизвестна (она не равна , ибо стержень не материальная точка). Для применения динамического метода необходимо рассчитать поле тяготения стержня на его оси, т.е. найти вектор напряженности и потенциал . Применим метод ДИ. Будем считать, что . Инерциальную систему отсчета свяжем со стержнем, начало координат поместим в левый конец стержня, а ось ОХ направим вправо. Разделим стержень на столь малые части, чтобы каждую из них можно было бы принять за материальную точку. Рассмотрим один такой элемент длиной dx, находящейся на расстоянии х от произвольной точки А на оси стержня. Его масса , где S – площадь сечения стержня, а плотность. Так как выделенный элемент – материальная точка, то характеристики его поля (напряженность dE и потенциал ) известны:

.

Заметим, что в нашем случае элементарные векторы напряженности, созданные всеми элементами стержня , направлены в одну сторону. После интегрирования получаем суммарные характеристики поля всех элементов стержня (т.е. поле стержня):

.

Сила, действующая на материальную точку, находящуюся на расстоянии х от начала координат,

.

По второму закону Ньютона

получаем дифференциальное уравнение, после решения которого можно было бы найти закон движения материальной точки.

Применяя закон сохранения энергии в механике

,

можно определить скорость движения материальной точки, находящейся на расстоянии х от правого конца стержня:

.

2. Электрическое поле

   1. Электрическое поле в вакууме

Фундаментальным законом электростатического поля является закон Кулона

. (3.12)

Он справедлив для точечных и неподвижных электрических зарядов. Закон Кулона по форме очень похож на закон всемирного тяготения Ньютона. Поэтому почти все, что было сказано в разделе 3.1 о поле тяготения, можно буквально повторить и для электростатического поля.

Основными характеристиками электростатического поля являются напряженность и потенциал . Для поля, созданного точечным зарядом,

, (3.13)

. (3.14)

Напряженность и потенциал связаны соотношением (3.6).

Состояние электростатического поля как физической системы определяется значением вектора напряженности в любой точке поле. Следовательно, основная задача электростатики заключается в расчете электростатического поля. Здесь полезно различать три случая:

2. поле создано системой точечных зарядов;

3. поле создано системой точечных и неточечных зарядов, расположенных на телах правильной геометрической формы;

4. поле создано произвольным распределением зарядов.

Хотя первый случай рассматривался в поле тяготения, весьма полезно рассчитать поле диполя. Во втором случае сначала по теореме Гаусса рассчитывают поля неточечных зарядов, а затем, используя принцип суперпозиции, определяют суммарное поле. При произвольном распределении зарядов используют метод ДИ.

Если характеристики поля будут рассчитаны, то задачи о движении заряженных частиц в известном поле можно решить или динамическим методом, или методом законов сохранения.