4. Законы сохранения

Кроме кинематического и динамического методов решения задач в физике существует еще один, может быть более важный и универсальный, метод применения законов сохранения. Если применение динамико-кинематического метода ограничено рамками только классических физических систем, то метод законов сохранения используется и в классических, и в квантовых системах.

Необходимо все же отметить, что в классических физических системах динамико-кинематический метод является более общим, чем метод законов сохранения. В особенности это относится к механическим системам. В принципе, любая поставленная механическая задача может быть решена с помощью динамико-кинематического метода. Этого нельзя утверждать относительно метода законов сохранения: далеко не все механические задачи решаются путем использования законов сохранения. Однако в более сложных системах метод законов сохранения иногда быстрее приводит к успеху, чем применение динамико-кинематического метода.

Как было отмечено выше, одного универсального способа (метода) решения задач по физике не существует. Огромное значение здесь имеет лишь система методов. Поэтому нет смысла противопоставлять один метод другому: каждый метод обладает и сильными и слабыми сторонами. Природа столь разнообразна в своих свойствах и проявлениях, что для раскрытия связей в физических системах необходимо разумное сочетание различных методов. Поэтому и при решении физических задач целесообразно использовать систему методов, в том числе и динамико-кинематический и метод законов сохранения.

В основе рассматриваемого метода лежит совокупность законов сохранения. В физике их довольно много. В классических системах используются следующие четыре: закон сохранения импульса, закон сохранения механической энергии, закон сохранения момента импульса и закон сохранения электрического заряда. Общим для всех этих законов является утверждение о сохранении какой-то физической величины при определенных условиях. Если обозначить эту неизменяющуюся величину через А, а набор условий, при которых выполняется утверждение закона, через В, то законы сохранения можно сформулировать в обобщенной форме: если выполняется В, то А=const; или в другом виде: если выполняется В, то ΔА=0, где ΔА – изменение величины А.

В большинстве случаев законы сохранения применяют, если происходит процесс взаимодействия тел. В этом процессе необходимо различать три этапа: первый характеризуется состоянием тел до их взаимодействия, второй есть сам процесс взаимодействия, и третий этап характеризуется состоянием тел после их взаимодействия. Процесс взаимодействия тел несущественен для законов сохранения. Для них важно только, чтобы значение соответствующей физической величины не изменялось в результате этого процесса (ее значения в начале и конце взаимодействия должны быть равны). Поэтому метод применения законов сохранения заключается в следующем:

4. выясняют, какие тела включаются в физическую систему;

5. проверяют, выполняется ли условия В;

6. выбирают инерциальную систему отсчета (относительно которой впоследствии будет определяться значения величины А);

7. находят значение величины А₁ в начале взаимодействия тел;

8. определяют значение величины А₂ в конце взаимодействия;

9. записывают закон сохранения в виде А₁= А₂ или в форме ΔА=0 (А₂–А₁=0);

10. если закон векторный, то обычно проецируют его на оси координат и получают три эквивалентные уравнения , , .

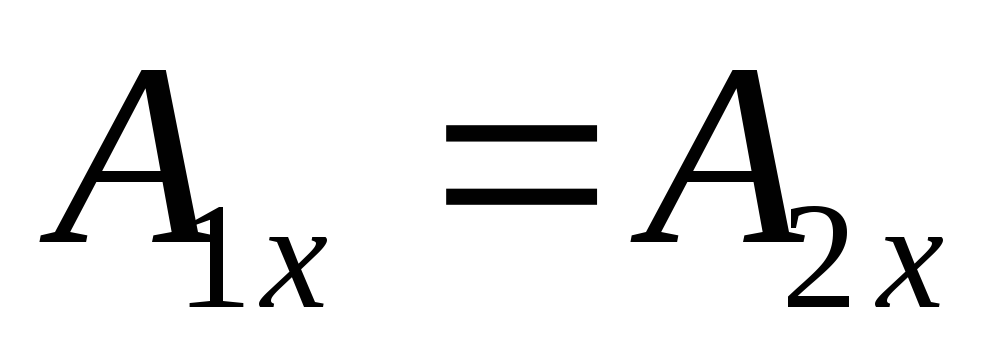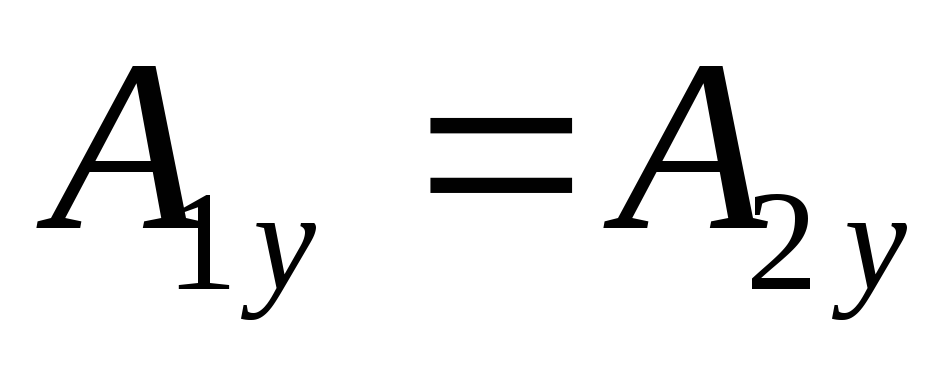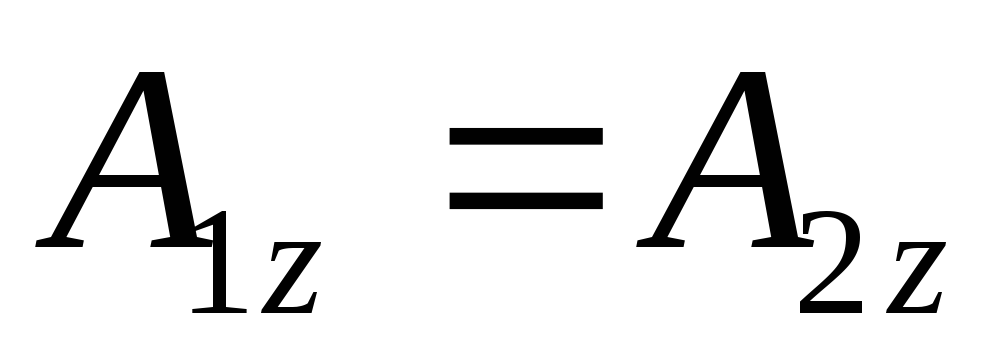Здесь мы рассмотрим только закон сохранения импульса и закон сохранения энергии в механике. Остальные законы обсудим несколько позже.

1. Абсолютно неупругий удар. Два тела массами т₁=2 кг и т₂=3 кг, движутся со скоростям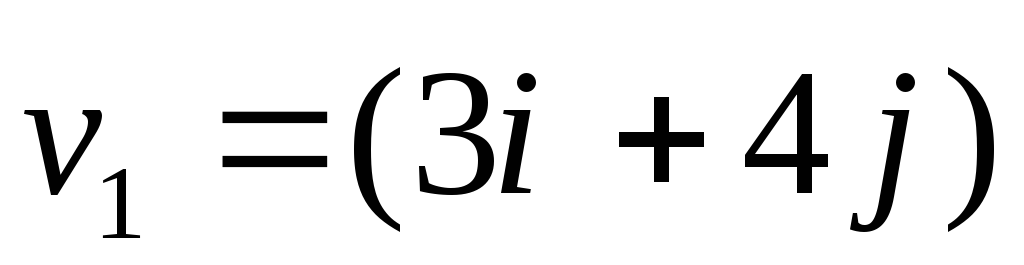и и 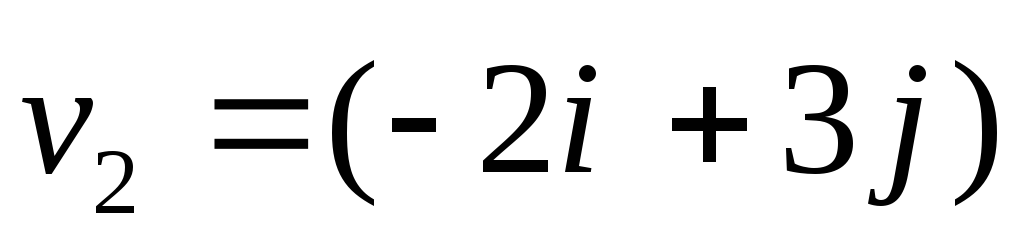относительно некоторой ИСО, сталкиваются абсолютно неупруго. Определить их скорость 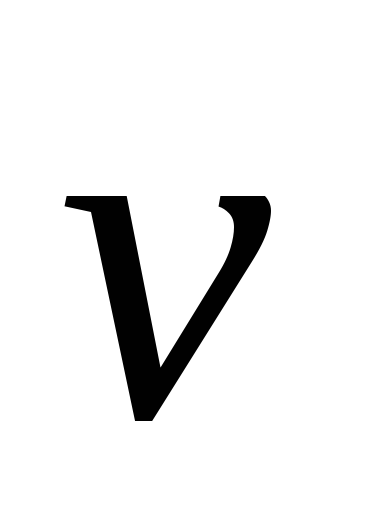после соударения. Действием других тел пренебречь.

Решение. В физическую систему включим два тела: т₁ и т₂. Так по условию влиянием внешних тел можно пренебречь, то выбранная система является замкнутой. Заметим, что законы движения тел (если использовать кинематический подход) найти нельзя, ибо не заданы начальные условия (при t=0 неизвестны координаты тел). Физическое явление заключается в абсолютно неупругом взаимодействии двух тел замкнутой системы. Даны массы и скорости тел до взаимодействия, требуется определить скорости тел после взаимодействия.

Применим закон сохранения импульса. Возможность применения этого закона проверена. ИСО выбрана в условиях данной задачи. Определяем импульс каждого тела до взаимодействия и находим их геометрическую сумму: . Далее находим импульс системы после взаимодействия (в результате абсолютно неупругого удара тела движутся с общей скоростью ): . По закону сохранения импульса получаем , отсюда

.

Проецируя это векторное уравнение на оси координат, находим компоненты искомого вектора скорости:

Таким образом, тела будут двигаться вдоль оси OY со скоростью .

Иногда выбранная физическая система в целом не является замкнутой, и, следовательно, закон сохранения импульса в этом случае применять нельзя. Однако она может быть замкнутой по какому-либо направлению (например, вдоль оси ОХ), т.е. алгебраическая сумма проекций внешних сил на это направление равна нулю. Тогда (только для этого направления) можно записать закон сохранения импульса в скалярной форме .

2. Тележка с песком массой М=100 кг движется прямолинейно и равномерно по горизонтальной плоскости со скоростью v₀=3 м/с (рис. 2.7). Шар массой т=20 кг падает без начальной скорости с высоты h=10 м и попадает в тележку с песком. Определить скорость тел после их взаимодействия. Трение отсутствует.

Р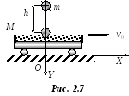ешение. В физическую систему включим тележку с песком (они рассматриваются как одно тело) и шар (рис. 2.7). Выбранная физическая система не замкнута (до взаимодействия на шар действовала сила тяготения Земли, и эта сила не уравновешивалась никакой другой внешней силой). Следовательно, в целом закон сохранения импульса для этой системы применять нельзя. Однако в направлении перемещения тележки на тела действие внешних сил скомпенсировано и, следовательно, для этого направления закон сохранения импульса применять можно. Инерциальную систему отсчета свяжем с Землей, оси координат направим, как показано на рисунке. Составляющая вектора импульса системы в направлении оси ОХ до взаимодействия ; эта же составляющая после взаимодействия , где искомая скорость. По закону сохранения импульса,

,

откуда

. (2.24)

Подстановка числовых значений дает v=2,5 м/с.

Из уравнения (2.24) видно, что искомая скорость не зависит от высоты h и, следовательно, в условиях данной задачи это лишняя физическая величина.

Можно было бы в физическую систему включить и третье тело – Землю. Тогда система из трех тел является замкнутой. Так как Земля считается телом системы и под действием силы тяготения должна двигаться ускоренно (относительно какой-либо ИСО), то, строго говоря, связывать с Землей ИСО нельзя. Но легко показать, что скорость и ускорение Земли (в условиях данной и подобных задач, где массы тел малы по сравнению с массой Земли) в любой момент времени столь малы, что ими можно пренебречь, считая Землю за неподвижное тело.

Найдем, например, скорость Земли в момент взаимодействия с шаром (это максимальная скорость Земли в условиях данной задачи). Очень часто в физике выбирают ИСО, связанную с центром масс системы (СЦМ) или с центром инерции (ЦИ) системы. Центром масс системы называют точку, радиус-вектор которой определяется из уравнения

. (2.25)

Можно показать, что центр масс системы движется как материальная точка, масса которой равна массе системы, а действующая сила равна геометрической сумме всех внешних сил, действующих на систему (теорема о движении центра масс). Запишем уравнение движения центра масс:

,

где масса системы,

вектор скорости центра масс,

геометрическая сумма внешних сил.

Если система замкнута, то и const, т.е. центр масс замкнутой системы движется равномерно и прямолинейно. Следовательно, система отсчета, связанная с центром масс такой системы, является инерциальной. Так как в СЦМ начало координат совпадает с центром масс, то и из (2.25) находим

. (2.26)

Продифференцировав уравнение (2.26) по времени t, получим

, (2.27)

т.е. импульс замкнутой системы относительно СЦМ равен нулю в любой момент времени. Применим этот результат к расчету скорости Земли при ее взаимодействии с шаром (рис. 2.8). На этом рисунке начало координат СЦМ – точка О – смещено в право. Из уравнения (2.27) находим

, (2.28)

где М – масса Земли,

v_З – ее скорость,

т – масса шара,

v_ш – скорость шара.

Из уравнения (2.28) определим скорость Земли:

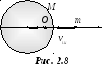
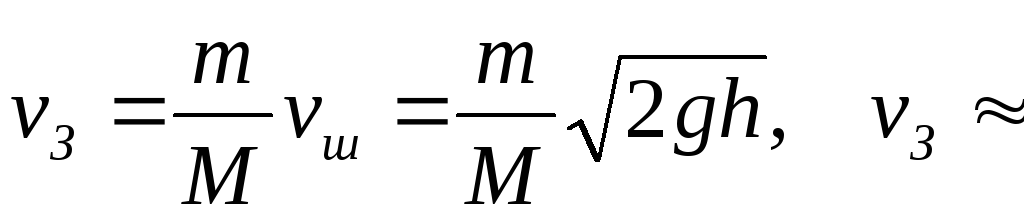5·10^-23 м/с.

полученная скорость фантастически мала. Двигаясь с такой скоростью, Земля переместится на расстояние, равное 1 см, за время лет. В дальнейшем при исследовании движения тел, массы которых малы по сравнению с массой Земли, мы будем пренебрегать воздействием этих тел на Землю, считая ее неподвижной.

Закон сохранения энергии в механике связан с понятиями кинетической Е_к и потенциальной Е_п энергий. Очень важным здесь является также понятие работы А. Как известно, сила на элементарном перемещении совершает элементарную работу

. (2.29)

Работа силы на пути S выражается интегралом

, (2.30)

где интеграл берется вдоль кривой S.

При движении по прямой (например, вдоль оси ОХ)

,

где угол между вектором силы и направлением оси ОХ.

Работа силы на участке от х₁ до х₂ в этом случае определяется формулой

.

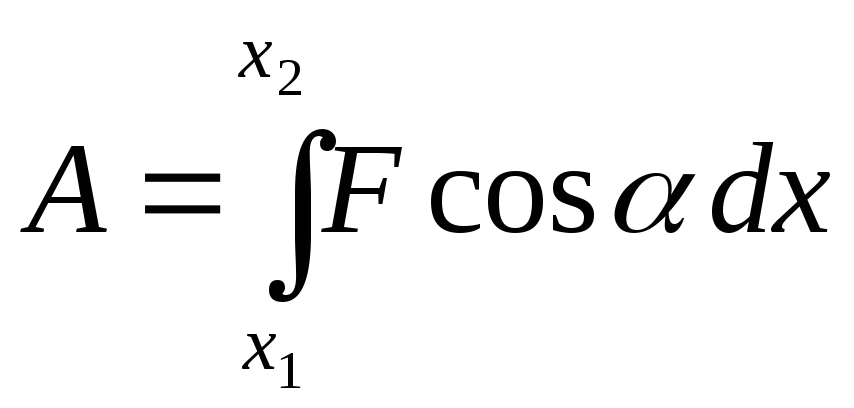Если сила постоянна, то вычисление ее работы не составляет обычно большого труда. При расчете работы переменной силы часто используют метод ДИ (см. 1.2.3). ограничимся прямолинейным случаем и предположим, что . Сила может зависеть от координаты х (в общем случае и от у и z), от компоненты скорости (в общем случае и от других компонент вектора скорости ) и от времени t.

Если сила является функцией только координаты х, то элементарная работа: , а работа на участке от х₁ до х₂

.

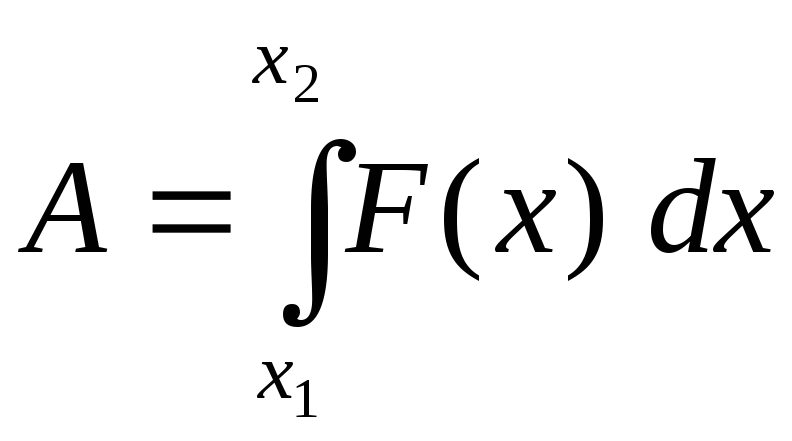2. Небольшое тело А начинает скользить с высоты h по наклонному желобу, переходящему в полуокружность радиуса h/2 (рис. 2.9). Пренебрегая трением, найти расстояние h до наивысшей точки его траектории (момент отрыва от желоба) и скорость v тела в этой точке.

Решение. В физическую систему включим три тела: Землю, желоб и тело А. Физическое явление заключается в скольжении небольшого тела, которое можно принять за материальную точку, по некоторой поверхности. При движении тела по желобу на него будут действовать две силы (сила трения отсутствует по условию задачи): сила нормальной реакции опоры , действующая в любой точке траектории перпендикулярно векторам скорости и перемещения, следовательно, не совершающая работы (не изменяющая механической энергии), и сила тяжести . Так как в выбранной физической системе сила тяжести является внутренней и по своей природе консервативной силой, то в такой системе будет выполняться закон сохранения механической энергии.

П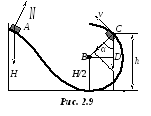редположим, что на высоте h (точка С) от основания желоба произойдет отрыв тела (наивысшая точка траектории). Этот момент соответствует обращению в ноль силы нормальной реакции опоры , т.е. тело уже перестает давить на опору, а опора в свою очередь на тело. Теперь только составляющая силы тяжести в точке отрыва будет придавать телу центростремительное ускорение. Согласно второму закону Ньютона:

, (2.31)

где центростремительное ускорение.

Закон сохранения механической энергии позволяет записать следующее равенство:

, (2.32)

где изменение (уменьшение) потенциальной энергии от момента старта до момента отрыва,

изменение (увеличение) кинетической энергии тела, а так как начальная кинетическая энергия равна нулю, то просто кинетическая энергия в точке отрыва.

Из прямоугольного ΔBCD следует, что

. (2.33)

Решая совместно систему уравнений (2.31) – (2.33) найдем

.