При изучении строения атома эта формула имела решающее значение. Важнейшим выводом из этой формулы, который в то время был сделан, являлся вывод о возможности использования ее для определения числового значения заряда Z атомного ядра: в пределах ошибки измерений заряд ядра совпадает с номером места, занимаемого атомом в периодической системе, т. е. с порядковым номером. Дальнейшие измерения доказали, что закон Кулона выполняется вплоть до очень малых значений p ( 10 Одновременно это число давало представление о размерах атомного ядра.

На рис. 22,б показаны траектории ˛-частиц при двух различных значениях энергии.

6.4Движение электрона в поле атомного ядра, описываемое классической теорией

Очень кратко рассмотрим этот вид движения, так как он в качестве первого приближения к действительности сыграл важную роль на ранней стадии развития квантовой теории. Определим сначала, как зависит полная энергия электрона от формы эллипса. Воспользуемся равенством центробежной и кулоновской сил в самой удобной для обсуждения точке эллипса A, т.е. в точке наибольшего удаления от ядра (рис. 23):

Здесь A и rA могут быть выражены с помощью длины большой полуоси a и эксцентриситета :

Отсюда следует, что полная энергия зависит только от длины большой оси. Учитывая более поздние результаты, имеет смысл привести значения параметров

движения p' D mr v' D mr 2'P, относящихся к точке A:

p' D a.1 C /vAm:

Выражая отсюда vA и подставляя полученное выражение в уравнение (13), находим

35

Задавая энергию и момент количества движения, можно однозначно определить форму орбиты. Из уравнения (13) рассчитывается длина большой оси a; из уравнения

получающегося в результате перемножения равенств (14) и (15), определяется отношение b=a (эксцентриситет).

36

7Основы электронной и ионной оптики. Оптический закон преломления в применении к электрическому и магнитному полям.

7.1Аналоги оптического закона преломления в электрическом и магнитном полях

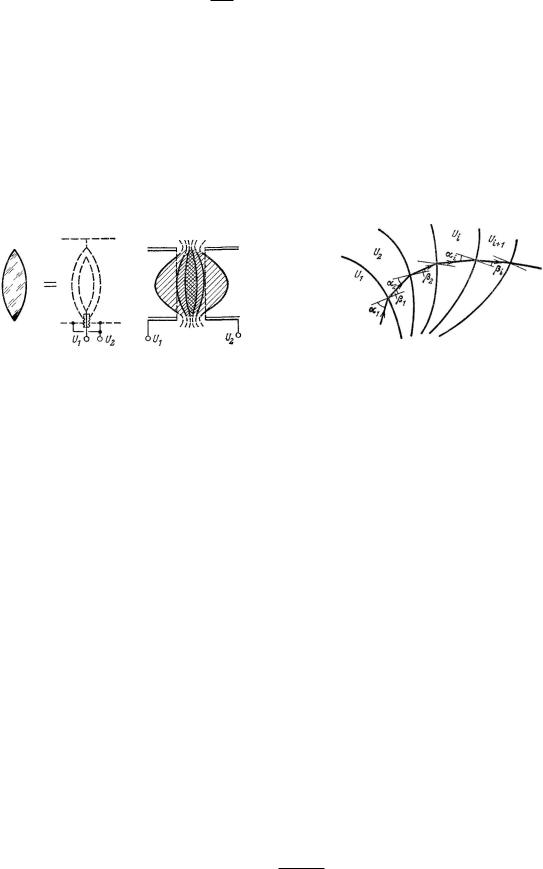
Вболее сложных полях описание движения частиц, естественно, усложняется. В практически важных случаях можно, несмотря на существенные трудности, путем интегрирования уравнения движения получить количественные результаты. Однако можно прийти к достаточно общим количественным представлениям и путем использования аналогии, пригодной для количественных расчетов и имеющей решающее значение как с принципиальной, так и научно-исторической точек зрения. Траектория заряженной частицы, движущейся в произвольном электростатическом поле, совпадает с траекторией луча света, распространяющегося в среде, показатель преломления которой изменяется по заданному закону. Коэффициент преломления в каждой точке пространства определяется локальным значением измеренного напряжения. Обсудим теперь эту аналогию более подробно.

Ход световых лучей описывается геометрической оптикой. Для получения всех закономерностей геометрической оптики в известной степени достаточно утверждения, что свет в однородной и изотропной среде распространяется прямолинейно, а на границе двух сред преломляется согласно закону Декарта—Снеллиуса

Чтобы получить аналогичное явление для электрона, движущегося в электростатическом поле, рассмотрим, какое преломление испытает траектория электрона, если он переходит из области пространства с потенциалом U1 в область пространства с потенциалом U2 (рис. 24).

Рис. 24. Сравнение оптического закона преломления с

электронно-оптическим.

Рис. 25. К выводу закона преломления в электронной оптике.

Так как потенциал внутри каждой отдельной области пространства принимается постоянным, то напряженность поля в этих областях равна нулю. Но между этими двумя частями пространства, т.е. в промежуточном слое, имеется поле, перпендикулярное

37

граничной поверхности. Таким образом, при прохождении частицы тангенциально направлению этого поля она не ускоряется:

v1t D v2t :

Но, как показано на рис. 25,

v1t D v1 sin ˛1 D v2t D v2 sin ˛2;

поэтому

v1 sin ˛1 D v2 sin ˛2

Если подставить сюда значение скорости, полученное из уравнения 12 mv2 CqU D W0,

Если W0 D 0, т.е. частица начинает двигаться без начальной скорости из точки с потенциалом, равным нулю, то формула будет иметь вид

Сравнение уравнения (17) с законом преломления света Декарта-Снеллиуса показывает, что роль оптического показателя преломления n играет выражение

r

ne D pW0 C eU D m2e v;

которое может рассматриваться как электрический коэффициент преломления. Следует p

подчеркнуть, что неважно приведен ли в формулу или опущен множитель me =2. В последующем мы с тем же успехом будем использовать выражение

ne D v или ne D me v:

Исследуем также, что будет происходить при пересечении электроном или электронным лучом тонкого однородного магнитного поля, перпендикулярного к плоскости пучка Луч и в этом случае отклоняется, соотношения оказываются более сложными, показатель преломления зависит и от угла падения, так что эквивалентная среда в случае магнитного поля не только неоднородна, но и анизотропна. Следует упомянуть, что в общем случае показатель преломления записывается в форме

38

Если имеет место и электростатическое поле, то, выражая скорость так, как это было показано раньше, можно для показателя преломления в общем случае написать-

s

Обсуждение метода рассмотрения, основанного на аналогии, проводится с целью сделать наши представления о реальном процессе более наглядными и по возможности получить соответствующие рекомендации для эксперимента. Законы геометрической оптики наглядны и хорошо известны, так что мы будем к ним часто возвращаться при обсуждении движения зарядов в электрическом поле. Аналогия при движении электрона в магнитном поле ищется в кристаллооптике, законы которой значительно сложнее. В данном случае значительно проще рассматривать механическое движение электронов, чем его оптический аналог.

Приближенная траектория — ломаная линия, образованная прямолинейными отрезками, построенными по закону преломления.

В действительности обычно встречаются скалярные и векторные потенциалы, изменение которых происходит непрерывно, а не скачкообразно. В соответствии с этим и траектория электронного пучка представляет собой не ломаную, а непрерывно искривляющуюся линию. Чтобы осуществить приближенный количественный расчет и выявить сходство с оптическими приборами, можно поля с непрерывным распределением потенциала разделить на тонкие слои со скачкообразно изменяющимися потенциалами (рис. 26).

Указанная аналогия имеет огромное практическое значение, так как она позволяет перенести хорошо разработанную теорию, а также наглядные методы расчета оптики и оптических приборов на описание движения электронов и электронной аппаратуры. Аналогия сразу приводит к мысли о существовании электронных линз, т.е. к представлению о фокусирующих устройствах. Приведенные выше представления можно использовать для приближенного определения траектории частицы в любом сложном электростатическом поле при известных эквипотенциальных поверхностях. В самом грубом приближении значение потенциала можно рассматривать постоянным вдоль каждого отрезка (рис. 27); следовательно можно приближенно представить траекторию электрона на основании закона преломления ломаной линией; при этом можно определить по порядку отдельные углы, используя для этого соотношение

39

Лучшее приближение — естественно, с большей затратой труда — достигается, если рассматривать электрическое поле между двумя эквипотенциальными поверхностями постоянным, т.е. потенциал — линейным. В этом случае орбита составляется из отрезков параболы. Однако это уже выходит за рамки метода аналогий.

7.2Общие оптико-механические аналогии

Эти аналогии, естественно, имеют более глубокое обоснование. Законы механики, так же как и оптики, могут быть выведены из вариационного принципа Ферма или Мопертюи.

К принципу Ферма можно подойти следующим путем. Пусть задана среда с любым непрерывно или скачкообразно изменяющимся в пространстве показателем преломления. Свет исходит из точки среды P1 и после прохождения какого-то пути попадает в точку Р2 (рис. 28). Разделим траекторию на элементы ds и для каждого элемента траектории построим произведение nds, т.е. умножим каждый элемент траектории на значение измеряемого около него показателя преломления. Полученные величины суммируются, т.е. мы получаем линейный интеграл:

ZP2

P1

Рис. 28. Иллюстрация к истолкованию принципа Ферма.

Естественно, что точки P1 и P2 можно соединить семейством любых других кривых, не совпадающих с действительным ходом луча. Для каждой кривой можно также написать подобный интеграл. Если рассчитать этот интеграл для всех возможных кривых, то согласно принципу Ферма для истинного пути луча получается либо наибольшее, либо наименьшее, т.е. экстремальное, значение. Поэтому для нахождения действительного пути следует искать кривую, для которой выполняется условие

ZP2

P1

Это задача вариационного исчисления. В задачах такого типа ищут неизвестную функцию (в данном случае уравнение пути луча), для которой ранее определенный интеграл принимает экстремальное значение.

Оптическому принципу Ферма можно дать очень простое физическое толкование. Известно, что скорость света в среде v связана с показателем преломления этой среды формулой v D c=n. Следовательно, вместо показателя преломления можно подставить

40

c=v. Тогда принцип Ферма запишется в виде

Так как c является постоянной, то справедливо равенство

Величина ds=v выражает время прохождения светом элемента пути ds. Поэтому интеграл выражает время, в течение которого свет идет от точки P1 до точки P2. Таким образом, возможна другая формулировка принципа Ферма: свет попадает из одной точки в другую за минимальное время (иногда бывает, что время прохождения максимально, но значение интеграла остается экстремальным).

С другой стороны, механические соотношения можно получить из принципа Мопертюи. Пусть частица движется от точки P1 к точке P2 в любом потенциальном поле по однозначно определенной траектории и пусть скорость в каждой точке определена. Согласно принципу Мопертюи траектория определяется на основании требования

Из всех возможных траекторий частица выбирает такую, для которой интеграл (22) принимает экстремальное значение. Если выразить v через полную и потенциальную

В рамках классической физики m является величиной постоянной, так что умножение на m, так же как и на любую другую постоянную, не влияет на определение экстремального значения.

Следует упомянуть, что в случае магнитного поля истинная траектория может быть определена на основании требования

С принципиальной точки зрения, более важной является связь рассмотренных выше положений с волновой механикой, дающей правильное микрофизическое описание движения частиц.

41

Для полноты описания остановимся на рассмотрении вопроса о том, как связан принцип Мопертюи с самым общим вариационным принципом — принципом Гамильтона и как последний связан через основные уравнения вариационного исчисления с уравнениями Лагранжа второго рода, непосредственно приводящими к уравнениям движения Ньютона.

Вариационный принцип Гамильтона заключается в следующем. Пусть в любой системе, характеризующейся обобщенными координатами q1.t /; q2.t /; : : : qf .t /, кинетическая энергия системы Wк.qP1; : : : ; qPf / является функцией обобщенных скоростей, образованных путем дифференцирования по времени обобщенных координат q1; : : : ; qf , а потенциальная энергия Wп.q1; ; : : : ; qf / — функцией координат точки. Для любого интервала времени от t1 до t2 движение согласно принципу Гамильтона происходит так, что выражение

принимает экстремальное значение. Это обычно выражается приравниванием нулю вариации интеграла

В случае одной частицы это выражение примет вид:

Эта формула выражает принцип Мопертюи.

Задача вариационного исчисления как математической дисциплины в самом простейшем случае заключается в отыскании функции y D y.x/, при которой значение

интеграла

Zx2

F.x; y; y0/dx

x1

42

становится экстремальным, т.е. максимальным или минимальным. Функция F.x; y; y0/ задается. Для решения задачи составляют так называемое Эйлерово дифференциальное уравнение:

Решением этого уравнения является искомая функция y.x/. Таким образом, основная задача вариационного исчисления сводится к решению приведенного дифференциального уравнения.

Если F является функцией многих переменных yi .x/, которые все зависят от одной переменной x, то дифференциальное уравнение, идентичное предыдущему, записывается для каждой переменной yi . В результате получается система дифференциальных уравнений, решения которой дают искомые функции yi .x/.

Для определения неизвестных функций, входящих в выражение принципа Гамильтона, можно записать уравнения вариационного исчисления Эйлера:

Эти уравнения называют уравнениями механики Лагранжа 2-го рода. Здесь обобщенные координаты точки qi представляют собой зависимые переменные yi , а t играет роль независимой переменной x.

Связь этих уравнений с уравнением движения Ньютона сразу становится понятной, если рассматривать движение отдельной материальной точки. Тогда справедливы равенства

т.е. к хорошо известному закону «произведение массы на ускорение равно силе». Если

Уравнение (29) может быть переписано таким образом, что получается соотношение (24).

43

Вариационный принцип применим и для нахождения уравнения орбиты в самом общем случае. А именно, если написать уравнение Эйлера для вариационного принципа:

(здесь и ниже применяется упрощенное обозначение eU D W0 CeU ). Теперь уравнения Эйлера имеют вид

Подставляя сюда значение n, получаем уравнения:

Решения этих уравнений x D x.z/, y D y.z/ дают траектории электрона. Далее рассматривается решение такого уравнения для частного случая, не обращаясь при этом более к обобщенным вариационным принципам.

44

7.3Определение фокусного расстояния на основании оптической аналогии

Оптические собирающие линзы или системы являются в общем вращательно-сим- метричными. Соответственно этому можно ожидать, что и электронные пучки могут быть сфокусированы при помощи электрического и магнитного полей, являющихся вращательно-симметричными. Приближенно вращательно-симметричное электрическое поле создается с помощью системы линз, показатель преломления которой скачкообразно изменяется, как это показано на рисунке 26. Для электронного луча существует связь показателя преломления любого слоя с потенциалом, имеющая вид:

p

n D W0 C eU :

Сначала определим, пользуясь законами оптики, фокусное расстояние разграниченных сферическими поверхностями частей пространства с показателями преломления n1 и n2 для параксиального случая, т.е. для случая, когда лучи идут в пределах малого телесного угла около оси (рис. 29).

а)

б)

Рис. 29. Схема, поясняющая вывод формулы фокусного расстояния электронной линзы. Значение r на обоих рисунках одно и то же.

Согласно закону преломления

При малых углах справедливо выражение

˛1 D n2 ˛2 n1

или

˛1n1 D ˛2n2:

45

Для лучей, близких к оси, можно на основании геометрических соображений напи-

Чтобы проследить за дальнейшим ходом луча через следующую поверхность с иной кривизной и затем в третьей среде с новым показателем преломления, следует рассчитать фокусное расстояние, что можно сделать на основе подобных же рассуждений, но только учитывая, что во второй среде луч идет уже не параллельно оси, а под некоторым углом ˛1 ˛2 к ней (рис. 29). Если угол наклона перпендикуляра, проведенного к точке падения

Если обозначить разность показателей преломления через d n, а индекс 3, относящийся к пространству, расположенному справа, заменить индексом b (см. рис. 29), то

Подобным же способом можно показать, что это соотношение справедливо для любого числа слоев. При слоях очень тонких, т.е. в полях изменяющихся квазинепрерывно,

46

интегрирование можно распространить на любую область пространства, где n изменяется.

Используя далее оптическую аналогию p

Радиус кривизны осесимметричных полей согласно теории электростатических по-

Величина fb представляет собой расстояние, на котором электрон, попавший на линзу слева параллельно оси, пересекает эту ось.

Аналогично получают фокусное расстояние для электрона, приходящего справа:

где a — индекс объекта.

Если в точке, где скорость электрона равна нулю, значение потенциала полагается тоже равным нулю, то и энергия частицы в этой точке будет равна нулю. Тогда сумма W0 кинетической и потенциальной энергий все время будет оставаться равной нулю. Такой выбор координат позволяет исключить U0 из формул (35) и (36)

Проведенные анализы справедливы лишь для тонких и слабых линз, у которых фокусное расстояние велико по сравнению с размерами части пространства, в которой изменение показателя преломления отлично от нуля, а также лишь для случая, когда расстояние электрона от оси внутри линзы почти не меняется, так что частица изменяет лишь направление движения.

47