
- •Движение частиц в одновременно действующих электрическом и магнитном полях
- •Движение частиц в одновременно действующих электрическом и магнитном полях значительной протяжённости
- •Возрастание массы при увеличении скорости
- •Эквивалентность массы и энергии
- •Общие следствия из уравнения движения
- •Форма траектории
- •Движение электрона в поле атомного ядра, описываемое классической теорией
- •Аналоги оптического закона преломления в электрическом и магнитном полях
- •Расчет фокусного расстояния тонкой линзы на основании уравнения движения
- •Электростатическое поле как спектрометр
- •Магнитное поле как спектрометр
- •Каскадный генератор
- •Синхротрон и синхрофазотрон
- •Микротрон
- •Максимальная энергия, достижимая с помощью ускорителей
- •Характеристика диода в высокочастотном поле
- •Фазовая фокусировка
- •Излучающий электрон с точки зрения классической электродинамики
- •Излучение Черенкова
- •Постулаты Бора
- •Спектр излучения
- •Простейшая форма принципа соответствия
- •Модель атома Бора-Зоммерфельда
- •Недостатки теории Бора
- •Аналог волновой оптики
- •Правила вычисления вектора состояния
- •Математические основы квантовой механики
- •Временное изменение ожидаемого значения
- •Роль коммутативности операторов
- •Наиболее важные операторы
- •Система с одним электроном
- •Поведение одноэлектронной системы в магнитном поле
- •Влияние магнитного момента ядра на энергетические состояния атома
- •Понятие микросостояния в квантовой механике
- •Определение распределения, соответствующего состоянию равновесия
- •Связь с макроскопической термодинамикой
- •Классический газ
- •Электронный газ
- •Фотонный газ
- •Природа химической связи
- •Строение твердого тела
- •Распределение потенциальной энергии в металле
- •Зонная теория твердого тела
- •Электроны в периодическом потенциальном поле. Одномерный случай

Эта величина, согласно статистике Фермн—Дирака (см. уравнение (418)), составляет:
|
cvFD D |
n 2 k2T |
|
; |
(420) |
||||||||||
|
|
|
2 WF0 |
||||||||||||
а согласно статистике Максвелла—Больцмана (см. уравнение (419)) |
|
||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||
|
|
cvMB D |
|
|
nk: |
|
|
|
(421) |
||||||
2 |
|
|
|
||||||||||||
Отношение обеих величин равно: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
cvFD |
|
2 kT |
|
|
|
|
|||||||
|
|
|
|
D |
|
|
|
|
|
: |
|
|
|||
cvMB |
|
3 WF0 |
|
|
|
||||||||||
Значение WF0 равно 10 эВ 10 18 Дж. Отсюда, например, для T D 1000 К получаем: |
|
||||||||||||||
|
cvFD |
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
4:5 10 |
|
|
: |
|
||||||||
cvMB |
|
|
|
||||||||||||
Таким образом, величина удельной теплоемкости электронного газа по статистике Ферми— Дирака много меньше, чем удельная теплоемкость, определенная исходя из классической статистики.
Теперь понятно, почему в выражение удельной теплоемкости металлов не входит число степеней свободы электронов.
25.3 Фотонный газ
Теперь применим статистику Бозе для определения распределения по энергиям излучения, заключенного в абсолютно черном теле объемом V .
Если внутри этой полости существует термодинамическое равновесие, то распределение фотонов по различным энергетическим состояниям может быть определено по формуле (333) п. 24.3. Так как число фотонов может изменяться (стенка может их как поглощать, так и испускать), отпадает условие dN D 0, что учитывается выбором ˛ D 0. Если использовать выражения W D h и ˇ D 1= kT и обозначить число квантовых состояний в диапазоне от до C d через dz, то число фотонов, энергия которых
находится в диапазоне h и h. C d/, составит: |
|
||||||
|
|
|
dz |
|
|||
dN |
|
|
|
|
|
: |
(422) |
D e |
h |
1 |
|||||
|
kT |
|
|
|
|||
Как известно, для импульса фотона справедливо соотношение |
|
||||||
|
p D |
h |
: |
|
|
||
|
|
|
|
||||
|
c |
|
|
||||
Из уравнения (307) § 24 найдем число квантовых состояний в диапазоне изменения
импульса от p до p C dp:
dz D 4 V 2 d: c3
Если при этом учесть, что в каждом квантовом состоянии могут находиться два фотона, то число фотонов, приходящихся на энергетическую зону в интервале h и h. C d/, составляет:
dN |
D |
8 V 2 |
|
|
|
1 |
d: |
(423) |
|
c3 |
|
|
h |
|
|
||||
|
|
e |
|
1 |
|
||||
|
|
kT |
|
|
|||||
202

Если умножить dN на энергию h единичного фотона, то получим энергию излучения в диапазоне от до C d . Если разделить эту величину на объем тела, то получим объемную плотность энергии, приходящуюся на указанный интервал частот:
. /d |
D |
8 h 3 |
|
|
|
1 |
d: |
(424) |
|
c3 |
|
e |
h |
|
1 |
||||
|
|
|
|
|
|||||
|
|
kT |
|
|
|
||||
Это формула излучения Планка.
Энергию, излучаемую поверхностью в единицу времени, достаточно просто определить, вырезав в стенке абсолютно черного тела отверстие с достаточно малой поверхностью, чтобы не нарушить термодинамическое равновесие внутри абсолютно черного тела.
Из теории электромагнитных волн мы знаем, что произведение объемной плотности энергии на скорость света равно мощности излучения электромагнитных волн. Вследствие изотропности пространства прибавляется еще множитель 1=4 . Отсюда
I d |
D |
c |
D |
2h 3 |
|
|
|
1 |
d: |
|
||
|
. /d |
|
|
|
|
|
|
(425) |
||||
4 |
c2 |
|
e |
h |
|
1 |
||||||
|
|
|
kT |
|
|
|
||||||
Здесь I обозначает мощность, приходящуюся на интервал частот от до C d , падающую на единицу поверхности нормально к ней и излучаемую внутри единичного телесного угла. Если частоту выразить через длину волны, то получим:
I d |
D |
2hc2 |
|
1 |
|
d : |
||
5 |
e |
hc |
1 |
|||||
|
kT |
|
|
|||||
На рис. 109 представлен график зависимости излучаемой мощности от длины волны для разных температур T .
Рис. 109. Спектральная плотность энергии, излучаемой единицей поверхности черного тела в телесный угол 2 .
Формула излучения Планка важна при решении очень многих практических проблем, в частности при рассмотрении вопросов, связанных с лучистой теплопередачей и светотехникой. Ее теоретическое и историко-научное значение особенно велико, так как квантовая гипотеза Планка возникла при выводе именно этого закона.
203

К закону Стефана—Больцмана можно прийти следующим образом: из уравнения (425) получаем мощность излучения в телесном угле 2 в интервале частот от до C d :
". ; T /d |
D |
2 h 3 |
|
|
|
1 |
d : |
|
c2 |
e |
h |
|
1 |
||||
|
|
|
||||||
|
kT |
|
|
|||||
Тот факт, что это уравнение не может быть получено из уравнения (425) простым умножением на 2 , объясняется тем, что в направлении, которое составляет с нормалью к единичной поверхности угол # , следует учитывать лишь площадь 1 cos # . Соответственно получим:
|
|
|
|
|
|
|
|
|
2 =2 |
|
|
|
|
|
|
|
|
|
". ; T /d |
|
2h 3 |
|
|
|
1 |
d |
Z0 |
cos # sin # d# d' |
|
2 h 3 |
|
|
|
1 |
d : |
||
|
|
|
|
h |
|
|
|
|
|
|
h |
|
|
|||||
|
D |
c2 |
e |
|
1 |
|
Z0 |
D |
c2 |
|
e |
|
1 |
|
||||
|
kT |
|
|
|
kT |
|
|
|||||||||||
Общая мощность излучения в диапазоне частот 0 1 составит, следовательно,
|
|
|
|
|
|
|
|
|
|
|
2 h |
1 |
|
3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Pизл |
|
|
|
|
|
|
|
|
Z0 |
|
|
|
|
d : |
|
|
|
||
|
|
|
|
|
|
D c2 |
|
|
|
h |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
e |
kT |
|
1 |
|
|
|
|
|||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
D |
e |
h 1 |
|
|
|
|
|
D |
|
|
|
h |
C |
e |
2h |
C |
: : : |
C |
e |
|||||||
|
e kT 1 |
|
|
1 e kT |
|
|
|
|
|
|
|
|
|||||||||||||||
|
kT |
|
e kT |
kT |
|||||||||||||||||||||||
|
|
h |
|
|
|
|
h |
|
|
|
|
|
|||||||||||||||
и |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
kT |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
3e |
nh |
d |
|
|
3! |
|
; |
|
|
|
||||||||
|
|
|
|
|
|
0 |
kT |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nh |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nh
kT C : : :
получаем: |
1 C |
|
|
|
|
C : : : : |
|||
|
h k4T 43! |
1 |
|
1 |
|||||
Pизл D |
2 |
|
|
|
C |
|
|
||
c2 |
h4 |
24 |
34 |
||||||
Так как сумма членов бесконечного ряда имеет конечное значение 4=90, получим в результате:
|
2k4 |
Pизл D |
60~3c2 T 4 D T 4: |
Величину называют константой Стефана—Больцмана. Она равна:
|
2k4 |
2 5k4 |
||
D |
|
D |
|
D 5:67 10 8 Вт м2 К 4: |
60~3c2 |
15h3c2 |
|||
204
26 Строение твердого тела. Зонная теория твердого тела.
26.1 Природа химической связи
Выше был рассмотрен особый случай химической связи — молекула водорода. Только квантовая механика могла разъяснить эту гомеополярную или ковалентную связь. С классической точки зрения казалось, что может быть оправдана только гетерополярная, электровалентная или ионная связь, в дальнейшем прежде всего будет рассмотрен последний тип связи, а в заключение мы снова обратимся к гомеополярной связи.
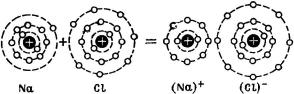
Известно, что атомы элементов находятся в свободном состоянии в редчайшем случае. Обычно в газообразном состоянии они объединяются в молекулы. Одноатомными являются прежде всего инертные газы. Это объясняется тем, что атомы этих элементов имеют замкнутую электронную оболочку. Эта конфигурация отличается очень высокой стабильностью. Поэтому неудивительно, что если возникает возможность, то и другие элементы обнаруживают сильную тенденцию к образованию конфигурации, подобной инертному газу. В качестве примера рассмотрим NaCl (рис. 110). Натрий имеет 11 электронов, из которых 2 — на наиболее близко расположенной, 8 — на следующей оболочке (эти две оболочки вместе аналогичны электронной конфигурации в неоне) и еще один электрон — на наружной оболочке. Из 17 электронов хлора 10 внутренних обладают конфигурацией инертного газа, о которой говорилось выше, а к 7 электронам наружной оболочки достаточно прибавить еще один электрон, чтобы получить конфигурацию, соответствующую следующему инертному газу — аргону. Следовательно, если атом Na отдает свой электрон атому Cl, то каждый из возникающих таким образом ионов NaC и Сl обладает энергетически выгодной конфигурацией инертного газа. Связь внутри молекулы NaCl объясняется электростатическими силами притяжения между возникающими таким образом ионами. Естественно, что образующаяся при этом молекула каменной соли представляет собой электрический диполь. Поле этого диполя обусловливает возникновение ионного кристалла.
Рис. 110. Пример гетерополярного типа связи: каменная соль.
Аналогично этому возникает и ионная связь в многоатомной молекуле. В молекуле H2SO4, например, атом серы отдает 6, а оба атома водорода — по 1 электрону, так что каждый из четырех атомов кислорода и атом серы приобретают электронную конфигурацию инертного газа. На рис. 111 показана ионная связь серной кислоты и раствора едкого натра.
Валентность элемента при ионной связи определяется числом электронов, которые данный элемент может отдать или принять, чтобы приобрести электронную конфигурацию инертного газа.
Ковалентную связь объяснить с классических позиций невозможно. В случае с молекулой водорода мы видели, что связь осуществляется двумя электронами с противоположно направленными спинами: каждый из этих двух электронов входит в состав каждого из двух атомов, которые, можно сказать, обмениваются между собой этими
205
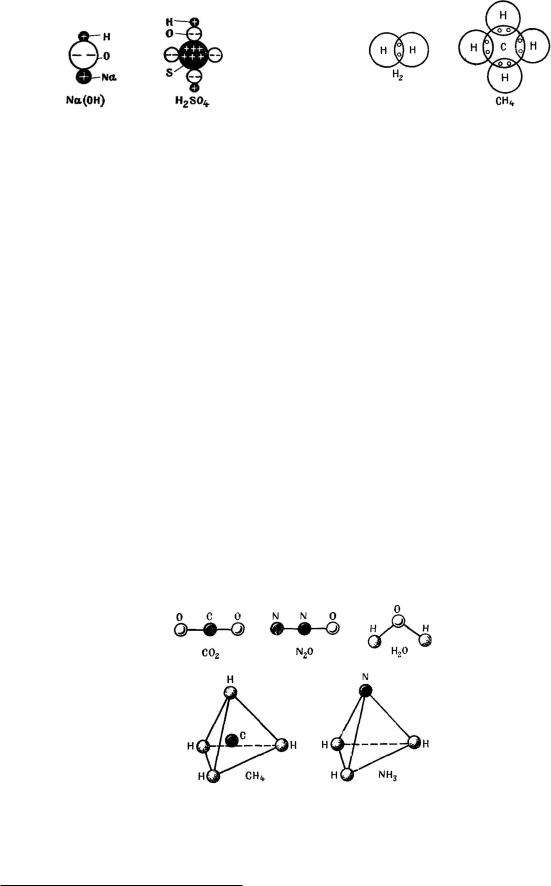
Рис. 111. Многоатомные молекулы с ионной |
Рис. 112. При ковалентной связи электроны, |
связью. |
осуществляющие связь, принадлежат одновре- |
|
менно обоим атомам. |
электронами. Этот результат можно обобщить: электрон любого атома, в котором нет электронов со спином, ориентированным в противоположном направлении, может обеспечить ковалентную связь с другим атомом19. Два электрона двух различных атомов, соединенных таким образом, принадлежат обоим атомам и таким способом обеспечивают связь между ними. С другой стороны, результирующий спин атома обусловлен неспаренными электронами. Удвоенное значение этого результирующего спинового квантового числа S определяет, таким образом, число непарных электронов и одновременно валентность атома. Так как мультиплетность тоже определяется полученным спиновым квантовым числом (M D 2S C 1), то отсюда следует, что валентность равна этой величине мультиплетности минус единица. Однако опытным путем не удалось получить доказательства справедливости этого вывода во всех случаях. Это свидетельствует о том, что валентность не является свойством отдельного атома, независимым от побочных условий, а связана с влиянием других атомов, участвующих в молекулярной связи. Наличие последнего обстоятельства может изменить число неспаренных электронов, например, вследствие того, что один электрон занимает более высокий энергетический уровень, чем определенный в соответствии с принципом Паули в изолированном атоме.
Как показано на рис. 112, стремление к образованию заполненной оболочки обнаруживается и при гомеополярной связи, однако в отличие от ионной связи отдельные электроны принадлежат здесь обоим атомам и благодаря этому обеспечивают заполнение их электронных оболочек, приводящее к электронной конфигурации инертного газа.
Рис. 113. Пространственная конфигурация некоторых многоатомных молекул.
Подводя итоги, можно установить, что при ионной связи неспаренный электрон одного атома объединяется с неспаренным электроном другого атома, причем оба эти
19Правильнее было бы сказать, что ковалентная связь может быть обеспечена между любой парой атомов, содержащих электроны с противоположно направленными спинами, находящиеся на одной молекулярной орбите.
206
