соотношении =. 2r0/, где обозначает длину свободного пробега. Если две молекулы сталкиваются под углом к линии, соединяющей их центры, то «перепрыгиваемое» расстояние будет меньше и сократится до нуля при скользящем соударении. Среднее сокращение пути составляет среднеарифметически как раз r0, так что число соударений, а вместе с этим давление уменьшится на величину, учитываемую множителем

r0

:

Если ввести в это уравнение выражение длины свободного пробега, то согласно уравнению (392) получим:

b D 3p2N 43 r03;

где N означает общее число молекул в объеме V . Окончательная формула уравнения состояния запишется в виде

p.V b/ D RT:

Мы уже видели, что значение константы b приблизительно равно четырехкратному суммарному объему молекул.

Взаимное притяжение молекул до сих пор во внимание не принималось. Но тот факт, что жидкое агрегатное состояние вещества может быть достигнуто при конечных значениях давления, свидетельствует о том, что при достаточно малых расстояниях между молекулами существует большая сила притяжения. При ударе о стенку сосуда молекул газа эта сила притяжения направлена внутрь сосудов, вследствие чего давление газа в противоположном направлении, т. е. наружу, уменьшается. Поэтому, чтобы соотношение (393) сохраняло силу, к давлению, измеренному на стенках сосудов, следует прибавить также давление от взаимного притяжения молекул Реальное уменьшение давления, обусловленное притяжением молекул, с одной стороны, пропорционально числу притягивающихся молекул, с другой — притянутых, так что в конечном счете оно пропорционально квадрату плотности. Если же представить плотность как отношение числа всех молекул к занимаемому ими объему, то величина, о которой идет речь, обратно пропорциональна квадрату объема. Тогда уравнение состояния реального газа с учетом конечного объема

Таким образом, мы получаем уравнение состояния Ван-дер-Ваальса, уже известное из термодинамики. С точки зрения молекулярно-кинетических представлений, значение этой взаимосвязи состоит в том, что входящая в уравнение константа b, которая может быть определена путем макроскопического измерения, непосредственно зависит от числа и диаметра молекул. Отсюда можно определить величину произведения n.2r0/2 и вычислить, исходя из одной характеристики, другую.

25.2 Электронный газ

Функция распределения электронного газа на основе статистики Ферми—Дирака. Мы уже видели, что наиболее вероятное распределение частиц статистика Ферми—Ди-

195

Применим эту статистику к газу, подчиняющемуся статистике Ферми и заключенному в сосуд объемом V , а также к электронному газу.

Уже указывалось, что объем элементарной ячейки в пространстве скоростей равен h3=.m3V /, так что в объеме dvx dvy dvz вокруг точки vx ; vy ; vz насчитывается в общем

ячеек. Так как в каждой ячейке могут располагаться максимум два электрона с противоположной ориентацией спинов, то получают следующее распределение в пространстве

При этом вместо ˛ введена новая величина — энергетический уровень Ферми, определя-

Наши представления о функции распределения станут полными только после определения и объяснения смысла этой величины.

К функции распределения абсолютной величины скорости приходят тем же путем, что и в случае классического газа. Прежде всего мы устанавливаем число частиц, находящихся в сферической оболочке, ограниченной радиусами v и v C dv:

Если применить соотношение для частиц, движущихся в пространстве, свободном

Объединив отдельные функции распределения, получим (см. рис. 108):

196

где WF — параметр с размерностью энергии, величина которого определяется интегралом от функции распределения, взятым по всей области изменения энергии частиц. К рассмотрению величины и роли этого параметра мы вернемся позже. Как видно, в каждой формуле встречается множитель, характерный для статистики:

Рассмотрим теперь поведение этого множителя для случая T D 0, т.е. при абсолютном нуле. Обозначим в данном случае WF .T / через WF0 . Тогда показатель степени

выражения

W WF e kT

стремится к бесконечности, а именно:

Сама экспонента, таким образом, стремится в первом случае к нулю, во втором — к бесконечности. Следовательно, при T D 0

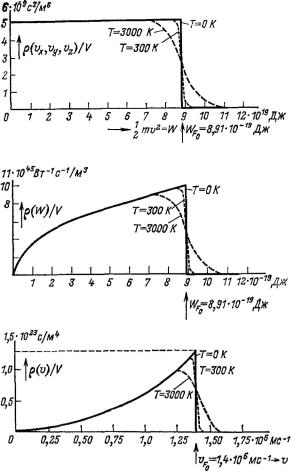
Таким образом, теперь мы имеем три функции распределения для T D 0 (рис. 108, а,б,в). Из распределения компонент скоростей ясно, что если пространство скоростей ха-

рактеризуется значениями ниже или выше значения скорости r

2

vF0 D m WF0 ;

то плотность электронов в пространстве скоростей соответственно постоянна или равна нулю. При T D 0, таким образом, электроны равномерно заполняют в пространстве скоростей сферу радиусом vF0 . В отличие от классической теории электроны, таким

197

образом, даже при абсолютном нуле обладают некоторой определенной энергией. Эта «нулевая энергия» обусловлена принципом Паули, согласно которому не допускается, чтобы все электроны оказались собранными в одной точке в начале координат пространства скоростей, как этого требовала бы в этом случае классическая теория. Максимальная энергия нулевой точки WF0 получила, таким образом, наглядное объяснение. Рассчитаем теперь величину этой энергии.

Общее число электронов составляет:

Эта зависимость может быть получена также путем следующего весьма наглядного рассуждения. При абсолютном нуле электроны, насколько это допускается принципом Паули, стремятся по возможности приблизиться к центру пространства скоростей. Таким образом, они равномерно заполняют некоторую сферу. Число ячеек, располагающихся в этой сфере (т.е. объем сферы, разделенный на объем единичной ячейки), равно половине общего числа частиц, так как в каждой ячейке могут быть размещены две частицы:

Путем соответствующих преобразований приходят к уравнению (404). Можно показать, что WF при E ¤ 0 может быть представлена в виде ряда, первый член которого

Если проверить порядок величин входящих в это уравнение параметров, то даже при температуре T D 3000 4000 К

198

с достаточно хорошим приближением.

Поведение электронного газа при очень высокой температуре. Теперь рассмотрим, как ведет себя электронный газ при очень высоких температурах. Если T 50000 К, то WF , которое в отличие от WF0 не может быть просто физически истолковано, как это следует ожидать исходя из соотношения (406), будет выражаться большим отрицательным числом. Проанализируем теперь уравнение (398):

WF

Исходя из вышеизложенного, e kT 1, так что единицей в знаменателе можно пренебречь, даже при W0 D 0. Таким образом, с хорошим, приближением получим:

ZZC1 ZC1 ZC1

можно легко вычислить путем перехода к полярным координатам, получив в результате

Подстановка численных значений констант подтверждает правильность сделанного ранее предположения:

WF

e kT 1:

Если объединить уравнения (412) и (409), то получим:

которое представляет собой не что иное, как функцию распределения компонент скоростей Максвелла—Больцмана. Таким образом, видно, что распределения Ферми—Дирака

199

при очень высоких температурах переходят в распределение Максвелла—Больцмана. Впрочем, это ясно и из графиков функций распределения Ферми—Дирака, относящихся к высоким температурам (рис. 108). Условием перехода было, как видим,

Как видно из данного уравнения, это условие выполняется не только при очень высоких значениях T , но и при малой плотности частиц N=V или при большой массе частиц m.

Из рис. 108 видно, что при повышении температуры концентрация электронов, обладающих малой энергией, не изменяется и только участок функции распределения, соответствующий электронам с достаточно высокой энергией, сдвигается в сторону еще больших´ энергий. В области v vF0 не замечено сколько-нибудь значительных отклонений от кривой, относящейся к случаю T D 0. Но видно также, что уже при малых температурах кривая асимптотически стремится к оси v, так что в принципе газ может содержать частицы, обладающие сколь угодно высокой скоростью (энергией).

а)

б)

в)

Рис. 108. Функции распределения электронного газа в металлическом вольфраме при различных температурах. Предполагается, что на каждый атом приходится один свободный электрон.

200

Средняя энергия и теплоемкость электронного газа. За исключением случая T D 0, электроны электронного газа, как указывалось, могут принимать любое значение скорости, так что их кинетическая энергия может изменяться в широких пределах. Среднее значение этой энергии получают путем подсчета полной энергии системы и деления этой величины на общее число

электронов:

W D WN :

Однако с учетом того, что

ZZ1

Интеграл в уравнении (416) не может быть вычислен точно. Соответствующее разложение в

Таким образом, получаем выражение, которое при 0˚С равно, а при более низких температу-

201