12 Модель атома Бора

12.1 Постулаты Бора

Все эти затруднения были преодолены Нильсом Бором (1913 г.) в его модели атома. В настоящее время эта модель считается лишь первым приближением при решении данной задачи. Но, тем не менее, сила ее наглядности такова, что и сегодня общая теория Бора сохраняет свое значение4.

Теория Бора пользуется при описании явлений классическими понятиями. Речь идет о частицах, движущихся по определенным орбитам, протяженность которых в пространстве точно определяется или, по крайней мере, принципиально определима. Новое по сравнению с классической механикой заключается в том, что некоторые орбиты или, точнее, формы движения разрешены, а другие запрещены. Дальнейшее развитие теории Бора — квантовая механика, уже отказывается от наглядности такого рода: явления микрофизики и макрофизики не могут быть описаны одной системой понятий, обобщающей макрофизический опыт и поэтому считающейся наглядной. Ведь следует ожидать, что при изменении масштаба на 8–10 порядков мы могли бы встретиться с совершенно новым миром. Поскольку квантовомеханические расчеты используют в качестве отправного пункта картину, даваемую теорией Бора5, эту теорию следует рассмотреть подробно.

Постулаты теории атома Бора гласят:

1. Электроны в атоме могут двигаться вокруг ядра лишь по определенным орбитам. Электроны, двигающиеся по таким орбитам, в противоположность законам классической электродинамики не излучают энергии. В случае круговых орбит их радиус определяется условием, что момент импульса электрона, движущегося по орбите, кратен величине h=2 , т. е.

2. Атом излучает лишь тогда, когда электрон переходит с одной орбиты на другую. Частота излученного света определяется боровским условием частот

Здесь Wn2 — энергия орбиты, определяемой целым числом n2 — квантовым числом; Wn1 — энергия, соответствующая орбите, определяемой квантовым числом n1, a h D 6:6262 10 34 Дж с — постоянная Планка. При перескоке с одной орбиты на другую электрон излучает энергию, равную разности энергий орбит в виде одного фотона. В случае поглощения происходит, естественно, обратный процесс: атом поглощает лишь такой фотон h , который способен поднять электрон с орбиты, соответствующей более низкой энергии, на орбиту с более высокой энергией.

Постулаты Бора не могут быть выведены из более простых предположений, а значит, должны рассматриваться как основные законы. Они сами должны явиться объяснением более сложных явлений. Справедливость постулатов, следовательно, подтверждается не путем прямых логических доказательств, а тем, что выводы, полученные из них, согласуются с экспериментальными фактами.

4Теория Бора сегодня имеет лишь историческое и в какой-то мере иллюстративное значение.

5Квантовая теория использует в качестве основы результаты эксперимента, отчетливо указывающие на присущий микромиру корпускулярно-волновой дуализм и описывающее его волновое уравнение Шредингера, а не довольно непоследовательную и неполную картину, создаваемую теорией Бора. Изучение теории Бора полезно, скорее, в методическом отношении.

101

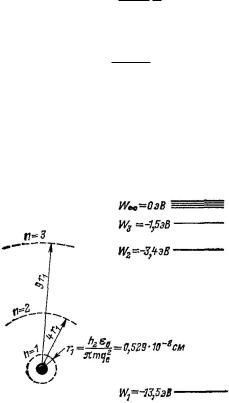
12.2 Возможные энергетические состояния атома водорода

Сначала рассчитаем для атома водорода все возможные радиусы орбит, скорости и частоты обращения. При этом величины, соответствующие различным квантовым числам, будут отмечены индексами.

Равновесие центробежной и кулоновской сил записывается в виде

Рис. 77. Возможные электронные орбиты в атоме водорода (а) и энергетические уровни, соответствующие отдельным орбитам (б).

Необходимо помнить, что эта величина не является частотой излученного света. Следовало бы даже сказать, что эти два значения ничего общего друг с другом не имеют. Частота излучения требует особого рассмотрения, так как электрон при движении на подобной квантовой орбите вообще не излучает. Правда, ниже будет показано, что все же для больших значений имеет место асимптотическая связь между классической и квантовой частотой.

Формула для rn позволяет установить, что радиусы отдельных орбит относятся друг к другу как квадраты целых чисел. Теперь определим возможные энергетические уровни. Полная энергия

102

Кинетическая и потенциальная энергии могут быть отдельно рассчитаны:

Формула показывает, что полная энергия обратно пропорциональна квадрату квантового числа. А это значит, что возможными являются лишь состояния с дискретными значениями энергии.

На рис. 77 изображены энергетические состояния или энергетические термы. В случае атома водорода только эти энергетические состояния возможны.

12.3 Спектр излучения

Энергию излученного фотона можно рассчитать как разность двух энергетических термов

h D Wn2 Wn1;

откуда для частоты излучения получается:

В спектроскопии обычно используется волновое число

называется постоянной Ридберга. Индекс 1 указывает, что при расчете ядро рассматривалось как неподвижное; это может иметь место лишь при условии, что масса ядра бесконечно велика. В случае ядра с конечной массой М вместо массы электрона m следует в расчете использовать выражение для приведенной массы

M

m m C M :

103

Тогда в формулу (93) вместо R1 войдет величина

Если в выражениях (91) и (92) считать первое квантовое число n1 постоянным, а второму квантовому числу n2 придавать целочисленные значения n2 > n1, то получится определенная серия линейчатого спектра.

Если же речь идет не об атоме водорода, а об атоме с порядковым номером Z, т.е. с зарядом ядра Ze, у которого имеется всего лишь один электрон, движущийся в поле ядра, то формулы изменяются, так как в закон Кулона войдет Z, а в выражение энергетического терма Z2. Получающееся выражение имеет вид:

Приведенные выше теоретические закономерности для случая водорода поразительно точно описывают результаты эксперимента.

Даже зависимость постоянной Ридберга от массы ядра задается с такой точностью, что на основании этой зависимости можно заключить о существовании тяжелого водорода — дейтерия.

На рис. 78 и 79 представлены возможные энергетические состояния атома водорода и соответствующие спектральные линии. Можно убедиться, что плотность расположения линий увеличивается у границы серии. К этой границе примыкает непрерывный спектр. Энергия, необходимая для того, чтобы перевести электрон из основного состояния в состояние, соответствующее границе серии, называется энергией ионизации; при этом электрон переводится в положение, бесконечно удаленное от ядра атома. Атом может поглощать и большие порции энергии; в этом случае избыток над энергией ионизации выделится в виде кинетической энергии выбитого электрона.

12.4 Простейшая форма принципа соответствия

Выше уже упоминалось, что существует очень важная в принципиальном отношении связь между частотой света, излучаемого с точки зрения классических законов электроном, движущимся по кругу, и фактическим значением частоты, рассчитываемым на основании правила частот Бора.

Классическое волновое число выражается формулой

Рассмотрим теперь волновое число, соответствующее переходу между орбитами с

В этом случае переходы на n-й уровень соответствуют классической частоте, относящейся к n-й орбите, и частотам ее высших гармоник.

Обобщение этого факта приводит к принципу соответствия Бора: при больших значениях квантовых чисел квантовые законы переходят в классические. Этот принцип может

104