
- •Движение частиц в одновременно действующих электрическом и магнитном полях
- •Движение частиц в одновременно действующих электрическом и магнитном полях значительной протяжённости
- •Возрастание массы при увеличении скорости
- •Эквивалентность массы и энергии
- •Общие следствия из уравнения движения
- •Форма траектории
- •Движение электрона в поле атомного ядра, описываемое классической теорией
- •Аналоги оптического закона преломления в электрическом и магнитном полях
- •Расчет фокусного расстояния тонкой линзы на основании уравнения движения
- •Электростатическое поле как спектрометр
- •Магнитное поле как спектрометр
- •Каскадный генератор
- •Синхротрон и синхрофазотрон
- •Микротрон
- •Максимальная энергия, достижимая с помощью ускорителей
- •Характеристика диода в высокочастотном поле
- •Фазовая фокусировка
- •Излучающий электрон с точки зрения классической электродинамики
- •Излучение Черенкова
- •Постулаты Бора
- •Спектр излучения
- •Простейшая форма принципа соответствия
- •Модель атома Бора-Зоммерфельда
- •Недостатки теории Бора
- •Аналог волновой оптики
- •Правила вычисления вектора состояния
- •Математические основы квантовой механики
- •Временное изменение ожидаемого значения
- •Роль коммутативности операторов
- •Наиболее важные операторы
- •Система с одним электроном
- •Поведение одноэлектронной системы в магнитном поле
- •Влияние магнитного момента ядра на энергетические состояния атома
- •Понятие микросостояния в квантовой механике
- •Определение распределения, соответствующего состоянию равновесия
- •Связь с макроскопической термодинамикой
- •Классический газ
- •Электронный газ
- •Фотонный газ
- •Природа химической связи
- •Строение твердого тела
- •Распределение потенциальной энергии в металле
- •Зонная теория твердого тела
- •Электроны в периодическом потенциальном поле. Одномерный случай
Аннотация
Курс «Теория электромеханических и компьютерных систем» на стадии получения квалификации бакалавра призван дать студентам основы знаний в названной области. Цель курса состоит в обучении студентов основам применения методов классической и квантово-механической моделей для решения прикладных задач анализа и синтеза электромеханических и компьютерных систем. Общая дисциплина «Теория электромеханических и компьютерных систем» расширяет научный кругозор будущих специалистов по прикладной математике и физике, знакомит с важными классами задач компьютерной техники, теории и практики ускорительных систем, систем управления пучками заряженных частиц. Названная дисциплина находит широкое практическое применение в различных областях техники.

Введение
Ниже будет рассмотрено движение заряженных частиц в электрических и магнитных полях в вакууме. Часть пространства, в котором движутся частицы, создается или в виде запаянного после создания в нем вакуума сосуда или с помощью устройства, снабженного различными уплотнениями, кранами и т.д., обеспечивающего постоянную откачку протекающего воздуха. Необходимая степень разрежения составляет 10 4 10 6 Торр.
Гравитационной силой, действующей наряду с электрическими и магнитными силами, можно пренебречь, так как она на много порядков меньше последних. Если массу частицы обозначим m, а заряд — q, то действующая на частицу сила в электрическом
поле |
|
E |
|
|
E |
|
|
|
|
E |
и в магнитном поле B выражается формулой |
||||||
|
|
|
|
|
E D |
|
E C |
E E |
|
|
E |
E |
E |
F |
qE |
qŒv B ; |
|
Здесь |
E |
|
с/м2. |
|
||||
|
|
F |
, Н; E, В/м; q, А с; v, м/с B, В |
|
||||
Движение частицы под действием этой силы описывается классическим законом
d.mv/E |
qE |
qŒv B ; |
dt |
D E C |
E E |
утверждающим, что изменение импульса за единицу времени равно силе. В такой формулировке закон движения справедлив и для релятивистской области, т.е. и для случаев, когда v ! с (где c — скорость света) и m — непостоянна. При малых скоростях, когда m может быть отождествлена с массой покоя m0, это уравнение справедливо и в другой форме:
|
|
dt D |
E C |
E E |
|
||
E E |
m |
d vE |
|
qE |
qŒv |
B : |
(1) |
|
|||||||
|
|
|
|
|
|
|
|
E и B в общем случае являются функциями координат и времени: |
|
||||||
E |
D E E |
I |
E D |
E E |
|
||
E E.r ; t / |
B B.r ; t /: |
|
|||||
Понятно, что интегрирование уравнения движения возможно только тогда, когда E
E
и E известны. Задача упрощается, если E и E не зависят от времени и их изменение
B E B
в пространстве выражается простым законом. В дальнейшем мы сначала рассмотрим движение в простых полях. Затем постепенно перейдем к более сложным полям.
В проводимых рассуждениях обратное влияние частиц на поле принципиально не учитывается; в частности здесь не учитываются поправки, связанные с электромагнитным излучением, возникающим вследствие ускоренного движения заряженной частицы.
2
1Энергетические характеристики объекта в электромагнитном поле
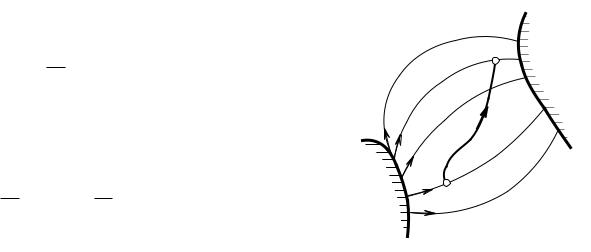
Точное описание процесса движения на основании уравнений движения может быть очень сложным и тогда, когда временное´ изменение полей не учитывается (как правило, так поступают когда речь идет о слабоменяющихся во времени полях, иначе говоря, квази-стационарных). Т.е. когда напряженности полей являются функциями только радиус-вектора rE. Несмотря на это, не строя специальных предположений относительно структуры поля и не рассматривая подробно само движение, можно вывести соотношение для энергии движущейся частицы. Предположим, что частица в течение интервала времени от t1 до t2 движется между точками P1 и P2 по выбранной траектории (рис. 1)
Проинтегрируем обе части уравнения (1) вдоль указанного отрезка:
|
Z |
|
dt |
|
E D |
|
|
Z |
E |
|
E C |
Z |
|
E E E |
|
|
|
|
|||||
|
P2 |
|
d vE |
|
|
|
|
|
P2 |
|
|
|
P2 |
|
|
|
|
|
|
|
|
||
|
P1 |
m |
d r q Ed r q Œv |
|
B d r : |
|
|||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
P1 |
|
|
|
P1 |
|
|
|
|
|
|
|
|
|
|||
Левую часть этого уравнения можно переписать в |
|||||||||||||||||||||||
форме: |
|
Z |
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
||||
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
P2 |
|
|
v2 |
|
d rE |
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|
|||
m |
d vE |
d r |
|
m |
d v |
|
|
mvd v |
|
|
1 |
mv2 |
|
|
1 |
mv2 |
: |
||||||
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||
|
dt |
E D |
|
|
dt |
E D |
|
|
E D |
2 |
|
2 1 |
|
||||||||||
P1 |
|
v |
1 |
|
|
|
|
|
|
v |
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Первое слагаемое правой части выражается сле- |
|||||||||||||||||||||||
дующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
P2 |
|
|
|
|
P2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
q |
Ed r |
|
|
|
|
|
grad Ud rE D |
. |
U1 |
U2 |
/ |
q: |
|
|||||||||
|
Z |
E E D q Z |
|
|
|
||||||||||||||||||
|
P1 |
|
|
|
|
|
P1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
E |
P2 |
|
B |
|
|
|
|
P1
E
E
Рис. 1. Движение заряженной частицы в электростатическом и магнитном полях, действующих одновременно.
U1 и U2 — это, соответственно, потенциалы электрического поля в точках P1 и P2.
Второе слагаемое правой части равно нулю: векторы vE и rE — параллельны, а следовательно, значение смешанного произведения равно нулю. В результате получим:
|
1 |
mv12 |
mv22 D q .U1 U2 |
/ |
|
||
|
|
|
|||||
или |
2 |
|
|||||
|
1 |
mv12 C qU1 D |
1 |
mv22 C qU2 |
; |
(2) |
|
|
|
|
|||||
|
2 |
2 |
|||||
что является законом сохранения энергии.
И левая и правая части представляют собой полную энергию частицы, т.е. сумму ее кинетической и потенциальной энергий в точках P1 и P2. Магнитное поле не вошло в это соотношение, т.е. магнитное поле может изменить только траекторию, а не скорость, так как сила, обусловленная воздействием магнитного поля в любой точке ортогональна траектории.
3

Если известен потенциал, то (2) можно использовать для определения скорости частицы в любой точке пространства:
v2 D r |
2q.U1 U2 |
/ |
v12 |
(3) |
||||
m |
|
|||||||
И если принять, что разность потенциалов между двумя точками U1 |
U2 D U и |
|||||||
начальная скорость частицы в точке P1 равна нулю, то |
|
|||||||
|
|
|
|
|
|
|
|
|
v2 D r |
2q |
|
|
|
||||
|
U |
|
|
(4) |
||||
m |
|
|
||||||
Скорость в любом статическом электрическом и магнитном поле может быть рассчитана по формуле (3), или если начальная скорость равна нулю, то по формуле (4).
Из сказанного следует, что энергия заряженной частицы может быть найдена по значению скорости с помощью формулы 12 mv2 или, когда известна разность потенциалов,
ускоряющая частицу (ускоряющее напряжение), с помощью формулы qU .
Если известно, что частица обладает определенным зарядом, то ускоряющее напряжение однозначно характеризует энергию частицы. Это делает целесообразным введение новой единицы энергии. Самой употребительной единицей измерения работы и энергии в электронике является электронвольт (эВ). 1 эВ — это энергия, которую получает частица, обладающая зарядом e D 1:6 10 19 Кл (т.е. модуль заряда электрона) при прохождении разности потенциалов в 1 В. Отсюда следует:
|
1 эВ D 1:6 10 19 Дж |
|
|
|||
1 Дж D |
|
|
1 |
эВ D 6:24 |
1018 |
эВ |
|
|
|
||||
1:6 |
|
10 19 |
||||
|
|
|
|
|
|
|
4
2Движение частиц в однородном электрическом статическом поле
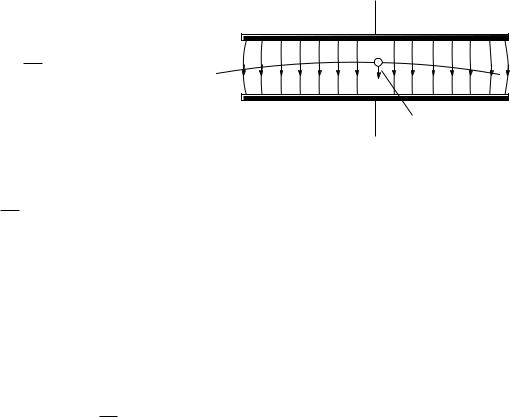
Рассмотрим случай с произвольной начальной скоростью. Будем рассматривать простейший случай: однородное электрическое поле. Поле, близкое к однородному, создается между двумя плоскими поверхностями большой протяженности (рис. 2).
На частицу с зарядом q и массой m |
|
qE, так что уравнение дви- |
|
действует сила E |
C |
жения имеет вид: |
m |
d vE |
D |
qE: |
|
dt |
E |
Величина q включает в себя знак заряда частицы. Направление и величина ускорения постоянны, так как, по нашему
предположению, поле E — постоянно:
E
vE
E D E
F qE
Рис. 2. Сила, действующая на частицу в поле
d v |
|
|
E |
конденсатора. |
|
E |
a |
q |
E |
: |
|
dt |
m |
||||
D E D |
|
|
Таким образом, для любого момента времени t скорость имеет вид:
vE D vE0 C tZ0 |
t |
|
E |
|
E |
|
|
|
|
|
|||
|
E |
E |
|
|||
|
q |
|
dt D q |
|
.t t0/ C vE0; |
|
|
m |
m |
||||
если в момент t D t0 частица имела скорость v D v0. Радиус-вектор частицы выражается в форме:
E E 0 |
D tZ0 |
dt |
D tZ0 |
E D |
|
m tZ0 |
|
0 |
C E0 tZ0 |
||
|
t |
|
|
t |
|
|
|
|
t |
|
t |
|
|
|
|
|
|
E |
|
|
|
||
r r |
|
d rE |
dt |
|
vdt |
q |
E |
|
.t |
t /dt |
v dt |
|
|
|
|
||||||||
Отсюда в конечном итоге получим:
|
1 |
|
E |
|
2 |
rE.t / D |
|
q |
E |
.t |
t0/ C vE0.t t0/ C rE0; |
2 |
m |
при условии, что в начальный момент времени t D t0 радиус-вектор частицы был rE D rE0. В последнем уравнении величина vE0.t t0/ соответствует движению с постоянной скоростью vE0, а первое слагаемое характеризует равноускоренное движение в направле-
нии поля.
Возникающая в результате траектория движения подобна траектории движения тела, брошенного под углом к горизонту с некоторой начальной скоростью.
Выберем систему координат таким образом. чтобы направление поля имело противоположное направление к оси y (рис. 3). Частица должна в момент времени t0 D 0 начать двигаться из исходной точки rE0 D 0 с начальной скоростью vE0. Тогда уравнения движения записываются в виде:
5

y 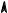
v0y
E
E
q
Ev |
0 |
v0x |
x |
|
Рис. 3. Движение частицы в однородном электрическом поле.
8 |
a |
|
q |
E |
|
|
|
|
|
|
|
|
|
|
|
||||
E |
D |
m E |
I |
|
|
|
|||
q |
|
|
|
v0 |
|
||||
ˆ v |
|
|
Et |
|
|
||||
ˆ |
E |
D |
|
E |
|
C E I |
|
||
ˆ |
m |
|
|
|
|
||||
ˆ |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
ˆ rE |
D |
1 q |
Et 2 |
v |
t |
||||
2 m |
|
E |
C E0 |
|
|||||
ˆ |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
ˆ
:
и могут быть разложены на компоненты:
8 ax |
D 0I |
ay |
ˆ |
D I |
|
ˆ |
|
|
ˆ |
|
|
ˆ |
|
|
< |
|
|
ˆ vx |
v0x |
vy |
ˆ |
|
|
ˆ |
|
|
ˆ |
|
|
ˆ |
|
|
: |
D v0x t I |
y |
ˆ x |
Dq mq EI
|
|
q |
||||
D |
|
|
|
|
Et C v0y I |
|
m |
||||||
|
1 q |
|||||
D |
|
|
|
Et 2 C v0y t: |
||
2 |
m |
|||||
Из этих уравнений можно рассчитать все интересующие нас величины, например, траекторию движения частицы. Два последних уравнения представляют как раз уравнение траектории в параметрической форме. Если переменную t , используя формулу t D x=v0x , исключить из последнего уравнения, то получим:
y D |
1 q E |
x2 |
C |
v0y |
|||||
|
|
|
|
|
|
x: |
|||
2 m v2 |
v0x |
||||||||
|
|
|
|
|
0x |
|
|
|
|
Отсюда видно, что траектория является параболой.
Рассмотрим теперь два особых практически важных случая.
Начальная скорость равна нулю (vE0 D 0). Сначала предположим, что частица стартует из центра системы координат со скоростью vE0 D 0. Тогда уравнения движения имеют вид:
|
q |
|
q |
|
1 q |
|||||
ay D |
|
EI |
vy D |
|
Et I |
y D |
|
|
|
Et 2: |
m |
m |
2 |
m |
|||||||
Это соответствует свободному падению в механике. Если расстояние между пластинами конденсатора равно d , то полная продолжительность полета частицы выражается формулой s
m 1 td D 2d q E :
6
Достигнув нижнего электрода, ускоренная частица сталкивается с ним, передавая ему свою кинетическую энергию, что приводит к нагреванию электрода. Если в электроде вырезано отверстие, то частица будет продолжать дальнейшее движение со скоростью, равной конечной. Так заряженная частица может сохранять заданную ей скорость.
Конечное значение энергии частицы равно:
1 |
mvy2 D |
1 |
m.ay td /2 D |
1 |
m |
q2E2 |
2d |
m |
|
1 |
D qEd D qU |
||
2 |
|
2 |
|
2 |
m2 |
q |
E |
||||||
.
Такого результата следовало ожидать. Ведь произошло превращение потенциальной энергии qU в кинетическую. Конечную скорость легко получить из вышеприведенного уравнения сохранения энергии r
2qU vy D m :
Отсюда следует, что конечные скорости частиц с одинаковым зарядом, но разными массами будут различны.
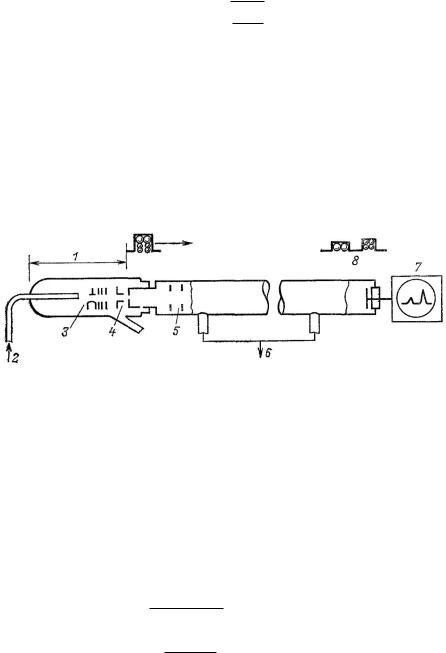
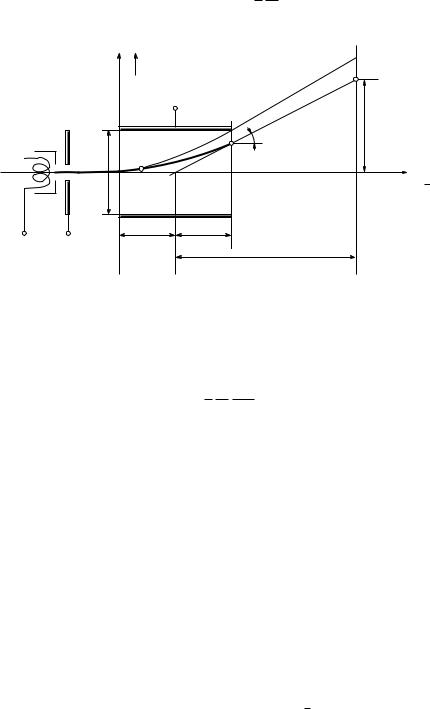
Поэтому если пучок, состоящий из смеси ионов, т.е. ионов с различными массами, ускоряется, как это показано на рис. 4, то отдельные компоненты пучка достигают электрода с различной скоростью и после прохождения через электрод ионы с разными массами разделяются на отдельные группы. Из одного единственного, начального импульса тока образуется, таким образом, ряд последовательно достигающих электрода импульсов. Этот весьма простой принцип действия положен в основу одного из типов масс-спектрометров.
Рис. 4. Времяпролетный масс-спектрометр. Общая длина трубки приблизительно 3.5 м (по Виллею).
1 – источник ионов, 2 – газ; 3 – ионизирующий электронный ток; 4 – ускоряющие электроды, 5 – фокусирующие линзы, 6 – к насосу, 7 – регистрирующий осциллограф; 8 – регистрируемый импульс
Для оценки порядка таких величин, как скорость, время пролета, найдем скорости двух изотопов с наибольшим отношением масс, а именно ионов водорода с массовым числом 1 (протона) и с массовым числом
|
ими при ускорении разностью потенциалов 10 кВ (m |
1:67 |
|
10 |
27 кг |
I |
m |
d |
||||||||||||||
2 (дейтрона), полученные |
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
p D |
|
|
|
|
|||
2mp I qp D qd D 1:6 10 |
|
Кл): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vp D s |
|
|
1:6 10 19 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
104 D 1:39 106 м=сI |
|
|
|
|
|
|
|
||||||||
|
|
1:67 |
10 27 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
d |
D |
1:39 106 |
D |
0:98 |
|
106 м=с: |
|
|
|
|
|
|
|
||||||
|
|
|
|
p |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, полученные скорости оказались на два порядка меньше, чем скорость света. При таких скоростях ион пролетает расстояние в 1 м за время 1 мкс (10 6 с). Если продолжительность импульса
7
также имеет порядок 10 6 с (1 мкс), то «пучок» из протонов и дейтронов, пройдя несколько метров, уже оказывается пространственно разделенным. При всей принципиальной простоте такой масс-спектрограф слишком велик по размерам.
Начальная скорость ортогональна электрическому полю. В этом случае частица влетает в поле конденсатора с начальной скоростью vox , ортогональной силовым линиям. Это соответствует случаю бросания камня параллельно линии горизонта. Направление поля в этом случае совпадает с направлением оси y. Уравнения движения имеют вид:
|
|
|
|
|
1 q |
|
|
|
|
x D v0x t I |
y D |
2 m Et 2: |
|
|
|
|
|
y |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
Ua |
|
|
|
|
|
|
|
|
|
˛ |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
d |
q |
|
x D l |
x D L C |
l |
|
|
|
|
2 |
||||
Ub |
|
l =2 |
l =2 |
|
L |
|
|
|
|
|
|
|
|||
Рис. 5. Отклонение в поле плоского конденсатора. Пунктирная линия изображает траекторию, соответствующую максимально возможному отклонению.
Отсюда следует уравнение траектории:
y D 1 q E x2:
2 m v0x2
Рассчитаем теперь, как велико вызванное полем отклонение пучка, измеренное на экране, расположенном на расстоянии L от середины конденсатора. После выхода из поля частица движется дальше с постоянной скоростью в направлении, касательном к траектории. Если использовать обозначения рис. 5, то для угла, характеризующего направление траектории в момент выхода частицы из поля, справедливо соотношение:
tg ˛ D |
dy |
xDl |
D |
q E |
x xDl D q |
El |
: |
||
|
|
|
|
|
|||||
dx |
m |
v0x2 |
mv0x2 |
||||||
Так как касательная к параболе в точке x D l пересекает ось в точке x D l =2, то уравнение этой касательной имеет вид:
|
D |
|
|
2 D |
mv0x2 |
|
2 |
||
y |
|
tg ˛ |
x |
l |
|
E |
l x |
|
l |
|
|
q |
|
|
: |
||||
Отклонение (т.е. ордината прямой в точке x D L C 2l ) равно:
8

D D q |
E |
l L: |
|
||
mv0x2 |
Таким образом, отклонение зависит от кинетической энергии частицы, а именно обратно пропорционально ей. Учтем далее, что частицы получили скорость, пройдя ускоряющее напряжение Ub . Тогда
r
2q
v0x D m Ub :
Напряженность поля E между пластинами в хорошем приближении определяется на основании значений отклоняющего напряжения Ua и расстояния между пластинами d : E D Ua=d . Подставляя эти значения в предыдущее уравнение, получим для отклонения формулу:
D D |
1 |
1 |
|
Ua |
|
||
|
|
|
|
|
l L: |
(5) |
|
2 |
d |
Ub |
|||||
Таким образом, отклонение тем больше, чем больше отклоняющее напряжение Ua и чем больше расстояние до проекционного экрана. Стоит отметить, что характеристики частицы .q; m/ в уравнение (5) для отклонения не входят. Поэтому, с помощью устройства, представленного на рис. 5 эти величины не могут быть определены. Отклонение пропорционально приложенному к пластинам напряжению. На этом основано применение изображенного устройства на практике. На этом основано применение изображенного устройства на практике. С незначительными изменениями оно представляет собой важнейший прибор современной электронной измерительной техники — электронный осциллограф.
Электроны, выходящие из подогреваемого катода, фокусируются с помощью системы электрических линз, устройство которых будет еще обсуждаться подробнее, в острый пучок. Эти электроны попадают в поле отклоняющих пластин, где отклоняются так, как было сказано ранее и ударяются о флуоресцирующий экран, создавая там четкую точку. На пути пучка может быть вторая пара отклоняющих пластин, поле которой и вызываемое им отклонение перпендикулярны к полю и отклонению первой пары пластин. Положение светящейся точки на экране позволяет теперь считывать значения двух напряжений. Наиболее положительное качество электронно-лучевой трубки (ЭЛТ) заключается в том, что положение пучка, а значит и смещение световой точки на экране следуют за отклоняющим напряжением в большинстве случаев (но не всегда) практически безынерционно. Вследствие послесвечения экрана (в осциллографах это делают специально) и в силу инерционности восприятия человеческий глаз видит на экране при быстрых изменениях отклоняющего напряжения траекторию движения светящейся точки.
Особенно благоприятная возможность для исследования возникает, если на одну пару пластин подается любой периодический процесс, а на вторую пару — напряжение, прямо пропорциональное времени. Это напряжение линейно растет (как функция времени) от нуля до максимального значения, достигаемого в конце периода, а затем, за время, очень короткое по сравнению с периодом, падает до нуля, после чего снова начинает линейно возрастать. Процессы такого рода носят название пилообразных (релаксационных) колебаний. В результате на экране можно видеть протекание во времени исследуемого явления, как бы нарисованного в координатной системе.
9

Очень важной характеристикой ЭЛТ является их чувствительность, а именно величина отклонения электронного луча, вызываемого изменением отклоняющего напряжения на единицу измерения напряжения (вольт):
D D l L 1 :
Ua 2d Ub
Значение практически достижимой чувствительности можно определить исходя из
данных:
d D 0:5 10 2 мI l D 1:25 10 2 мI L D 0:2 мI
Ua D 30 ВI Ub D 1 кВ:
Тогда получим:
D D 1 1 Ua l L D 0:75 см 2 d Ub
D |
D 0:25 10 |
3 |
м |
: |
|
|
|||
Ua |
|
В |
Если частота очень велика (свыше 109 Гц), все эти представления и полученные значения уже недействительны, так как электронный пучок уже не может рассматриваться как безынерционный.
Измерение удельного заряда электрона. Опыт Милликена позволил определить значение заряда электрона вне зависимости от какого-либо другого значения. Можно попытаться определить массу электрона, используя электростатическое отклонение. Однако в формулу (1) не входят значения, характеризующие частицу, а лишь геометрические размеры и отношение отклоняющего напряжения к ускоряющему. Опыт может быть повторен для любых частиц, отклонение всегда будет оставаться одним и тем же. Если же скорость частицы определить каким-то иным способом, то, зная её, а также зная ускоряющее напряжение, можно найти величину e=m.
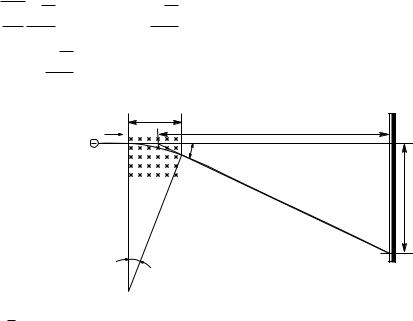
Рис. 6. Измерение удельного заряда электрона (метод Кирхнера).
Измерение скорости можно осуществить так, как показано на рис. 6. Введем пучок электронов, ускоренных напряжением Ub , в поле отклоняющего конденсатора и подведем к паре пластин отклоняющее переменное синусоидальное напряжение очень высокой частоты f . Проходящие электроны в зависимости от направления мгновенной напряженности поля отклоняются попеременно вверх и вниз. Не отклоненными окажутся лишь те электроны, при прохождении которых через конденсатор отклоняющее напряжение было равно нулю. За первой парой пластин на определенном расстоянии
10

расположена вторая пара отклоняющих пластин. Между ними могут пройти лишь те электроны, которые не были отклонены в первом конденсаторе. Если на вторую пару пластин наложить то же самое напряжение, то и они будут отклонять попавшие туда электроны; исключение составят лишь те электроны, которые прошли конденсатор при нулевом значении напряжения. На проекционный экран Д попадают лишь электроны, не претерпевшие отклонения, а именно те, которые прошли расстояние между двумя конденсаторами за интервал времени между двумя прохождениями напряжения через нуль. В простейшем случае это время пролета будет равно:
D T2 D 21f ;
а скорость выразится равенством s
2e |
2L |
|
|
|
Ub D v D |
|
D 2f L: |
me |
T |
||
Выражение для e=me , таким образом, имеет вид:
e |
D |
1 v2 |
D |
2f 2L2 |
: |
||
|
|
|
|
|
|||
me |
2 Ub |
Ub |
|||||
Все величины, входящие в правую часть равенства, могут быть измерены, а значит возможно определение значения e=me . Это значение равно:
mee D 1:759 1011 Кл=кг:
Отсюда, зная е, получают массу электрона:
me D 9:10956 10 31 кг:
Используя эти значения, можно выразить конечную скорость электронов, ускоренных под влиянием разности потенциалов U :
v D 5:931 105pU м=с
Необходимо добавить, что это выражение справедливо лишь для скоростей, малых по сравнению со скоростью света. На практике при напряжениях, превышающих 104 В, необходимо вносить релятивистские поправки, что будет обсуждаться ниже.
11

3Движение частиц в однородном магнитном статическом поле. Фокусировка в магнитном поле
Для силы, действующей на частицу в однородном магнитном поле, можно записать
F |
qŒv B |
D |
m |
d vE |
: |
E D |
E E |
|
dt |
|
Отсюда видно, что сила всегда направлена ортогонально скорости vE. Это означает, что поле влияет лишь на направление, но не на величину скорости частицы. Умножив написанное выше уравнение на vE, получим:
|
|
mv |
d vE |
|
|
E dt |
|
откуда |
|
|
|
|
d.v2/ |
D 0; v2 |
|
|
dt |
||
Ev |
0 |
|
hi
D E E |
B |
D |
0; |
|
|
qv v |
E |
|
|
|
|
D CONST |
) |
|
jEvj D CONST: |
||
E |
|
|
|
|
|
B |
|
|
mv0 |
||
|
|
|
r D |
|
|
|
|
|
qB |
||
Рис. 7. Движение заряженной частицы в однородном магнитном поле (частный случай E ? E). v B
Рассмотрим частицу, начальная скорость которой vE0 ортогональна вектору магнитной
индукции E (рис.??).
B
В этом случае вектор скорости, так же как и вектор силы, лежит в плоскости, пер-
пендикулярной к E, так что движение является плоским, причем действующая сила
B
все время направлена перпендикулярно к скорости, а абсолютная величина скорости постоянна: jEvj D jEv0j. В этом случае движение является равномерным движением по окружности. Ускорение тела, движущегося по круговой орбите выражается формулой v2=r . Тогда уравнение движения Ньютона запишется в следующем виде:
mv2
r
D qvB:
Это уравнение можно рассматривать как условие равновесия между силой F и центробежной силой mv2=r . Теперь можно получить:
r D mqBv :
Отсюда следует, что радиус r пропорционален импульсу частицы. Время оборота выражается формулой:
TD 2 r D 2 m : v qB
12
И тогда частота обращения будет равна |
|
|
|
|
|
|
|
|
|
f D |
1 |
|
D |
qB |
|
; |
|||
|
|
|
|
|
|||||
T |
2 m |
||||||||
а для угловой скорости получим: |
|
|
|
|
|
|
|
|
|
! D |
2 |
D |
qB |
: |
|||||
|
|
|
|
||||||
|
T |
|
m |
||||||
Необходимо отметить, что угловая скорость частицы не зависит от ее линейной скорости, а зависит только от магнитного поля и удельного заряда частицы.
Частица, движущаяся по окружности радиуса r , имеет энергию:
W D 2 mv2 D 2 m m |
D |
2 |
m |
: |
|||
1 |
|
1 qBr |
2 |
1 |
|
q2B2r 2 |
|
Если частица приобрела скорость v, пролетая ускоряющее напряжение U , то
v D r |
|
|
|
|
|
: |
|
||||
|
m U |
|
|||||||||
|
|
|
|
2q |
|
|
|
|
|
||
Тогда |
|
|
|
|
|
||||||
r D s |
|
|
|
|
|
|
|
: |
|||
|
q |
|
|
|
|||||||
|
|
B |
|||||||||
|
|
2m |
|
pU |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, радиус зависит от удельного заряда q=m, т.е. от типа частицы. Если разные частицы ускоряются одним и тем же напряжением, то радиусы орбит частиц окажутся различными. Таким образом, можно обеспечить разделение частиц с разными удельными зарядами. Это принцип действия простейшего масс-спектрометра, который может быть осуществлен на практике.
Для случая нерелятивистских скоростей числовые соотношения имеют следующий
вид: |
|
2m pU |
|
|
pU |
|
||
|
|
|
|
|
||||
— для электрона: |
|
r D s q |
B |
D 3:37 10 6 |
B |
(В единицах СИ); |
||
|
|
|
pU |
|
|
|
|
|
— для протона: |
r D 1:44 10 4 |
B |
(В единицах СИ). |
|||||
С помощью однородного магнит- |
|
|
|
|
||||
ного поля поток частиц (например |
vE |
|
l |
L |
||||
электронов), так же как и в случае |
|
|
||||||
|
|
' |
||||||
электрического поля, можно откло- |
|
|
|
|||||
|
|
|
|
|||||
нять (рис. 8). При не очень большом |
|
|
|
|
||||
угле отклонения справедливо равен- |
r |
B |
|
D |
||||
E |
|
|||||||
ство: |
|
|
|
|
|
|
|
|
D D L tg ' L': |
|
|
|
' |
|
|
||
|
|
|
|
|
|
|||
С другой стороны, при малом угле ' |
|
|
|
|
||||
|
|
l |
|
|
|
|
|
|
r ' l |
) |
' r |
: |
|
Рис. 8. Отклонение в однородном магнитном поле. |
|||
13

|
|
z |
|
|
|
E |
|
|
|
B |
|
d |
|
|
y |
|
|
|
|
d |
v0z |
vE0 |
|
|
|
||
|
|
v0x |
x |
y
Рис. 9. Движение в однородном магнитном поле при условии, что начальная скорость не перпен-
дикулярна E.
B
Тогда
D D Llr D LlB mqv :
Так можно создать электронно-лучевую трубку с магнитным отклонением. В этом случае, отклонение обратно пропорционально импульсу частицы, а не энергии, как это было в электрическом поле.
Теперь рассмотрим общий случай, при котором начальная скорость частицы образует
произвольный угол с E (рис.
B 9).
Разложим vE0 на компоненты v0x и v0z , как показано на рисунке.
Сразу можно понять, что движение частицы происходит по винтовой линии. Компонента v0x способствует круговому движению, в то время как v0z , направленная так
же как и E, никакой силы не вызывает. Таким образом, 0x обеспечивает движение
B v
по окружности, а v0z — равномерное прямолинейное движение ортогонально плоскости круговой орбиты. Обе компоненты скорости вместе дают движение по винтовой линии.
Итак, скорость разлагается на компоненты: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
vE D vEjj C vE?; |
|
|
|
|
|
|
|
|||||||
E |
|
|
|
|
|
E |
|
E |
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
||
где v |
jj |
|
|
|
|
|
|
v? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
— параллельна B, а |
|
|
— ортогональна B. Уравнение движения в этом случае |
|||||||||||||||||||||||
записывается в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
m |
d.vEjj C vE?/ |
D |
qŒ.v |
v |
/ |
|
B |
D |
qŒv |
B : |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
Ejj |
C E? |
|
E |
E? |
E |
|
|
|||||
Так как правая часть этого равенства всегда перпендикулярна к |
B, то справедливы |
||||||||||||||||||||||||||
E |
|
||||||||||||||||||||||||||
выражения |
D |
|
I E D |
|
|
I |
|
|
|
|
D m hE? |
|
i D |
m h |
E?i |
||||||||||||
|
|
|
dt |
0 |
CONST |
|
dt |
B |
|||||||||||||||||||
|
|
|
d vEjj |
|
|
v |
|
|
|
d vE? |
|
q |
|
v |
|
|
q |
B |
v |
: |
|||||||
|
|
|
|
|
|
|
|
jj |
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
E D |
|
m |
E |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Введя вектор круговой частоты ! |
|
|
q |
B, получим: |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
D |
E E? |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
d vE? |
|
|
! |
|
v |
: |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
14
Последнее равенство означает, что проекция частицы на плоскость, перпендику-
лярную вектору магнитной индукции E, движется по круговой траектории с угловой
B
скоростью:
j!E j D jqj mB :
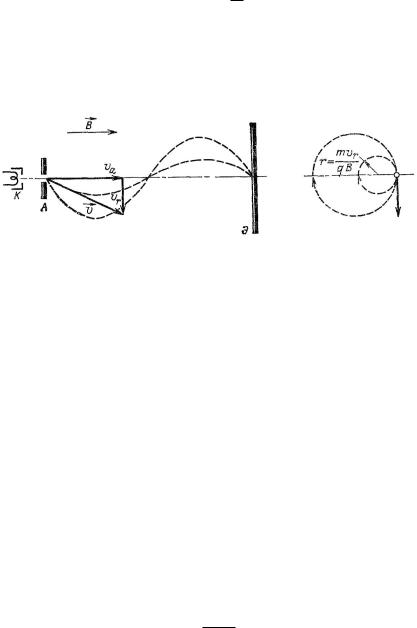
Это движение имеет интересное практическое применение. Электроны, выходящие из катода К и ускоряемые анодом А (рис. 10), выходят из щели анода в виде слаборасходящегося пучка, вследствие чего на экране Э вместо ожидаемой светящейся точки дают круглое пятно. Для исправления этого недостатка создают осевое магнитное поле. Под
Рис. 10. Фокусировка слаборасходящегося пучка электронов.
действием такого поля электроны вынуждены двигаться по винтовой траектории, радиус которой выражается в обозначениях, принятых на рис. 10 формулой
|
r D |
mvr |
|
; |
|
|
|
|||
|
|
qB |
|
|
|
|
||||
а время обращения |
|
|
|
|
|
|
|
|
|
|
T D |
2 r |
|
D |
2 m |
: |
|
||||
|
|
|
|
|
|
|
||||
|
vr |
|
|
qB |
|
|||||
Отсюда следует, что шаг винтовой линии равен |
|
|
|
|
|
|||||
|
|
|
|
2 m |
|
|
||||
d D T va D |
|
va |
: |
|||||||
qB |
||||||||||
Учитывая, что va D v cos ˛, а ˛ 0, можно получить:
d 2 m v: qB
Если значение v одинаково для всех электронов, то значения d и T тоже будут примерно одинаковы.
Электроны движутся по винтовым линиям, проекции которых являются окружностями с различными радиусами. В точках оси, отстоящих друг от друга на расстояние d электроны встречаются вновь.
Описанное устройство фокусирует расходящийся электронный пучок в одной точке. Магнитное поле ведет себя как линза.
15

4Движение частиц в одновременно действующих электрическом и магнитном полях. Движение частиц в одновременно действующих параллельных электрическом и магнитном полях. Движение частиц в одновременно действующих скрещенных электрическом и магнитном полях. Общий случай.
4.1Движение частиц в одновременно действующих электрическом и магнитном полях
При одновременном наложении электрического и магнитного полей оба поля действуют независимо одно от другого, так что можно получить самые различные результирующие движения и в соответствии с этим самым разнообразные возможности применения.
В простейшем случае силы, действующие со стороны электрического и магнитного полей, взаимно ком-
пенсируются. Так получают прибор, создающий однородный по скорости Рис. 11. Устройство, обеспечивающее селекцию ча-
пучок частиц (рис. 11).
Пусть однородное магнитное поле, создаваемое в пространстве между пластинами, перпендикулярно к плоскости рисунка. Если в это пространство попадает пучок, состоящий из частиц, скорости которых различны, то на каждую частицу действует сила
F D q.E vB/:
Если скорость частицы удовлетворяет условию
E v0 D B ;
то в любой момент времени сила равна нулю, так что частица проходит через диафрагму экрана Д. Если же скорость частицы больше или меньше чем v0, то такую частицу сила F отклоняет вверх или вниз так, что она ударяется об экран Д. В результате этого справа от Д будет получаться пучок однородный по скорости. Описанное устройство может быть также использовано для измерения скорости.
Если электрическое и магнитное поля параллельны (рис. 12), то отклонения частицы, вызываемые этими полями, перпендикулярны друг другу.
Отклонение, вызываемое этими полями, как это следует из предыдущего, равно для электрического поля:
xD El L mv2 D A mv2 ;
а для магнитного поля
y D LlB q D C q : mv mv
16
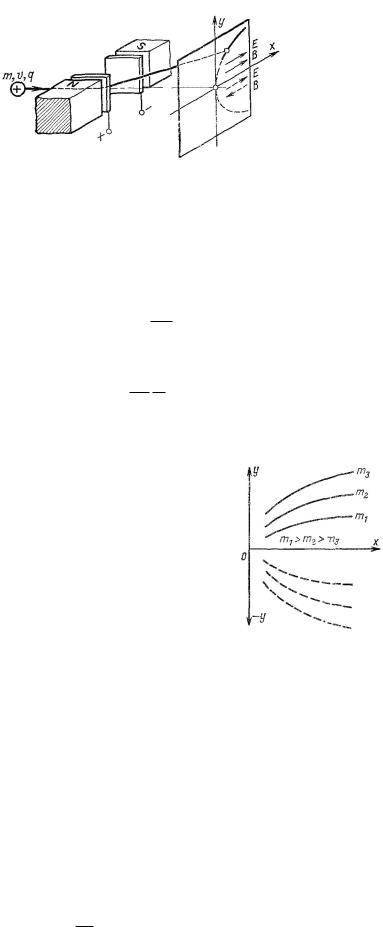
Рис. 12. Схема параболического масс-спектрометра Томсона.
Частицы, обладающие одинаковыми свойствами, т.е. одинаковым удельным зарядом q=m, попадают в зависимости от их скорости в различные точки. Эти точки образуют параболу. В уравнении для магнитного поля
v D C myq ;
подставив полученное выражение в уравнение для электрического поля, имеем
x D A m y2: C 2 q
Величины A и C являются постоянными прибора.
Очевидно, каждому отдельному типу ионов соответствует своя парабола. Отличающиеся друг от друга ионы, имеющие различные скорости, разделяются в этом устройстве, а именно, ионы с одинаковым удельным зарядом и любым значением скорости попадают на отдельную ветвь параболы, вызывая почернение на фотопластинке. Подобное семейство кривых изображено на рис. 13.
По координатам любой точки параболы можно однозначно определить значение q=m.
Рис. 13. Кривые, полученные методом парабол.
4.2Движение частиц в одновременно действующих электрическом и магнитном полях значительной протяжённости
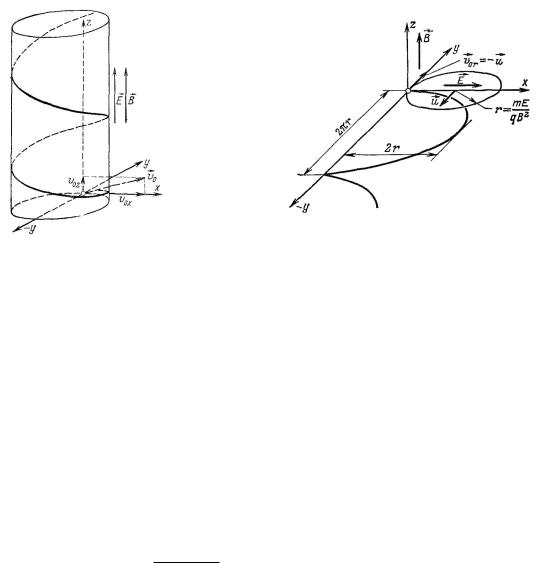
Определение траектории. Если частица не покидает, как это рассматривалось выше, однородное электрическое и магнитное поля, а движется в них постоянно, то магнитное поля вынуждает её двигаться по окружности в плоскости, перпендикулярной к направлению поля, а электрическое поле ускоряет её. В результате получается винтовая линия с увеличивающимся шагом (рис. 14).
На рис. 15 показан случай, когда E и E взаимно перпендикулярны и частица стартует
E B
из начала координат с начальной скоростью, равной нулю. Уравнение движения в этом
случае имеет вид: |
D |
E C E E |
|
|
dt |
||
m |
d vE |
|
q.E Œv B /: |
|
|||
17
|
Рис. 15. Движение заряженной частицы во взаимно |
Рис. 14. Движение в параллель- |
перпендикулярных электрическом и магнитном полях |
ных однородных электрическом |
при начальной скорости, раной нулю. |
и магнитном полях. |
|
Выберем теперь новую систему координат, оси которой в момент времени t D 0 совпадают с осями старой системы, причем новая система движется с постоянной скоростью uE относительно старой.
Скорость частицы, измеренная в неподвижной системе координат, в любой момент времени может быть представлена формулой
vE D uE C vEr ;
где uE — скорость движущейся системы координат, а vEr — относящаяся к ней скорость, т.е. относительная скорость, измеренная в движущейся системе координат. Если это выражение подставить вместо vE в уравнение движения, то получим:
m |
d.uE C vEr / |
|
q.E |
Œu B |
Œv |
r |
B /: |
|
|
dt |
D |
E |
C E |
E |
|
E |
|
|
|
|
C E |
|
||||
Введение движущейся системы координат пока вело лишь к усложнениям. Но можно выбрать значение скорости uE, до сих пор еще неопределенное, таким, чтобы движение в перемещающейся системе координат описывалось как можно проще.
С этой целью выберем такое uE, чтобы два первых члена в скобке были равны нулю,
т.е.
E C E E D
E Œu B 0:
Отсюда следует, что скорость uE должна быть направлена в сторону отрицательной оси y (рис. 15) и иметь значение
u |
j Ej |
|
E ; |
|||||
j Ej D |
|
E |
|
D |
|
|
|
|
j Ej |
B |
|
||||||
|
|
B |
|
|
|
|
|
|
т.е. |
j E |
|
Ej : |
|||||
u |
||||||||
j Ej D |
|
E |
|
B |
||||
|
B2 |
|
|
|
|
|||
Тогда в движущейся системе координат уравнение движения будет иметь вид:
|
|
D |
|
r |
E |
|
dt |
|
|||
|
E |
B ; |
|||
m d vE |
|
qŒv |
|
||
18

так как производная постоянной величины uE равна нулю.
Частица в движущейся системе координат ведет себя так, как будто теперь существует только магнитное поле. Воздействие электрического поля учтено теперь поступательной скоростью выбранной системы координат.
В движущейся системе координат частица описывает круговую траекторию в том
случае, если E0r перпендикулярно к E, и если система совершает равномерное по- v B
ступательное движение. Поэтому в исходной системе координат траектория является циклоидой.
Угловая скорость движения по окружности и радиус равны соответственно:
! D |
qB |
I |
r D |
mv0r |
: |
m |
qB |
Определение vE0r , входящей в формулу для радиуса, требует некоторых пояснений. Свяжем себя мысленно с движущейся системой координат. Мы знаем, что в момент времени t D 0 частица находилась в начале двух совпадающих в тот момент координатных систем и при наблюдении из покоящейся системы обладала начальной скоростью, равной нулю. Если наблюдать из движущейся системы координат, то скорость частицы оказывается равной:
vE0r D E u;
т.е. совпадает со скоростью движущейся системы относительно неподвижной, но имеет противоположное направление. Для движущегося наблюдателя эта скорость и дальше будет оставаться точно такой же, так как в этой системе действует только магнитное поле, которое не может изменить скорости. Поэтому справедлива формула
r D muqB D qBmE2 :
Так как скорость частицы на окружности |
|
|
|
|||
|
mE qB |
E |
|
|||
r! D |
|
|
|
D |
|
D u |
qB2 |
m |
B |
||||
совпадает со скоростью поступательного движения, то траектория представляет собой циклоиду.
Если наблюдаемая в неподвижной системе координат скорость частицы vE0 в момент времени
D была отлична от нуля и перпендикулярна к E, то ее начальная скорость в системе координат, t 0 B
движущейся со скоростью u D E=B, в которой действует только магнитное поле, выразится формулой
vE0r D vE0 E u:
Эта скорость в движущейся системе остается постоянной. Радиус круговой траектории равен:
r D v!0r D qBm jEv0 E uj;
Относительно результирующего движения можно установить следующее. Частица движется равномерно по окружности радиуса
m
r D qB jEv0 E uj;
19
а сам круг в это время совершает поступательное движение со скоростью
u D
E
B
в отрицательном направлении оси y. Чтобы это представить, следует построить окружность радиусом r , имеющую в начале координат касательную vE0r E u и провести через ее центр прямую, параллельную оси y. По ней перемещается центр базисного круга радиусом
mE r0 D qB2 :
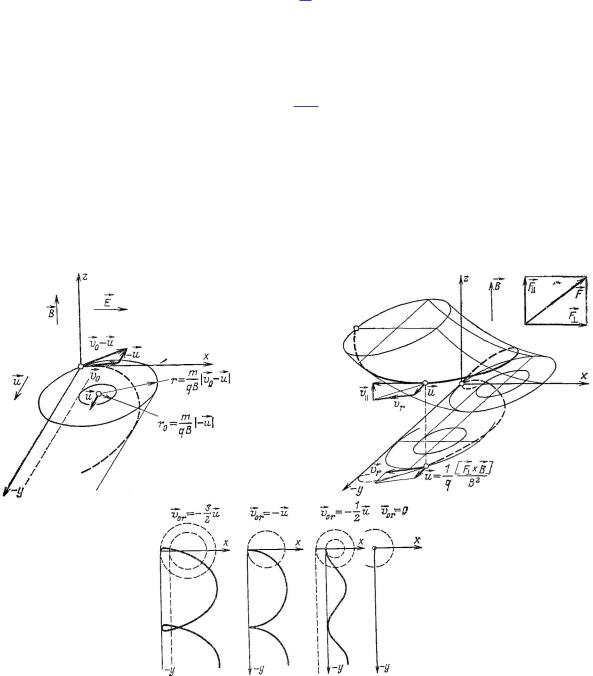
Свяжем жестко оба круга и представим кругу с радиусом r0 возможность катиться по прямой, отстоящей на расстоянии r0 от центра и параллельной оси y. Тогда точка круга с радиусом rE будет описывать искомую траекторию (рис. 16,а). В зависимости от соотношения между r и r0 будут получаться циклоиды различного типа:
при r > r0; т.е. jEv0 E uj > u; — переплетающаяся циклоида; при r D r0; т.е. jEv0 E uj D u; — циклоида с пиками;
при r < r0; т.е. jEv0 E uj < u; — растянутая циклоида (рис. 16,б).
а) |
в) |
б)
Рис. 16. Построение траектории в общем случае (a); траектории, соответствующие разным начальным скоростям (б); движение под воздействием однородного магнитного поля и постоянно действующей силы (в). В случае переплетающейся циклоиды uE0 D 12 uE; циклоиды с пиками vE D 0; растянутой циклоиды vE0 D 12 uE; в последнем случае vE0 D uE.
Непосредственное интегрирование уравнения движения, разложенного на компоненты, не представляет никакой трудности, но при этом теряется наглядность.
Уравнение движения в векторной форме эквивалентно двум скалярным уравнениям
m |
d 2x |
D qE C q |
dy |
BI |
d 2y |
D |
dx |
|
||
|
|
m |
|
q |
|
B: |
||||
dt 2 |
dt |
dt 2 |
dt |
|||||||
20

Второе уравнение легко интегрируется
dy |
|
|
B |
|
|
|
D |
q |
|
x C v0y |
D !x C v0y ; ! D qB=m: |
dt |
m |
||||
Начальное значение dy=dt D vy мы уже учли при определении постоянных интегрирования. При подстановке этого выражения в первое уравнение получим уравнение для определения
x D x.t /: |
d 2x |
qE |
|
|
|
|
C !2x D |
|
C !v0y : |
|
dt 2 |
m |
||
Общее решение этого уравнения слагается из общего решения однородного и частного ре-
шения неоднородного уравнения: |
|
|
|
|
|
|
||
|
|
|
|
|
qE |
v0y |
|
|
x D C1 sin ! t C C2 cos ! t C |
|
C |
|
: |
||||
!2m |
! |
|||||||
Таким образом, для dx=dt получим: |
|
|
|
|
|
|
||
|
dx |
|
|
|
|
|
|
|
|
|
D C1 |
! cos ! t C2 |
! sin ! t: |
|
|
||
|
dt |
|
|
|||||
Используя начальные значения t D 0I x D 0I y |
D 0I |
vx |
D vx0I vy D vy0; нетруд- |
|||||
но определить константы. Если известна функция x D x.t /, то можно с помощью уравнения dy=dt D !x C v0y легко найти y D y.t /. Конечный результат записывается в виде
|
vx0m |
|
|
|
qB |
|
|
vy0m |
|
|
|
mu |
1 |
|
|
qB |
|
|
|
||||||||||
x.t / D |
|
sin |
|
|
t C |
|
|
|
|
|
C |
|
cos |
|
|
t |
I |
|
|
||||||||||
qB |
m |
|
qB |
|
|
qB |
m |
|
|
||||||||||||||||||||
|
|
vx0m |
|
|
|
qB |
|
|
|
vy0m |
|
mu |
|
qB |
|||||||||||||||
y.t / D |
ut |
|
|
|
|
1 |
|
cos |
|
|
|
t C |
|
|
C |
|
sin |
|
t: |
||||||||||
|
qB |
|
m |
qB |
qB |
m |
|||||||||||||||||||||||
Подставляя vx0 D vy0 D 0, находим |
1 |
|
|
|
|
|
|
|
|
|
D r0.1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
mu |
|
|
|
|
qB |
|
|
|
|
|
|
|
|
|||||||||||||
|
x.t / D |
|
|
cos |
|
|
t |
cos ! t /I |
|
|
|
||||||||||||||||||
|
qB |
m |
|
|
|
||||||||||||||||||||||||
|
y.t / D ut C |
mu |
qB |
t D |
ut C r0 sin ! t |
|
|
|
|||||||||||||||||||||
|
|
sin |
|
|
|
|
|||||||||||||||||||||||
|
qB |
m |
|
|
|
||||||||||||||||||||||||
— это уравнение циклоиды с пиками.
Для обобщения задачи о движении в однородном электрическом и магнитном полях следует
E
предположить, что на частицу с массой m и зарядом q одновременно с однородным полем B
действует также и постоянная сила E, которая хотя до сих пор и рассматривалась как сила
F
электрического происхождения, но в общем может быть, например, и гравитационной силой. Тогда уравнение движения запишется в виде
|
d v |
|
|
q |
|
E E |
|
F |
|
|||
|
dt |
D m |
|
C m |
||||||||
|
E |
|
|
|
Œv |
B |
|
E |
: |
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
B: |
Разложим скорость на компоненты параллельную и перпендикулярную к линиям E |
||||||||||||
|
|
d v |
|
|
E |
|
|
|
||||
|
|
|
|
Ek |
D |
F |
k |
|
|
|
||
|
|
|
dt |
|
m |
; |
|
|||||
E |
|
|
|
|
|
|
|
|
B не имеет составляющей в направлении B. Другое уравнение имеет вид: |
||||||||
поскольку Œv E |
|
|
|
|
E |
|
||
d v |
|
q |
|
|
E |
|
||
|
E? |
|
Œv B |
|
F |
? |
; |
|
|
D m |
C |
|
|||||
|
dt |
E? E |
m |
|
||||
21

так как |
E |
|
E |
Œv |
D E |
||
E? |
B |
B : |
|
|
Œv |
Уравнение для Ek определяет ускорение движения в направлении E. Для решения последнего v B
уравнения введем уже известным способом систему координат, движущуюся со скоростью uE:
|
|
|
|
|
vE? D uE C vEr ; |
|
|
|
|
|
|
|
|||
где u и v |
|
|
|
|
|
|
B, т.е. uB |
|
vB |
D |
0; тогда |
||||
E E лежат в плоскости перпендикулярной к |
E |
|
E E |
D E E |
|
||||||||||
d vr |
|
q |
|
|
q |
|
|
|
|
F |
|
|
|
||
|
|
|
|
|
|
|
E |
|
|
||||||
|
E |
|
|
Œu B |
|
|
Œv |
B |
|
|
? |
0: |
|
||
|
|
|
|
|
|
|
|
||||||||
|
dt |
D m E |
E |
C m |
r |
E |
|
C m D |
|
|
|||||
|
|
E |
|
|
|
|
|||||||||
В результате выбора соответствующего uE опять остается одно лишь магнитное поле. Следо-
вательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
Œu B |
|
F |
|
|
|
|
|
|
|
|
|
B |
|
F |
|
0: |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
E? |
|
|
|
|
|
|
|
|
|
|
|
|
E? |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
0 |
|
Œu |
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
m E |
|
C m D |
I |
|
|
C q |
D |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
Умножая векторно первое из двух последних уравнений на B=B2, получаем: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
" B2 |
E |
|
|
E |
# D |
|
Π|
|
qB2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
Œu |
B |
|
|
|
|
E? |
E |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
B |
|
|
|
|
|
|
|
|
|
|||||
или после разложения левой части |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
E E u |
|
E E B |
|
|
|
|
E? |
E : |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
BB |
E |
|
uB |
|
E |
D |
|
ŒF |
|
|
|
B |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
B2 |
|
B2 |
|
|
|
|
|
qB2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение этого уравнения имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u |
1 |
|
Π|
E? |
|
E ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
E D |
|
|
|
F |
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
qB2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
так как E E |
D |
|
E? D |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E D |
E |
E |
|
|
|
|
|
||
uB |
|
0. Если F |
|
|
qE, получим уже известное уравнение: u |
ŒE |
B =B2. |
|
|
|||||||||||||||||||||||||||||||
Для результирующего движения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
vE D vEk C uE C vEr : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ek |
|
|
|
|
|
|
|
|
E |
|
|
|
1 F |
B |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
B2 |
|||||||
Здесь учтены ускорение, сообщаемое силой F |
|
в направлении B, смещение |
|
|
ΠE? E |
, |
||||||||||||||||||||||||||||||||||
перпендикулярное к |
F и B, а также движение по окружности, перпендикулярной к B (рис. 16,в). |
|||||||||||||||||||||||||||||||||||||||
E |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
||||||
Основные соотношения для плоского магнетрона. Электрическое поле в этом случае создается между двумя металлическими пластинами, отстоящими на расстоянии d друг от друга, к которым приложено напряжение U . Одна пластина должна испускать электроны, не имеющие начальной скорости. В соответствии с вышесказанным они движутся по циклоидальной траектории. Радиус траектории рассчитывается по формуле
r D mE D mU : B2q B2qd
Может ли в этом случае наблюдаться анодный электронный ток? Если напряжение мало, то и высота циклоиды будет незначительной. При повышении напряжения
22
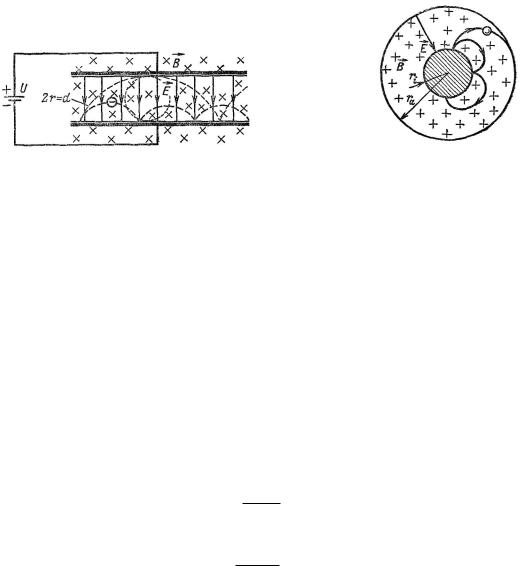
Рис. 17. Условие прохождения тока в плоском магнетроне.
Рис. 18. Устройство для измерения индукции B. Анодное напряжение повышается до тех пор, пока не возникает ток. Прибор, измеряющий напряжение, может калиброваться непосредственно в единицах B.
достигается критическое значение, при котором электроны как раз достигают анода. Наоборот, если анодное напряжение поддерживается постоянным, то анодный ток можно получить лишь при очень малых значениях напряженности магнитного поля. При повышении напряженности магнитного поля сила тока падает до значения, равного нулю, когда магнитное поле становится достаточно сильным, чтобы, искривляя траекторию, вернуть электроны на катод.
На рис. 17 иллюстрируются условия прохождения тока
2r > d;
т.е.
2mU
B2qd > d:
В предельном случае
2mUкр D d 2: Bкр2 q
Отсюда можно рассчитать любую входящую в формулу величину, если все прочие известны.
Принципиально это устройство пригодно и для измерения магнитной индукции; в виде цилиндрического магнетрона оно применяется для этих целей на практике. Напряжение повышается до тех пор, пока не начнет наблюдаться ток. В этом случае имеет
место соотношение |
|
|
|
|
|
||
|
s |
|
|
|
|
|
|
1 |
2mU |
кр |
|
|
|||
Bкр D |
|
|
|
: |
|||
d |
|
q |
|
||||
Ниже кратко обсуждается движение электрона в цилиндрическом магнетроне (рис. 18).
В этом случае поле неоднородно; для напряженности электрического поля справедливо соотношение
E |
D |
d U |
e |
|
UA |
|
1 |
e : |
||
dr |
|
|
|
|
r |
|||||
E |
E D |
|
ri |
|
E |
|||||
|
|
|
r |
ln |
|
|
r |
|||
|
|
|
|
|
ra |
|
|
|
|
|
23

|
Из соображений целесообразности вводятся цилиндрические координаты; тогда для ускоре- |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ния выкладок можно записать: |
|
|
P |
|
|
|
! Er C |
|
|
|
|
|
|
P P C |
|
|
|
|
|
R E' D |
|
|
|
|
|
|
|
E C E |
|
E |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt D |
|
|
|
|
dt 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d vE |
|
|
|
|
|
|
|
|
d 2r |
|
r ' |
2 |
|
|
|
|
e |
|
|
|
|
|
|
|
.2r ' |
|
|
|
|
|
|
r '/e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
.E Œv |
B /: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Далее справедливы равенства |
|
E I |
|
|
|
|
|
|
E |
|
|
|
|
|
D |
|
|
|
|
|
E I |
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
D |
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E D E C |
v |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
ŒB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
vr er |
|
|
' |
|
|
|
' |
|
|
|
|
|
|
ΠE |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
|
|
|
Ber ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
позволяющие переписать уравнение движения в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2r |
|
|
r 'P2 D |
|
e d U |
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e d U |
|
|
|
e d' |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v' B D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
BI |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt 2 |
|
m |
|
|
|
dr |
m |
m |
|
|
dr |
m |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2' |
|
C |
|
|
|
|
dr d' |
|
D |
e |
|
|
|
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt 2 |
dt |
dt |
m |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее уравнение можно записать следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.r 2'/P D |
|
|
|
|
|
B |
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
dt |
m |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
В результате интегрирования получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 2'P D Z |
|
|
e |
|
|
|
|
dr |
|
|
|
|
|
C C D |
|
|
|
e |
|
|
|
2 C C: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Br |
|
|
|
|
dt |
|
|
|
|
|
|
|
|
Br |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
dt |
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пусть электрон стартует от внутреннего цилиндра, так что 'P D 0; r D ri . Тогда постоянная |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
С выразится как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C D |
|
|
|
|
|
|
Bri2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
и предыдущее уравнение примет вид: |
|
|
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 2'P D |
|
|
|
|
e |
|
|
B.r 2 |
|
|
ri2/; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
'P D |
|
|
|
|
|
|
|
|
|
B |
1 |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Подставляя это соотношение в еще не использованное исходное уравнение, получаем: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dr 2 |
|
|
|
|
e2B2 |
|
|
|
2r 2 |
|
|
|
|
|
r 4 |
|
|
|
|
|
|
|
e U |
|
|
|
1 eB2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.r 2 |
|
ri2/ |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ri |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt 2 D |
|
4m2 |
|
|
|
|
|
|
r |
|
|
|
|
|
|
C r 3 ! |
|
|
|
|
|
|
m " ln |
ra |
|
|
|
r |
|
C 2m r |
|
|
|
|
|
|
|
|
|
|
# |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Умножение обеих частей на 2r и интегрирование приводит к равенству |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
D |
|
|
|
|
|
" |
|
|
|
|
2ri |
ln r |
|
|
|
|
|
|
|
|
|
|
|
|
# |
|
|
|
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
ln r C |
|
|
|
|
|
|
|
|
|
|
ri |
ln r !# C C: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
dt |
|
2m2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
2r 2 |
|
|
|
|
|
|
|
|
|
|
m |
ln |
ri |
|
|
|
2m |
|
|
2m |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
dr |
|
|
2 |
|
e2B2 |
r 2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 4 |
|
|
|
|
|
|
|
|
|
|
2e |
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eB2 |
|
|
|
r 2 |
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Учитывая вновь условия начала движения, а именно rP D 0 при r D ri находим |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
D |
|
|
|
" |
|
|
|
|
|
|
|
|
|
|
2ri ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!# |
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
r ln |
|
|
# |
: |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
dt |
|
2m2 |
2 |
|
|
|
|
|
2 |
|
|
|
ri |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
r 2 |
|
|
|
|
|
|
|
r 2 |
|
|
|
|
|
|
m |
|
|
ln |
ri |
|
|
|
|
2m |
2 |
2 |
ri |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
dr |
|
|
|
e2B2 |
|
r 2 |
|
|
|
ri2 |
|
|
|
2 |
|
|
r |
|
|
|
|
|
|
|
|
|
ri4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2e |
|
|
|
UA ln ri |
|
|
eB2 |
|
r 2 |
ri2 |
|
2 r |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Нас интересуют главным образом критические значения, т. е. условия, при которых электрон достигает внешнего цилиндра. Положим rP D 0 при r D ra; тогда из предыдущего равенства можно получить выражение, связывающее Uкр с Bкр:
|
|
eB2кр |
|
|
ri2 |
! |
2 |
|
Uкр |
D |
2 |
1 |
|
||||
|
ra |
|
: |
|||||
8m |
ra2 |
|||||||
|
|
|
|
Этот расчет позволил получить лишь основные формулы для магнетрона.
24
