соотношения, даваемые этой теорией, всегда требуют корректировки для достижения согласованности с экспериментальными данными. Правильный количественный ответ на множество вопросов, не разрешенных теорией Бора, дается в рамках квантовой механики, рассматриваемой ниже; однако достижение этого связано с полным отказом от наглядности, понимаемой в классическом смысле.

12.6 Недостатки теории Бора

Уже было показано, что теория Бора дала объяснение целому ряду явлений. Однако можно выдвинуть два основных возражения против этой теории.

Во-первых, постулат Бора является постулатом типа «deus ex machina»: правила отбора квантованных орбит, противоречащие классическим законам, задаются без всякого обоснования и никак не объясняются. Хотя и оправдывается положение, где каждый основной закон как раз в силу того, что он является основным, принципиально не объяснен и поэтому всегда в известной степени оказывается непонятным; это приводит к постоянной необходимости сведения его к дополнительным, более простым закономерностям. Очевидно, что в рассматриваемом случае квантование носит отпечаток «ad hoc»6 обратного следствия из конечного результата, так что эту теорию с самого начала рассматривали лишь как промежуточное решение и искались дальнейшие обоснования.

Во-вторых, даже если принять постулаты, теория Бора вместе с дополнением о собственном механическом моменте электрона не в состоянии удовлетворительно объяснить более сложные явления.

Несмотря на то, что удалось описать свойства и поведение атома водорода, введя поправки для значений механического и магнитного момента, причем поправки уже не могли быть выведены из принятой модели, эта теория оказалась абсолютно несостоятельной при описании атома гелия и давала неправильные значения энергий термов. Выводы, вытекающие из модельных представлений, в некоторых случаях должны были

быть скорректированы идентичным образом — вместо n' всюду вводилось l D n' 1, p

вместо l — значение l.l C 1/, однако в других случаях никакая корректировка не помогла. Поэтому в отличие от теории Бора ожидалось, что новая современная теория должна дать более естественное и наглядное или более общее обоснование квантования. Выбор орбит должен быть введен логически, а не основываясь на особых предположениях. Теория должна также охватывать те явления, с которыми теория Бора не справилась, такими, как, например, расчет атома гелия.

6Специально для этого случая.

110

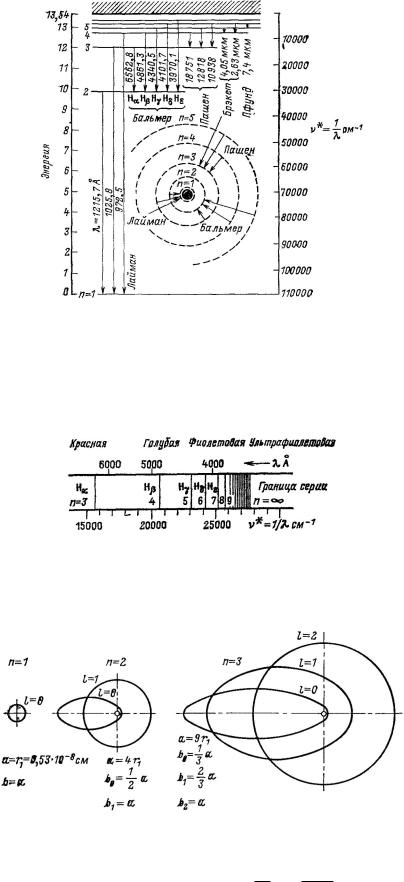
Рис. 78. Термы и спектральные линии атома водорода. Для каждой спектральной серии начальные состояния различны, а конечное — одно и то же. Так, серия Лаймана излучается, если электрон возвращается из различных возбужденных состояний в основное (n D 1). Серия Бальмера соответствует конечному состоянию n D 2 и т. д.

Рис. 80. Эллиптические орбиты атома водорода, характеризуемые квантовыми числами n и l . При одном и том же главном квантовом числе n большая ось и энергия разных орбит идентичны,

а малая ось может быть найдена из соотношения: b D a n' D a l C 1 : n n

111

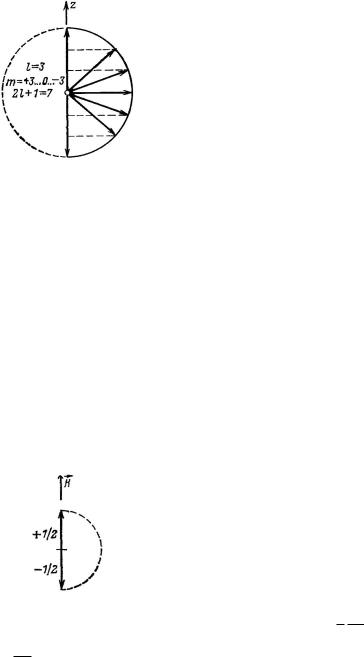
Рис. 81. Возможные ориентации орбитального момента.

1 h

Рис. 82. Две возможности ориентации момента количества движения электрона, равного 2 2 .

h

Разница ориентации дается величиной 2 .

112

13Уравнение Шредингера. Аналог волновой оптики. Интерпретация уравнения Шредингера.

13.1 Аналог волновой оптики

Идеи Шредингера, приведшие к волновой механике, теперь понимаются без труда. В предыдущей части было показано, что существует тесная связь между геомет-

рической оптикой и классической механикой: каждая из них может быть выведена из вариационного принципа, принципа Ферма и принципа Мопертюи. Путь луча света в среде с показателем преломления n определяется условием

ZP2

P1

а траектория электрона в поле с потенциалом U условием

Здесь Wp выражает потенциальную энергию, a qe подставляется с учетом знака. Известно, что геометрическая оптика является приближением волновой оптики, справедливым для длин волн , малых по сравнению с габаритами исследуемых объектов. Если размеры объектов малы, то для расчетов необходимо использовать точное волновое уравнение. Оно записывается в форме

где 4' — оператор Лапласа в декартовых координатах:

4' D @2' C @2' C @2' : @x2 @y2 @z2

В записанном здесь волновом уравнении ' может означать какую-либо компоненту электрической или магнитной напряженности электромагнитного поля световой волны. Если ' зависит лишь от одной координаты, например от x, то волновое уравнение упрощается и принимает вид:

Путем подстановки можно показать, что этому уравнению удовлетворяет волна вида

распространяющаяся в положительном направлении оси x со скоростью c при любом значении !.

Если ограничиться исследованием гармонических величин, т.е. величин, изменяющихся синусоидально в зависимости от времени, то возможно дальнейшее упрощение волнового уравнения. В случае

'.x; y; z; t / D '.x; y; z/e j 2 t

113

где множитель e j 2 t сокращается, так что ' зависит только от координат. Если учесть, что c= D , то не зависящее от времени волновое уравнение перепишется в виде

Попытаемся найти механический аналог этого уравнения. Колебания электрона тоже описываются волновым уравнением. Пусть состояние электрона описывается функцией

.x; y; z/e j 2 t , изменяющейся во времени-по гармоническому закону, а в пространстве — по закону, который будет определен позже, и пусть эта функция удовлетворяет волновому уравнению. Соответствующее волновое уравнение получают, подставляя в выражение (124) величину D h=mv, определенную по формуле де Бройля.

С другой стороны, известно, что значение v можно рассчитать исходя из равенства

Это и есть основное уравнение волновой механики — стационарное уравнение Шре-

функцией координат, то решение, включающее зависимость от времени, получают путем умножения на e j 2 t , где определяется из соотношения

W D h :

Окончательное решение, следовательно, будет иметь вид:

2

Необходимо подчеркнуть, что путь, приведший нас к уравнению Шредингера, не следует рассматривать как логический вывод. Напротив, уравнение Шредингера должно быть признано основным законом, к которому не приводят никакие предпосылки.

114

13.2 Интерпретация уравнения Шредингера

Исследуя значение уравнения Шредингера, отметим, прежде всего, что не следует задаваться вопросом о том, какой физический смысл может быть приписан величине

. Если эта величина имеет какое-то физическое значение, то ей можно приписать и определенные общие математические свойства: например, то что она ограничена на конечном интервале и исчезает на бесконечности. Физикам и особенно математикам давно уже известно, что если заданы определенные граничные условия, то уравнение типа волнового уравнения в оптике или уравнения Шредингера могут быть решены лишь при определенных значениях входящих в них констант. Достаточно вспомнить закрепленную на концах струну, мембрану или полый электрический резонатор, для которых решение возможно лишь тогда, когда существует вполне определенная связь между константой (содержащейся в волновом уравнении длиной волны) и геометрическими размерами, причем особую роль играют здесь целые числа. Шредингер показал, что в случае его волнового уравнения налагаемые на естественные условия также носят характер граничных условий, так что волновое уравнение в случае данной задачи имеет решение лишь при четко определенном наборе значений параметра W , т.е. полной энергии.

B наиболее интересных для нас случаях — это набор дискретных значений. Другими словами, микросистема, которая может быть рассчитана на основе уравнения Шредингера, обладает лишь дискретным набором значений энергий. В математике значения параметров, при которых существует решение, называют собственными значениями, а функции, удовлетворяющие уравнению при данных собственных значениях, — собственными функциями. После подстановки функции U.x; y; z/ в уравнение Шредингера физическая задача, сводится к задаче математической. Имеются значения

W1; W2; : : : ; Wn; : : :

полной энергии W , т.е. собственные значения, подлежащие определению, при которых уравнение Шредингера имеет решение. Решениями являются последовательность собственных функций

которые в данный момент имеют лишь второстепенную роль, так как в первую очередь нас будут интересовать разрешенные, т.е. возможные значения энергии.

Задача квантования, таким образом, превращается в математическую задачу определения собственных значений. Это положение метко выражено в заголовке статьи Шредингера, в которой приводится его знаменитое уравнение: «Квантование как задача о собственных значениях».

Величине можно теперь приписать следующее значение: зная природу световых фотонов, можно сказать, что величина '.x; y; z/, выражающая амплитуду световой волны, связана с вероятностью обнаружения в данной точке пространства большего или меньшего числа фотонов. На основании такого рассуждения можно утверждать, что и величина характеризует вероятность того, что электрон окажется в данной части пространства. Точнее, вероятность того, что электрон может быть встречен в элементарном объеме dV около любой выбранной точки, выражается в виде dV . Здесь — функция, комплексно-сопряженная функции . Это находится в полном согласии с тем фактом, что в случае света интенсивность (число фотонов) характеризуется квадратом

115

Достоверность того, что электрон должен находиться где-то в пространстве, выра-

при этом интегрирование должно проводиться по всему пространству.

Таким образом, нормировка позволяет определить любой постоянный множитель в -функции.

Так как квантование свелось к математической задаче, то понятно, что квантовая механика получает простейшие результаты, применяя относительно сложные математические методы.

В дальнейшем будут рассмотрены лишь те решения уравнения Шредингера, которые необходимы для понимания последующих рассуждений.

116

14 Полное уравнение Шредингера

Как было показано, решение стационарного (т.е. независящего от времени) уравнения Шрёдингера сводится к определению собственных значений, т.е. спектра уровней энергии En и соответствующих им собственных функций n. Волновая же функция

лишь процессы, протекающие строго монохроматически (т.е. с одной энергией). Наряду со стационарным существует также более общее, явно зависящее от време-

ни — полное, или нестационарное — уравнение Шрёдингера, позволяющее исследовать более широкий круг явлений.

Чтобы получить полное уравнение Шрёдингера, необходимо в стационарном уравнении исключить энергию E, играющую роль постоянного параметра. Представим для

Это уравнение имеет более общий характер и пригодно, в частности, для описания процессов, в которых потенциальная энергия U является функцией не только координат, но и времени. Если потенциальная энергия от времени не зависит, то нам достаточно решить стационарное уравнение Шрёдингера и определить все возможные собственные значения энергии En и принадлежащие им собственные функции n. Волновая функция, удовлетворяющая полному уравнению Шрёдингера, будет связана с этими частными решениями линейным соотношением:

X

.t / D Cne .i=~/En t n: n

В самом деле, подставляя это выражение в полное уравнение Шрёдингера и учитывая,

117

нетрудно убедиться, что .t / является общим решением полного уравнения Шрёдингера, так как

Случай монохроматической волны является частным случаем общего решения. Для этого надо положить Cj D 1 и Cn D 0 (если n ¤ j ).

Следует также заметить, что переход от стационарного уравнения к полному эквивалентен, в сущности, простой замене энергии E величиной i ~ @=@t , называемой в квантовой механике оператором энергии:

E D i ~@@t :

Действие этого оператора на какую-либо функцию сводится к обычному дифференцированию этой функции по времени, т.е. E является так называемым линейным дифференциальным оператором.

Для монохроматической волны, когда

.t / D e .i=~/En t n:

имеем

E .t / D En .t /:

Отсюда видно, что энергия Еn является собственным значением оператора энергии E. Кроме оператора энергии в квантовой механике есть и другие операторы, наиболее

важным из которых является оператор импульса:

который носит такое название потому, что его собственное значение для свободного движения совпадает с классическим импульсом. Например, действуя оператором p на волновую функцию свободной частицы, получаем:

где L — длина периодичности.

В данном случае собственным значением оператора p является классический импульс

p.

Пользуясь операторной символикой, полезной в том отношении, что она более наглядно иллюстрирует связь между квантовыми и классическими законами движения, уравнения Шрёдингера можно представить в виде

Таким образом, чтобы совершить формальный переход от классической теории к квантовой, следует в классическое выражение закона сохранения энергии

118

вместо энергии E и импульса p подставить соответствующие операторы и подействовать ими на волновую функцию.

Оператор p2=.2m0/ называют оператором кинетической энергии W, а WCU — оператором функции Гамильтона H, который ради краткости в дальнейшем мы будем называть просто гамильтонианом. Учитывая эти операторы, уравнение можно записать в виде

.E H/ .t / D 0:

В случае, когда потенциальная энергия U не зависит от времени, в силу соотношения

En.t / D En n.t /:

стационарное уравнение Шрёдингера приводится к форме

.En H / n.t / D 0:

Отсюда видно, что для стационарных процессов собственное значение гамильтониана равняется собственному значению энергии, точно так же, как и в классическом стационарном случае, функция Гамильтона равняется энергии частицы.

119

15 Уравнение Шредингера в операторной форме

До сих пор для решения любой квантовомеханической задачи мы использовали уравнение Шредингера

и подставляем в это уравнение потенциальную функцию Wp , соответствующую данной задаче. Именно так мы определяли собственные значения Wn и собственные функции

Здесь выражение, стоящее в скобках, рассматривается как оператор, который должен

Подобный оператор уже знаком нам: те же свойства наблюдаются при умножении вектора на тензор. Уравнение

O D W

H

можно очень просто пояснить. Представим на миг, что — это вектор, а O — тензор. При-

H

меним к вектору линейную операцию; результат представляет собой другой вектор. Особый интерес представляют векторы , которые после применения линейной операции становятся скалярами, кратными своему значению W . Такие -векторы называют собственными векторами, а значения соответствующих W — собственными значениями.

Решение уравнения Шредингера равнозначно определению собственных векторов и собственных значений линейного оператора.

Теперь следует обратиться к методу получения выражения (132). Запишем функцию Гамильтона механической системы, то есть сумму кинетической и потенциальной энергий, куда вместо скорости вводится на основании равенства v D p=m импульс

120