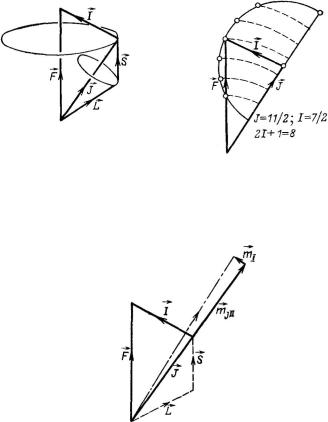
Магнитный момент атома получается как результат сложения суммарных магнитных орбитального и собственного моментов. Следует учитывать, что между полным спином и соответствующим ему магнитным моментом имеет место аномальное соотношение. В

данном случае векторы E и E прецессируют вокруг вектора полного момента E, как это

L S J

изображено на рис. 92. Вектор E сохраняет постоянное положение в пространстве, тогда

J

как векторы E и E могут и не сохранять постоянного значения, так как они влияют друг

L S

на друга вследствие взаимодействия магнитных моментов.

В соответствии с этим прецессирует и вектор суммарного магнитного момента mE J ,

23.4Влияние магнитного момента ядра на энергетические состояния атома

Магнитный момент имеет не только электрон, обращающийся вокруг ядра атома, но и само ядро, что связано с существованием у ядра момента количества движения (спина). Этот момент квантуется в соответствии с обычными правилами. Но так как масса нуклонов больше, то следует ожидать, что магнитный момент, связанный с моментом количества движения ядра соотношением

ml D 0 e hl; 4 m

окажется значительно меньше, а именно меньше во столько же раз, во сколько раз масса нуклона больше массы электрона. В связи с этим значение магнитного момента ядер выражают не в магнетонах Бора, а в единицах, называемых ядерными магнетонами:

Простая зависимость между магнитным моментом и механическим моментом E вида

I

в случае ядра не соблюдается. Этого не следовало и ожидать. Ведь и суммарный магнитный момент электронной подоболочки атома получился в виде

164

Рис. 95. Ввиду того, что магнитный момент ядра очень мал по сравнению с суммарным орбитальным магнитным моментом, разность энергий, соответствующих различным ориентациям, также очень мала.

Поскольку же ядро имеет сложную структуру, то и для него следует записать:

На рис. 94 показано, что полный механический, а следовательно, и полный магнитный момент атома получается как результат сложения орбитального, спинового и ядерного моментов. Магнитный момент ядра оказывает незначительное влияние на полный магнитный момент (рис. 95), так что и значения магнитной энергии, относящиеся ко всем возможным ориентациям,

лишь немного отличаются друг от друга. Расщепление уровней, проявляющееся затем в спектре, в соответствии со сказанным тоже очень незначительно. Поэтому вся возникающая в данном случае совокупность линий носит название сверхтонкой структуры.

165

где mF — магнитное квантовое число тонкой структуры, a gF — множитель Ланде, имеющий довольно сложное выражение.

В магнитном поле с большей напряженностью, но пока все еще остающимся слабым, E и

I

E уже не образуют одного суммарного вектора. Каждый независимо друг от друга квантуется в

J

поле E . Проекция определяется значениями магнитных квантовых чисел

H

для приращения энергии, обусловленного только магнитным моментом ядра, можно получить:

166

24Квантовая статистика. Понятие микросостояния в квантовой механике. Сопоставление классической статистики со статистикой Бозе—Эйнштейна и Ферми—Ди- рака. Состояние равновесия. Связь с макроскопической термодинамикой.

24.1Понятие микросостояния в квантовой механике

Вклассической статистике функция, описывающая распределение скоростей, находится в результате того, что пространство скоростей делят на ячейки и устанавливают, сколькими способами могут быть распределены отдельные частицы по отдельным ячейкам.

Между представлениями квантовой механики и классической статистики существуют значительные противоречия.

С позиций классической механики не имеет значения величина ячейки, требуется только, чтобы ячейка была достаточно маленькой (в макроскопическом отношении), чтобы можно было бы считать концентрацию частиц в ней постоянной величиной, и одновременно достаточно большой, чтобы было возможным само использование понятия концентрации (плотности) частиц.

Вквантовой механике распределение в ячейках уже потому не может быть совершенно произвольным, что если частица попадает в сосуд с объемом V , то ее место может быть обозначено с определенностью, обусловленной величиной этого объема. Следовательно, ее скорость, с точки зрения соотношения неопределенностей Гейзенберга, не может быть, разумеется, точно определена. Нет никакого смысла стремиться указать место частицы в пространстве скоростей с большей точностью, чем точность, определяемая, исходя из соотношения неопределенностей.

Другое существенное отличие постулатов квантовой механики заключается в том, что две одинаковые частицы принципиально неразличимы; следовательно, замена одной из таких частиц на другую такую же не приведет к новому состоянию. Подсчет числа микросостояний, благодаря которым реализуется данное макросостояние, в квантовой статистике осуществляется совершенно иначе, чем в классической статистике. Кроме того, должно быть учтено еще одно дополнительное требование: в соответствии с принципом Паули, если не рассматривается значение спинового квантового числа, в одном состоянии, определяемом тремя квантовыми числами, могут находиться максимум две частицы. Таким образом, в случае частиц, подчиняющихся принципу Паули, нельзя произвольным образом разместить сколь угодно большое количество таких частиц в одной ячейке.

Рассмотрим пространство скоростей и разделим его на столь маленькие ячейки, чтобы соотношение Гейзенберга выполнялось. Какой величины должны быть эти ячейки? Чтобы определить это, рассмотрим, прежде всего, систему пространственных координат x; y; z. Для простоты рассмотрим объем, ограниченный кубом с ребром a. Если центр куба лежит в центре системы координат, то неопределенность каждой пространственной координаты составляет a=2. Отсюда следует:

q D a D V 1=3 : 2 2

167

Выбираем, исходя из соотношения Гейзенберга, возможно меньшую неопределен-

ность

p q D h4 ;

чтобы получить простую формулу. Неопределенность скорости, таким образом, будет равна:

Длина ребра ячейки скоростей равняется, следовательно,

Между прочим следует заметить, что, если ячейки размещаются не в пространстве скоростей, а в пространстве импульсов, для выражения их величины получается простое выражение:

Это выражение еще больше упрощается, когда вводится понятие фазового пространства, элементарные ячейки которого имеют величину

Vf D V Vp D h3:

Величина элементарной ячейки, таким образом, равна h3, так как в фазовом пространстве пространственные координаты импульса задаются независимо друг от друга.

Результаты расчетов, помещенные в § 2-4, позволяют определить точное значениеVp . Из формулы ( ??) § 2-4 сразу следует, что

4 p2dp=.h3=V /

возможных решений относится к объему 4 p2dp пространства импульсов. Таким образом, можно фактически определить объем элементарной пространственной ячейки в фазовом пространстве как .h3=V /.

Итак, рассмотрим пространство скоростей, разделим его на ячейки в соответствии с вышесказанным и выделим сферическую оболочку толщиной vi . Энергию частиц, находящихся внутри подобной сферической оболочки, будем считать практически постоянной. Число ячеек в каждой сферической оболочке можно легко подсчитать: нужно только определить, сколько элементарных ячеек входит в сферическую оболочку. Число

На рис. 96 ячейки, находящиеся в каждой сферической оболочке vi , для упрощения рассмотрения расположим в виде столбцов друг за другом. Мы располагаем в каждом слое молекулы N1; N2; : : : ; Ni таким образом, чтобы выполнялись соотношения

X

i

168

Рис. 96. Ячейки пространства скоростей, находящиеся в сферической оболочке радиусом vi и толщиной vi .

X

i

С макроскопической точки зрения нас интересует, сколько молекул обладает в состоянии равновесия определенной энергией Wi . В конечном итоге нас интересует, какое из распределений N1; : : : ; Ni является наиболее вероятным.

24.2Сопоставление классической статистики со статистикой Бозе— Эйнштейна и Ферми—Дирака

Всоответствии с природой частиц можно выделить три случая.

1.Рассматриваются частицы, различающиеся между собой, и вычисляются все возможные варианты их расположения, которые образуют распределения N1; : : : ; Ni . Таким образом, возвращаемся к статистике Максвелла—Больцмана.

2.Частицы рассматриваются как принципиально неразличимые. Максимум вероятностей, подсчитанных таким образом, приводит к статистике Бозе-Эйнштейна.

3.Частицы рассматриваются как неразличающиеся и подчиняющиеся принципу Паули: в одной ячейке может быть не более двух частиц. Это допущение лежит в основе статистики Ферми—Дирака.

Как известно, N различающихся частиц могут быть распределены с помощью

N !

(310)

N1!N2! : : : Ni ! : : :

способов по любому числу оболочек таким образом, что в каждой из оболочек будет содержаться N1; N2; : : : ; Ni частиц. Теперь частицы, находящиеся на i -й оболочке, могут быть распределены по имеющимся там zi ячейкам Ni способами (образуя распределения из zi элементов в каждой из Ni оболочек, среди которых могут быть тождественные, отличающиеся лишь перестановкой частиц). Таким образом, получают:

169

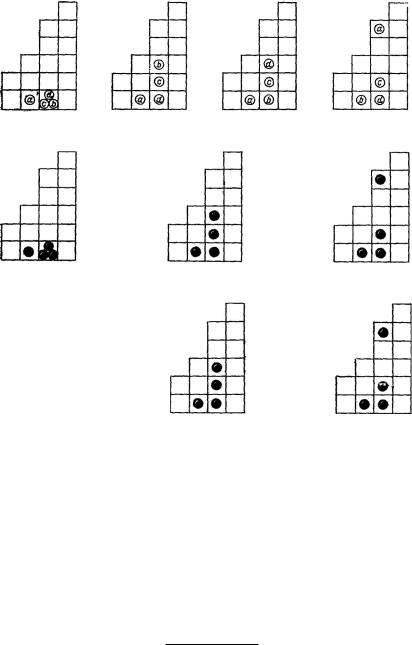
различных распределений, каждое из которых приводит к макроскопическому распределению N1; : : : ; Ni . Если определить максимум вышеупомянутой термодинамической функции вероятности, то придем к тем распределениям, которые характеризуют состояние равновесия в статистике Максвелла—Больцмана.

а)

б)

в)

Рис. 97. Некоторые микросостояния, реализующие микрораспределение Ni D 0; 1; 3; 0: а — в классической статистике; б — в статистике Бозе—Эйнштейна и в — в статистике Ферми—Дирака.

Для принципиально неразличимых частиц замена одной частицы другой физически не имеет смысла и не может привести к новому микросостоянию. Из всех вариантов распределений, имеющих место в случае заданных N1; : : : ; Ni , следует исключить все те, которые получаются вследствие обмена тождественными частицами, находящимися в различных оболочках. Таким образом, часть возможных состояний

Ni !

N1!N2! : : : Ni !

выпадает. Теперь вопрос состоит лишь в том, сколькими способами могут быть размещены Ni частиц в Zi ячейках, если эти частицы совершенно одинаковы.

На рис. 97 представлены некоторые вероятные варианты распределения 0; 1; 3; 0 : : :, соответствующие статистикам Максвелла—Больцмана, Бозе—Эйнштейна и Ферми—Ди- рака. Видно, что если частицы не могут быть индивидуализированы, т.е. если они неразличимы, два средних варианта будут идентичны. Последний вариант размещения отличается от обоих вышеупомянутых как в случае классической, так и в случае квантовых статистик.

170

Исследуем, прежде всего, сколькими способами могут быть размещены Ni частиц в Zi ячейках в случае, если частицы не только идентичны, но и подчиняются принципу Паули, так что в ячейку может попасть лишь один электрон. Ячейки пространства скоростей, в которых могут быть размещены два электрона с противоположно ориентированными спинами, представлены здесь как раздвоенные. На этот вопрос легко ответить. Расположим частицы рядом, как и пронумерованные ячейки на рис. 98. Если теперь мы отберем первые Ni ячейки из общего числа Zi ячеек и поместим в них по одной частице, то получим определенное распределение, при котором каждая из первых Ni ячеек содержит по одной частице, в то время как число частиц в остальных ячейках равно нулю. Рассмотрим все возможные способы размещений по Ni из общего числа Zi ячеек без повторений, т.е. найдем число сочетаний по Ni из Zi элементов:

Рис. 98. Пояснение к выводам функций распределения Бозе—Эйнштейна и Ферми—Дирака.

Число вариантов, с помощью которых можно реализовать распределение, характеризуемое N1; : : : ; Ni , составляет:

Если снять ограничение, обеспечивающее подчинение частиц принципу Паули, тогда в одной ячейке может находиться любое число частиц. Это означает, что для размещения Ni частиц согласно рис. 98 можно Ni раз использовать одну определенную ячейку. Тогда число вариантов размещения Ni частиц в Zi ячейках равно числу сочетаний по Ni из Zi элементов с повторением. Это число составит:

Число вариантов, реализующих распределение N1,. . . , Ni , таким образом, составит:

Значит, число вариантов, которые приводят к распределению N1; : : : ; Ni , по статистике Максвелла—Больцмана составляет:

171

Определим теперь вероятность различных распределений в несколько более общем виде. Предположим, что наше статистическое множество состоит из таких частиц, определенные энергетические состояния которых распределяются вдоль энергетической оси

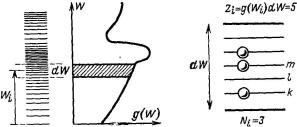
всоответствии с рис. 99. Возьмем энергетический интервал d W , достаточно малый с макроскопической точки зрения, но включающий много различных энергетических состояний. При различных значениях энергии W в энергетическую зону величиной d W будет попадать различное число энергетических уровней. Это число равно g.Wi /d W , причем функция распределения энергетических уровней g.W / учитывает вырожденные энергетические уровни с кратностью, соответствующей данному вырождению. Впрочем,

вэтом случае g.Wi /d W дает число ячеек, т.е.

Zi D g.Wi /d W:

Рис. 99. Роль единичных ячеек в общем случае играют допустимые энергетические уровни: а — функция g.W / задает число уровней Zi , приходящихся на единицу энергетического интервала; б — интервал dW в увеличенном виде. Ni частиц распределяются по уровням, обозначенным буквами k, l , m.

Нас интересует и распределение частиц по отдельным подсистемам в состоянии равновесия. Мы исходим из вполне приемлемого предположения, что любое из состояний всей системы, состоящей из N частиц, описанное с помощью функции , соответствующей данной полной энергии W0, — одинаково вероятно. Так, очевидно, осуществляется распределение N1; : : : ; Ni , к которому относится наибольшее число функций. Нам не остается ничего другого, как сосчитать все те различные -функции, которые относятся к данному распределению N1; : : : ; Ni , причем само собой разумеется, что нужно также учесть характер симметрии частиц. Для i -й подсистемы это должно дать, таким образом, Zi D g.W /d W возможных энергетических состояний и Ni распределенных по ним частиц. Если обозначить по порядку отдельные энергетические состояния буквами k, l , m (рис. 99), то соответствующая часть -функции, которая относится к частицам, находящимся в этой i -й подсистеме, равна:

Если рассматривать различающиеся частицы, то по k, l , . . . , r в совокупности Zi состояний могут быть распределены столько раз по 1, 2, . . . , Ni частиц, сколько может

172