25Газовые законы. Классический газ. Электронный газ. Фотонный газ.

25.1 Классический газ

Закон распределения скоростей Максвелла. Рассмотрим газ, заключенный в объем V , не подвергающийся воздействию внешних сил. Из статистики Максвелла—Больцмана мы знаем, что пространственное распределение концентрации газа равномерно, если число частиц, находящихся в i -й ячейке пространства скоростей, составляет:

Для определения концентрации частиц предположим, что объем ячеек составляет d 3, причем d так мало (и в принципе может быть безгранично уменьшено), что vi может рассматриваться как постоянное. Число молекул в объеме dvx , dvy , dvz , находящемся в точке vx , vy , vz , будет:

Отсюда следует, что функция распределения скоростей в пространстве скоростей может быть определена следующим образом:

Эта функция распределения представлена на рис. 100.

Интеграл от функции распределения по пространству скоростей должен давать общее число N частиц:

Z•C1

N D dN D .vx ; vy ; vz /dvx dvy dvz D

1

180

Наконец, функция распределения

Чаще всего нас интересует число тех молекул, абсолютная величина скорости которых находится в интервале между двумя граничными значениями, независимо от численных значений самих компонент. Мы хотим, таким образом, установить число тех точек, которые располагаются между сферическими оболочками с радиусом v и v C dv. Это легко подсчитать: в единичном объеме на расстоянии v от центра находится

молекул. Объем сферической оболочки, если ее толщина мала по сравнению с радиусом, равен произведению ее поверхности на толщину, т.е. 4 v2dv. Таким образом, число тех молекул, скорость которых лежит в интервале между v и v C dv, равно произведению этого объема на число молекул в единичном объеме, т.е.

Так приходят к выражению для основополагающего закона распределения скоростей Максвелла.

Теперь уже легко доказать, что выбрав ˇ равным 1= kT , мы поступили правильно. Подставим ˇ в функцию распределения Максвелла:

Величину кинетической энергии, приходящейся на одну частицу, т.е. W0=N , получают, принимая в указанном выше распределении среднюю величину энергии m2v2 :

181

В нашем случае при этом получим:

Как следует из определения температуры, средняя кинетическая энергия частиц с тремя степенями свободы составляет:

Определим число молекул с энергией, заключенной в интервале между W и W Cd W .

На рис. 100 представлен вид функции распределения.

Рассмотрим еще раз распределение скоростей Максвелла. Его существование может быть убедительно доказано с помощью качественных рассуждений.

Хотя плотность молекул вблизи центра максимальна, соответствующий объем сферической оболочки данной толщины мал, так что там обнаруживается лишь незначительное число молекул с небольшой скоростью. Несмотря на то, что при достаточно большом удалении от центра концентрация молекул уменьшается, за счет более быстрого увеличения объема сферической оболочки в ней будет обнаружено больше молекул с большей скоростью. Это увеличение продолжается до тех пор, пока все убыстряющееся уменьшение концентрации молекул в пространстве скоростей не скомпенсирует увеличение объема сферической оболочки. Затем функция распределения скоростей спадает, так что число молекул, обладающих большой скоростью, вновь уменьшится.

182

Рис. 100. Функции распределения для газообразного водорода в классической статистике.

Представить общий ход функций .vx ; vy ; vz / или .v/ и .W / помогают следующие соображения. Как известно, в случае гауссовой кривой, нормированной на единицу

константа обозначает рассеяние, равное квадратному корню из среднего арифметиче-

ского квадратов отношений от средней величины15. Величина рассеяния характеризует p

ширину кривой ошибок: при значении x D 2 значение функции соответствует 1=e максимального значения. Таким образом, если велико, то ход кривой достаточно полог, если же мало, то область, ограниченная кривой, очень узка, т.е. кривая имеет четко выраженный максимум в точке x D 0. То, что функция ошибок нормирована на единицу, означает, что суммарная площадь под кривой всегда равна принятой единице измерения. Это позволяет рассматривать отдельные значения кривой как величину соответствующей вероятности. В функции распределения

0 mv2

.vx ; vy ; vz / D A e 2kT

p

константа соответствует выражению kT =m. Среднее квадратичное отклонение, т.е. ширина графика, прямо пропорционально квадратному корню из значения температуры и обратно пропорционально квадратному корню из величины массы. Это означает, что кривая распределения скоростей в случае однородной смеси газов при высоких температурах приближается к прямой и лишь при малых температурах обнаруживает очень резкий максимум Причем при данной температуре более резко выраженным максимумом обладают те газы, молекулы которых имеют большую массу, в то время как кривая распределения скоростей в случае молекул с меньшей массой значительно более полога. Если теперь применить эти выводы к функции распределения

.v/ D Bv2 .vx ; vy ; vz /;

т.е. попытаться определить количество молекул (без учета их направления), скорости которых лежат в заданном интервале от v до v C dv, то придем к тем же результатам относительно величины среднего квадратичного отклонения. Ясно, что уменьшение концентрации превышает увеличение объема сферической оболочки только при весьма высоких значениях скоростей, когда среднее квадратичное отклонение кривой .vx ; vy ; vz /

15Обычно называют стандартным отклонением, средним квадратичным отклонением или средней квадратичной ошибкой. Гаусс называл ее просто средней ошибкой.

183

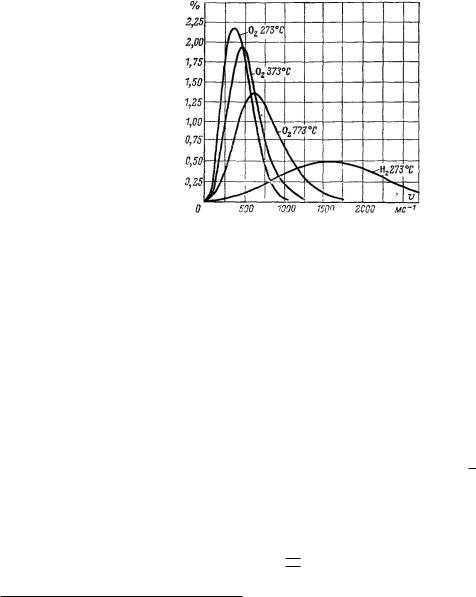
возрастает либо благодаря наличию высокой температуры, либо в связи с малой массой молекул газа. Это означает, что скорость, которой на данной кривой соответствует максимальная вероятность, сдвигается в направлении больших значений при одновременном возрастании среднего квадратичного отклонения. Все эти зависимости очень хорошо иллюстрирует рис. 101, где представлены распределения скоростей кислорода и водорода. Если мы выберем произвольную абсциссу, например 500 м/с, при различных температурах, то величина ординаты, соответствующей кислороду при 0˚C, составляет 1.75; это означает, что 1.75% всех молекул движется со скоростью от 495 до 505 м/с. Одновременно это означает, что вероятность обнаружения при наблюдении молекул, значение скоростей которых лежит в интервале между 495 и 505, составляет именно 1.75/100.

Рис. 101. Распределение скоростей молекул O2 и H2 при различных температурах. На этом рисунке единица интервала скорости равна 10 мс 1.

Очевидно, что при высоких температурах максимум функции распределения сдвигается в направлении больших значений скоростей и одновременно увеличивается стандартное отклонение значений скоростей. При этом кривая распределения расширяется. Средняя скорость молекул водорода оказывается выше в соответствии с молекулярной массой, которая у водорода меньше, чем у кислорода.

Исходя из функции распределения, могут быть определены различные характеристические значения скорости.

Прежде всего, следует упомянуть наиболее вероятную скорость. Под этим термином понимают значение скорости vm, соответствующее максимуму кривой распределения. Среднее значение функции распределения дает среднюю скорость v, также характеризующую движение молекул16. Напротив, температура связана с кинетической энергией таким образом, что определяющим является лишь среднее значение квадрата скорости, или корень из среднего значения квадрата скорости

q

v2 D v:Q

16Наиболее вероятная скорость представляет собой наиболее часто встречающееся значение скорости, т.е. скорость, присущую при данных условиях наибольшему числу молекул. Средняя скорость характеризует скорость молекул всего объема газа, т.е. она определяет среднюю кинетическую энергию молекулы газа при данных условиях. Эта характерная величина скорости может быть получена путем сложения всех скоростей, которыми обладают молекулы в рассматриваемом газовом объеме, и последующим делением суммы на общее число молекул. Поэтому среднюю скорость часто называют и средней арифметической скоростью.

184

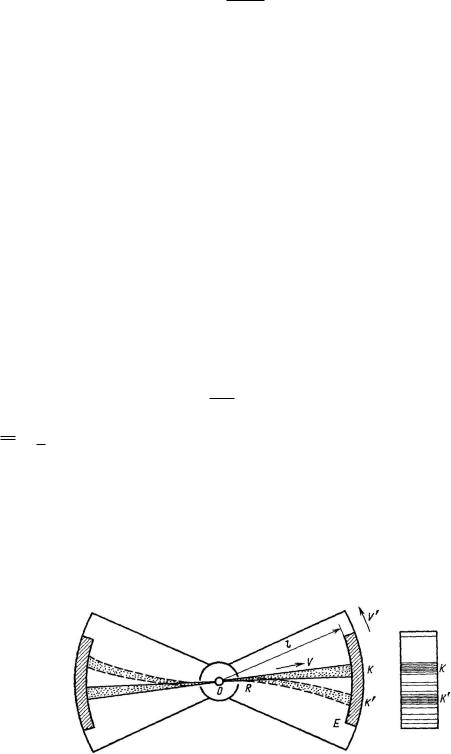
Для определения vm служит уравнение

d .v/ D 0:

dv

Наконец, выразим величину, определяющую среднюю энергию:

Отметим теперь следующую взаимосвязь между этими величинами:

p

т.е. v2 > v > vm.

Значения характерных для максвелловского распределения скоростей приведены на рис. 100.

В 1920 г. Штерн экспериментально доказал существование максвелловского распределения скоростей и одновременно измерил абсолютные значения скоростей молекул. Идея опыта заключается в следующем (рис. 102).

Рис. 102. Принципиальная схема устройства, служащего для экспериментального измерения скорости молекул. Молекулы, ударяющиеся об экран, характеризуются распределениями скоростей, приведенными справа.

185

Пусть известно, что шарик, направленный из точки O со скоростью v на экран E (причем экран неподвижен), ударится об экран в точке K. Шарик пройдет это расстояние за время l =v. Если теперь экран E будет двигаться со скоростью v0, то за время полета шарика l =v он пройдет путь

KK0 D vl v0:

Таким образом, шарик коснется экрана в точке K0. При выполнении измерений посеребренная платиновая проволока, находившаяся в вакуумированном объеме в точке, соответствующей точке O, раскалялась до очень высокой температуры. Атомы серебра испарялись с платиновой проволоки и разлетались равномерно по всем направлениям со скоростями, соответствующими распределению Максвелла. Ударяясь о холодную латунную пластину экрана E, они конденсировались на ней. Теперь начнем вращать всю установку. Атомы серебра, вылетевшие из точки O, больше не попадают в точку K, а в зависимости от их скорости окажутся в различных точках K0. При известных l и v0 соответствующая скорость легко может быть рассчитана, исходя из расстояния KK0, по уравнению KK0 D .l =v/v0. Зная толщину сконденсировавшегося слоя, можно сделать непосредственное заключение о функции распределения скоростей. Полученное экспериментальное значение средней скорости великолепно совпало с величиной, вычисленной теоретически. Однако значения, полученные при измерении толщины слоя, в связи с трудностями эксперимента соответствовали функции распределения скоростей Максвелла только качественно. Совершенного соответствия в этом случае и нельзя было бы ожидать, так как распределение скоростей атомов, испаряющихся с металлической поверхности, заведомо несколько отличается от распределения скоростей молекул газа, свободно перемещающихся в объеме.

Очевидно, еще более прямое доказательство существования максвелловского распределения скоростей можно обнаружить, изучая контуры спектральных линий, испускаемых возбужденными атомами газа. Предположим, что молекулы в состоянии покоя испускают световую волну определенной длины — 0. Предположим, что уже известен эффект Доплера, в соответствии с которым длины волн испускаемого света, если источник света удаляется от наблюдателя, соот-

ветствуют отношению v

D 0 1 C c ;

где v, как и раньше, есть скорость удаляющихся молекул, а c обозначает скорость света. При наблюдении за светом, излучаемым молекулами, скорости которых соответствуют максвелловской функции распределения скоростей, было обнаружено, что допускаемая длина волны не равна 0, а спектральная линия вследствие наличия молекул, обладающих различными скоростями, уширяется, так как испускаются длины волн, которые могут быть как больше, так и меньше 017. По измерению этого уширения можно сделать заключение о распределении скоростей. Результаты этих экспериментов достаточно хорошо согласуются с учетом погрешностей измерений с рассчитанными теоретически.

Давление газа. Используя приведенные выше рассуждения, можно легко вычислить давление газа. Молекулы движутся с большой скоростью и при этом очень часто ударяются о стенки сосуда. Эта беспрерывная бомбардировка оказывает силовое воздействие на стенки сосуда.

Рассмотрим молекулу (рис. 103), которая ударяется о стенку под углом # со скоростью v. В результате удара составляющая скорости v cos # , перпендикулярная стенке, меняет знак, так что изменение импульса частицы и одновременно импульса, передава-

17Это связано с тем, что знак добавки, обусловленной эффектом Доплера, связан с тем, удаляется или приближается источник света к наблюдателю. Ввиду того что вдоль луча зрения высвечиваются возбужденные молекулы, скорости которых направлены как к наблюдателю, так и от него, линии симметрично уширяются.

186

Из частиц, вектор скорости которых лежит в данном угловом диапазоне между # и # C d# , а модуль вектора скорости заключен в интервале v и v C dv, в единицу времени достигают стенки лишь частицы, находящиеся в объеме призмы с площадью основания 1 м2 и высотой v cos # . Частицы ударяются об основание этой призмы и передают ему импульс 2mv cos # . Число частиц, соударяющихся с единицей поверхности стенки в единицу времени, составляет, таким образом, n.v; # /dvd# v cos # . При этом концентрация молекул, вектор скорости которых лежит в угловом диапазоне d# , а модуль вектора скорости в диапазоне dv, обозначена n.v; # /.

Изменение импульса в единицу времени, отнесенное к единице поверхности, определяет соответствующее давление, так что давление, создаваемое рассматриваемыми частицами, составляет:

d 2p D n.v; # /dvd# cos # 2mv cos #:

Если распределение скоростей пространственно изотропно, то соответствующая часть всех частиц движется со скоростью, приходящейся на конус, с углом при вершине, заключенным между # и # C d# (рис. 104). Это число частиц равно площади 2 sin # d# круга, вырезанного образующей конуса из общей поверхности шара единичного радиуса, равной 4 :

187

далее

Такой же вывод можно получить с помощью значительно более простых предположений относительно движения молекул газа. Предположим, что 1/6 общего числа молекул движется в направлении положительной оси x, а 1/6 — в направлении отрицательной оси

x, кроме того, по 1/3 от числа молекул движется параллельно направлениям оси y и z, p

причем все движутся со средней квадратичной скоростью v v2. При этом движении молекулы не мешают друг другу, и каждая молекула передает стенке сосуда в данном случае импульс 2mv. Следовательно, полный импульс, переданный от v n=6 молекул, движущихся со средней скоростью v в единицу времени, т.е. давление, составляет:

что находится в полном соответствии с прежним результатом. Все это достойно упоминания, потому что в кинетической теории часто случается, что простейшие гипотезы приводят к тем же результатам, что и сложнейшие, и результаты, полученные двумя методами, различаются лишь коэффициентами, мало отличающимися от единицы. Кроме того, надежность результатов сложных решений часто бывает спорной, так как здесь для окончательных выводов часто используются недостаточно обоснованные гипотезы.

Уравнение состояния газа. Если объем газа V содержит N молекул, то

n D NV ; p D m3 NV v2:

Таким образом, давление обратно пропорционально объему. При равной кинетической энергии газ, занимающий половинный объем, оказывает двойное давление, вследствие большей концентрации молекул, ударяющихся о стенку в единицу времени. Если перенести V в левую часть вышеприведенного уравнения, то получим соотношение:

где V теперь означает объем одного кмоля газа, a N0 — число находящихся в нем молекул; тогда для этого газа имеем:

В соответствии с макроскопическими измерениями термодинамика дает:

т.е. произведение давления газа на занимаемый им объем прямо пропорционально абсолютной температуре. Величина коэффициента пропорциональности R, так называемой

188

газовой постоянной, в случае одного кмоля газа (а приведенные рассуждения относятся как раз к этому количеству газа) равна:

При сравнении уравнений (383) и (384) видно, что они идентичны при условии, что

Отсюда внутренняя энергия 1 кмоля газа составляет

Исходя из этого выражения, легко вычислить удельную теплоемкость газа при постоянном объеме. Эта величина, по определению, равна количеству подводимого тепла (поскольку объем газа остается постоянным, то никакая внешняя работа не совершается), необходимого для повышения температуры на один градус. В данном случае при количестве газа, равного 1 кмолю, это составит:

Чтобы определить удельную теплоемкость газа при постоянном давлении, прежде всего надо определить, какую работу совершает газ, когда он расширяется при постоянном давлении. Чтобы повысить температуру газа на один градус при постоянном давлении, необходимо большее количество тепла, так как оно должно, с одной стороны, увеличить внутреннюю энергию газа, а с другой — совершить внешнюю работу. Разность количеств тепла, которые необходимо подвести для нагрева газа на 1˚C при постоянном давлении и постоянном объеме, будет равна как раз этой работе.

При перемещении поршня в цилиндре при постоянном давлении на расстояние d l совершенная работа будет равна d W D pAd l D pdV .

Из уравнения состояния одновременно вытекает, что при постоянном давлении pdV D Rd T , так что для повышения температуры на 1˚С требуется работа, равная R. Следовательно, в данном

Отсюда отношение удельных теплоемкостей идеального газа при постоянном давлении и

постоянном объеме составит:

cp D 5 D ; cv 3

что, таким образом, точно соответствует значению, измеренному в случае одноатомного газа при комнатной температуре. Для многоатомных газов и при значительных изменениях температуры эта зависимость изменится. Если вспомнить рассуждения, которые привели нас к соотношению

W D 32 kT;

то мы увидим, что число 3 появилось из допущения перемещения молекул независимо друг от друга в направлениях, параллельных трем осям координат. В случае движения молекул в плоскости средняя кинетическая энергия составила бы .2=2/kT . Если частица может осуществить f различных независимых перемещений, другими словами, если число ее степеней свободы равно

189

f , то ее кинетическая энергия составит .f =2/kT 18. В соответствии с этим величина удельной теплоемкости меняется и составит:

и

D cp D f C 2 : cv f

Теперь мы можем, наконец, определить скорость молекулы в численном выражении, а именно с помощью определенной ранее макроскопической оценки.

Соответствующее соотношение имеет вид:

v2 D 3 kT D 2RT I m N0m

при этом N0 обозначает число молекул в 1 кмоле газа, а m — массу частицы. Произведение N0m, таким образом, равно массе M всего газа в 1 кмоле. Отсюда

qr

где под vQ подразумевается квадратный корень из среднего значения квадрата скорости. Теперь уже известны все данные для численной макроскопической оценки. Для водорода при 0˚С температура E D 273 К, M D 2, т.е.

Таким образом, молекулы водорода движутся со скоростью почти два километра в секунду. Молекулы газов с большой массой соответственно выше приведенному соотношению перемещаются медленнее, пропорционально корню квадратному из молекулярной массы.

Таблица 3. Средняя скорость молекул некоторых газов при 273 К.

В табл. 3 приведены значения средних скоростей молекул некоторых газов. Правдоподобие такой оценки скоростей подтверждает то соображение, что звук как чередование сжатия и разрежения воздуха, молекулы которого перемещаются в результате соударений, — распространяется примерно с такой же скоростью. В дальнейшем мы увидим, что приведенное выше значение может быть подтверждено прямым опытом.

Длина свободного пробега, диаметр молекулы. Теперь определим, какой путь в среднем проходит молекула до соударения с другой молекулой. Отсюда можно вычислить также число соударений в секунду и диаметр молекулы. Предположим, что выбранная молекула движется среди других, неподвижных. Вопрос: какова вероятность того, что молекула на коротком отрезке dx столкнется с любой другой молекулой газа? Рассматриваемая молекула диаметром 2r0 столкнется с другой молекулой того же диаметра в

18Это является прямым следствием закона равномерного распределения энергии по степеням свободы.

190

том случае, если она пройдет на расстоянии 2r0 от центра второй молекулы (рис. 105). Эта задача эквивалентна столкновению точки (центра молекулы) с другой молекулой диаметром 4r . B соответствии с предложенным Борном сравнением этот случай аналогичен слепому полету пули между деревьями в лесу. Вероятность попадания пули в какое-нибудь дерево, находящееся на определенной глубине в лесу, равна отношению общей площади деревьев, видимых нами в пределах заданной глубины, к общей поверхности рассматриваемой цели. Наша молекула пролетает через площадку размером в 1 м2 (рис. 106). В 1 м3 может находиться n1 молекул, следовательно, на глубине dx встречается n1dx молекул, а их общая площадь равна n1 .2r0/2dx. Так как вся рассматриваемая площадь равна 1 м2, то это выражение и представляет собой искомую вероятность.

Предположим теперь, что площадь в 1 м2 пересекается молекулярным пучком, состоящим из n2 молекул. На основе вышеизложенного n2n1 .2r0/2dx молекул сталкивается на отрезке dx и в дальнейшем выбывает из пучка вследствие рассеяния. Если уменьшение числа молекул, находящихся в пучке, обозначить через d n2, то получим:

d n2 D n2n1 .2r0/2dx

и число молекул, оставшихся в пучке, после интегрирования вышеуказанного уравнения окажется равным:

Таким образом, число молекул экспоненциально уменьшается с ростом длины пробега. Некоторые молекулы вследствие соударения выбывают из пучка уже вначале, в то время как другие не претерпевают столкновений, пробегая очень большие расстояния. Можно вычислить среднюю длину пробега молекулы без соударений. На основе вышеприведенной формулы можно определить число тех молекул, которые соударяются на длине пробега x. Таким образом, для них можно получить выражение средней величины свободного пробега:

Как и можно было ожидать, эта величина обратно пропорциональна концентрации

191

газа и диаметру молекулы. Известно, что средняя скорость

qr

Это путь, который проходит молекула в секунду. Так называемое число соударений, показывающее, как часто одна молекула соударяется с другими молекулами за секунду,

При точном вычислении следует учесть тот факт, что молекулярный пучок движется не среди неподвижных, а среди перемещающихся молекул, распределение скоростей которых является максвелловским. При рассмотрении соударений в данном случае учитывают только относительную скорость. Однако общие выводы от этого практически не зависят, и в результате получим:

Функция распределения относительных скоростей определяется исходя из того факта, что «относительная» энергия равна:

Данное выражение получено из предположения равенства масс молекул. Функция распределения, таким образом, имеет вид:

Однако рассматриваемая молекула претерпевает за секунду

столкновений, где означает эффективное сечение. Отсюда может быть получено значение интеграла из уравнения (375), которое равно:

192

Теперь мы можем также получить число всех соударений в единицу времени в единице

объема:

z n

zобщ D 2 ;

так как каждое столкновение подсчитано дважды.

Средняя длина свободного пробега может быть определена на основании макроскопических измерений. Пусть газ пронизывает упомянутый молекулярный пучок, состоящий из параллельно движущихся молекул. Если мы измерим уменьшение его интенсивности в двух различных точках, то из двух полученных результатов измерений можно определить (по уравнению (388)) 1=n .2r0/2, т.е. длину свободного пробега .

Зная длину свободного пробега, можно определить диаметр молекул газа, если известно число молекул в 1 м3 газа при нормальном давлении. Из уравнения (389) следует:

Зная число Авогадро, можно подсчитать среднее расстояние t между молекулами. Для этого используют соотношение

t 3N0 D 22:4 м3:

В выражении длины свободного пробега встречается произведение n.2r0/2. Следовательно, 2r0 может быть вычислено только (при условии, что уже определена экспериментально), если известно n. Эту величину до сих пор мы заимствовали из другой области физики. Однако если измерить объем сжиженного газа, который при нормальных условиях занимает 1 м3, то получим полный объем, занимаемый молекулами. Это составит

4 .r0/3n :

3

В этом состоянии молекулы плотно прижаты одна к другой. Благодаря этому измерению можно определить nr03, а измерив , установить значение n.2r0/2: из двух измерений можно независимо определить как n, так и r0. Если известно n, то, следовательно, известно число Авогадро N0.

Рис. 107. Обычный газообразный водород при увеличении в несколько миллионов раз. Длина свободного пробега D 1:2 10 5 см. В принятом масштабе это соответствует примерно длине диагонали страницы.

Таким образом, исходя из макроскопических измерений, можно определить все микроскопические характеристики: радиус молекулы r0, число молекул в кубическом метре n, их массу m, скорость v, среднюю длину свободного пробега , и т.д.

Эти параметры представлены на рис. 107 на примере небольшого количества водорода в нормальном состоянии при увеличении в несколько миллионов раз. Сторона

193

ребра сосуда в 1 см достигает при таком увеличении примерно 30–40 км. Эту длину, т.е. расстояние, соответствующее после увеличения 30–40 км, а на самом деле 1 см, молекула пробегает со скоростью соответственно увеличенной примерно 200 000 раз в секунду. Отсюда становится понятной столь значительная частота соударений различных молекул.

Весьма интересно исследовать поведение газа при изменении некоторых внешних условий. Изменение температуры или атомной массы оказывает весьма слабое влияние на длину свободного пробега или число соударений, так как, во-первых, эти величины экспериментально могут быть изменены только в сравнительно узких пределах, а к тому же в формулу они входят под знаком корня. При повышении температуры от 0 до 100 000˚C число соударений изменится лишь на два порядка, а длина свободного пробега в случае идеального газа совсем не изменяется. Наоборот, давление газа и его плотность могут быть практически изменены на десять порядков. Можно представить, с одной стороны, атмосферное давление, а с другой — вакуумные лампы, давление в которых достигает 10 8 торр. В таблице 4 представлены значения длины свободного пробега и числа соударений при температуре 273 К и давлении 1 торр. Важно, что длина свободного пробега при низких давлениях соизмерима с размерами сосудов, используемых для опытов.

Таблица 4. Длина свободного пробега и число соударений различных молекул газа при 273 К и p D 1 торр

Этот факт играет очень важную роль в объяснении явлений, сопутствующих исследованиям прохождения газа через щель или трубку, теплопроводности и внутреннего трения газа при низких давлениях, т.е. при условиях, сильно отличающихся от нормальных.

Отклонение от уравнения состояния идеального газа. Уравнение Ван-дер-Ваальса. Уравне-

ние

устанавливает зависимость между макроскопическими характеристиками идеального газа. Этот газ характеризуется тем, что его молекулы, рассматриваемые обычно как точечные, представляют собой упругие шары, которые при непосредственном контакте не оказывают друг на друга никакого воздействия. В реальных газах иначе: молекулы имеют конечный диаметр и при непосредственном контакте притягивают друг друга. Вследствие этого уравнение состояния реального газа отличается от уравнения состояния идеального газа.

Прежде всего, исследуем отличия от состояния идеального газа, обусловленные конечным объемом молекул. Легко видеть, что в данном случае давление увеличивается, потому что центр молекулы, когда она ударяется о стенку, не может приблизиться к стенке больше чем на расстояние r0. Этот эффект станет еще ощутимее, если принять во внимание соударение молекул друг с другом. Если представить себе «лобовое» соударение двух молекул, при котором они обмениваются импульсами, то центры этих молекул могут сблизиться лишь на расстояние 2r0 и, следовательно, можно сказать, что импульс одной участвовавшей в этом соударении молекулы «перепрыгивает» через расстояние r0 и таким образом передается дальше другой молекуле. Можно видеть, что в реальном газе молекулы соударяются друг с другом чаще, а именно в

194