
- •1. Уравнения движения воды и наносов
- •2. Дискретизация уравнений.
- •3. Применение метода характеристик к
- •4. Метод конечных разностей
- •5. Метод конечных элементов
- •5.4. Одновременная аппроксимация дифференциальных уравнений и краевых условий
- •5.5. Кусочно-определенные базисные функции и метод конечных элементов
- •6. Калибровка модели
Условные обозначения
А - постоянная интегрирования
а - параметр базисной функции
В - ширина потока по зеркалу воды
b - поперечная координата в планах течений
С - коэффициент Шези
с
=![]() - волновая скорость
- волновая скорость![]()
D - коэффициент в формуле расхода наносов
d - диаметр частиц грунта
Е - число элементов, составляющих двумерную область
е - элемент двумерной области
f - функция
G - функция
g - ускорение свободного падения
Н - средняя глубина потока
h - глубина вертикали
I - уклон свободной поверхности
Io - уклон дна
If
=![]() - уклон трения
- уклон трения
i - порядковый номер поперечного сечения
k - порядковый номер момента времени; коэффициент
L - длина потока
М
=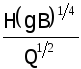 - инвариант
естественного квазаравномерного потока;
N
- число сечений
или участков
- инвариант
естественного квазаравномерного потока;
N
- число сечений
или участков
m - порядковый номер функции
N - базисная функция
n - коэффициент шероховатости
Q - расход воды
Qs - твердый расход
q - удельный расход
R - невязка
r - местный радиус линии тока
r* - местный радиус поперечника
p - функция
t - время
U - средняя на вертикали или в поперечном сечении продольная скорость течения
V - средняя на вертикали поперечная скорость
![]() -
динамическая скорость
-
динамическая скорость
![]()
![]() -
критическое значение динамической
скорости на зернистом дне
-
критическое значение динамической
скорости на зернистом дне
W
=![]() - результирующая скорость в плановой
задаче
- результирующая скорость в плановой
задаче
Wi - весовая функция
Zo - высота дна
![]() -
весовой коэффициент в разностной схеме
-
весовой коэффициент в разностной схеме
![]() -
коэффициент потерь энергии при расширении
потока
-
коэффициент потерь энергии при расширении
потока
Г - граница области
![]() -
дельта-функция Дирака
-
дельта-функция Дирака
![]() -
коэффициент пористости
-
коэффициент пористости
![]() -
константа Кармана
-
константа Кармана
![]() -
кинематический коэффициент вязкости
-
кинематический коэффициент вязкости
![]() -
плотность жидкости
-
плотность жидкости
![]() -
плотность твердых частиц
-
плотность твердых частиц
![]() -
касательное напряжение на дне
-
касательное напряжение на дне
![]() -
аппроксимируемая функция
-
аппроксимируемая функция
![]() -
аппроксимирующая функция
-
аппроксимирующая функция
![]() -
функция, определяемая краевыми условиями
-
функция, определяемая краевыми условиями
![]() -
двумерная область
-
двумерная область
![]() -
площадь поперечного сечения потока
-
площадь поперечного сечения потока
1. Уравнения движения воды и наносов
в естественных руслах
Для такого движения характерны: большие числа Рейнольдса, изменения плотности вещества лишь при фазовых переходах, сложная геометрия русел и способность потоков изменять свои русла.
Достаточно изучено лишь так называемое плавно изменяющееся движение воды, удовлетворяющее условиям малой кривизны и малой расходимости линий тока. Первое из этих условий позволяет пренебрегать влиянием центростремительных ускорений, второе условие разрешает считать, что все сопротивление движению обусловлено внешними силами - трением на твердых стенках. Оговоримся лишь, что это трение есть трение между движущейся жидкостью и ее молекулами, прилипшими к твердым стенкам.
Одномерное плавно изменяющееся движение описывается системой уравнений Сен Венана:
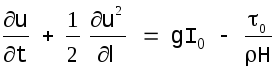 (1.1)
(1.1)
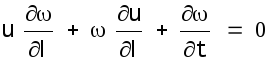 (1.2)
(1.2)
Уравнение (1.1) выражает закон изменения количества движения. Его члены отнесены к единице массы жидкости. Ось l- плоская кривая с большими радиусами кривизны. Левая часть уравнения содержит ускорения, испытываемые жидкостью, правая часть - силы тяжести и трения. Все скорости в поперечном сечении считаются одинаковыми. Уравнение (1.2) есть уравнение неразрывности. В общем случае такое уравнение выражает закон сохранения массы жидкости. В случае несжимаемой жидкости оно вырождается в закон сохранения ее объема. Касательные напряжения на дне и стенках русла принято определять по формуле Шези:
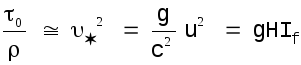
![]() (1.3)
(1.3)
Уравнения двумерного (планового) плавно изменяющегося движения в системе прямоугольных декартовых координат имеют вид:
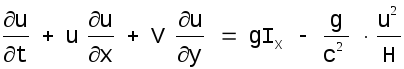 (1.4)
(1.4)
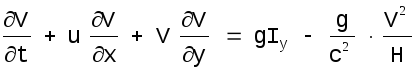 (1.5)
(1.5)
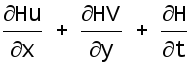 = 0
(1.6)
= 0
(1.6)
Вошедшие в уравнения(1.4) и (1.5) выражения сил трения имеют смысл только в том случае, если коэффициент Шези не зависит от направления движения. Этому условию удовлетворяют (наряду с некоторыми другими) следующие формулы:
Маннинга
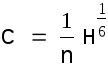 (1.7)
(1.7)
Штриклера
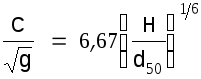 (1.8)
(1.8)
Зегжды
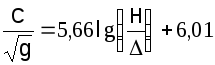 (1.9)
(1.9)
Графа
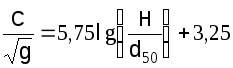 (1.10)
(1.10)
Лимериноса
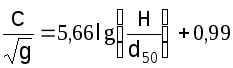
![]() (1.11)
(1.11)
Различие результатов у авторов последних трех формул обусловлено различными условиями гидравлического моделирования, в которых эти зависимости были получены. Так, донные частицы в опытах Зегжды состояли из песка и мелкого гравия и были приклеены к дну лотка; в опытах Графа использовались частицы гальки, лежавшие свободно; измерения Лимериноса были сделаны в малых реках с галечным дном (без гряд).
Донные гряды имеют определенную ориентацию - их гребни нормальны векторам придонных скоростей. Направление осей x, y может не согласоваться с этой ориентацией. Поэтому применять формулы сопротивления, построенные для грядового дна в уравнениях (1.4) и (1.5), нельзя. Строго говоря, и поверхность безгрядового галечного дна не изотропна. У лежащих на дне частиц гальки длинная ось обычно направлена по потоку. Поэтому сопротивление движению воды вдоль и поперек галечного русла не одинаковое.
Переходя к не плавно изменяющемуся движению, следует вспомнить о трех его особенностях. Первая из них - это появление добавочных сил трения при расширении потока. Вторая - влияние изгиба русла на его гидравлическое сопротивление. Третья - существование сил трения между смежными плановыми струями двумерных потоков. Сразу же можно заметить, что влияние изгиба на сопротивление естественных русел не велико. Эксперименты и натурные наблюдения показывают, что основная доля сопротивления в изогнутом русле обусловлена влиянием побочня, который формируется у выпуклого берега. В цилиндрическом русле сам факт изгиба не вызывает заметных потерь энергии (если, конечно, поток не отрывается от берегов). А.Я.Милович объяснял это тем, что плановое движение жидкости при безотрывном изгибе является безвихревым. Он демонстрировал это, пуская в поток пробку с начерченным на ней крестиком. Двигаясь по криволинейной траектории, пробка не поворачивалась - крестик не изменял своей ориентировки. Обращаясь к натурным данным, полезно вспомнить также, что в интенсивно меандрирующем русле среднего Иртыша потери энергии очень малы - они составляют в межень лишь 2-3 см/км.
Таким образом, остаются два обстоятельства: потери энергии при расширении потока и трение между плановыми струями в двумерном движении. Оба эти явления вызываются внутренними силами и, следовательно, им нет места в уравнении количества движения. Уравнения не плавно изменяющегося движения должны записываться в форме уравнений сохранения энергии. В одномерном случае необходимо учитывать лишь потери на расширение, и уравнение движения принимает вид:
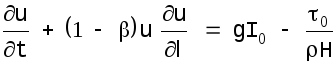 (1.12)
(1.12)
Оно
отличается от уравнения Сен Венана не
только множителем перед конвективным
членом, но и смыслом остальных, внешне
идентичных, членов. Конвективный член
в уравнении (1.12) выражает не ускорение
единицы массы жидкости, а быстроту
изменения вдоль потока кинетической
энергии этой массы. Член с трением
выражает не силу трения на дне потока,
а интенсивность потерь энергии,
обусловленных этой силой. Коэффициент
![]() ,
по мысли Буссинеска, выражает
неравномерность распределения скоростей
в поперечном сечении и добавочные потери
энергии, вызванные расширением. Когда
стенки потока расходятся, в нем усиливается
турбулентное перемешивание жидкости,
а это ведет к увеличению потерь энергии.
К сожалению, количественная сторона
этого явления изучена недостаточно. В
расчетах обычно принимают, при безотрывном
расширении
,
по мысли Буссинеска, выражает
неравномерность распределения скоростей
в поперечном сечении и добавочные потери
энергии, вызванные расширением. Когда
стенки потока расходятся, в нем усиливается
турбулентное перемешивание жидкости,
а это ведет к увеличению потерь энергии.
К сожалению, количественная сторона
этого явления изучена недостаточно. В
расчетах обычно принимают, при безотрывном
расширении
![]()
![]() ;
и при расширении с отрывом потока от
дна или берегов
;
и при расширении с отрывом потока от
дна или берегов
![]() .
При
.
При
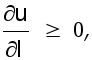 коэффициент
коэффициент
![]() .
.
Криволинейной
оси потока
![]() ,
при переходе к двумерному движению,
должна отвечать система криволинейных
плановых координат
,
при переходе к двумерному движению,
должна отвечать система криволинейных
плановых координат
![]() .
Наиболее общей и единственно строгой
из таких систем является система
натуральных координат, в которой
координатными линиями служат линии
тока. В каждой точке плана течений
имеется свой координатный базис (рис.1).
Уравнения не плавно изменяющегося
двумерного (планового) движения и
отвечающее им уравнение неразрывности
в натуральных координатах имеют вид:
.
Наиболее общей и единственно строгой
из таких систем является система
натуральных координат, в которой
координатными линиями служат линии
тока. В каждой точке плана течений
имеется свой координатный базис (рис.1).
Уравнения не плавно изменяющегося
двумерного (планового) движения и
отвечающее им уравнение неразрывности
в натуральных координатах имеют вид:
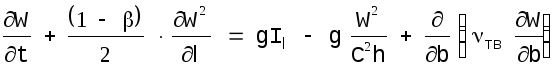 (1.13)
(1.13)
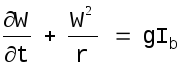 (1.14)
(1.14)
![]()
 (1.15)
(1.15)
Здесь r обозначает радиус кривизны линии тока, а r* - радиус кривизны поперечника. В уравнении движения (1.13) учтены как потери энергии при расширении потока, так и потери, обусловленные трением между плановыми струями. Интенсивность этих потерь выражается последним членом правой части уравнения. Ф. Энгелунд, использовав упрощающее представление о скалярном коэффициенте турбулентной вязкости, проинтегрировал известный параболический закон изменения этого коэффициента по вертикали и получил формулу:
![]() (1.16)
(1.16)
Турбулентная
вязкость выравнивает распределение по
ширине потока скоростей течения и
коэффициентов трения. Основываясь на
этом и выполнив расчеты, Б.М. Николаев
предложил отбросить последний член
уравнения (1.13) и в виде компенсации за
это считать коэффициент Шези постоянным
поперек потока. В этом случае в формулу
Маннинга можно подставить не местную,
а среднюю глубину
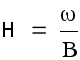 .
Для рек с большими значениями отношения
ширины к глубине предложение Николаева
оправдано.
.
Для рек с большими значениями отношения
ширины к глубине предложение Николаева
оправдано.
Планы течений строят для установившегося движения. Положив локальное ускорение равным нулю, будем иметь вместо (1.13) уравнение
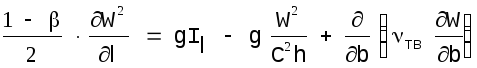 (1.17)
(1.17)
В плесовых лощинах можно пренебрегать как эффектами расширения, так и трением между струями, т.е. допустимо считать движение плавно изменяющимся. В этом случае получим:
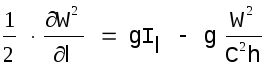 (1.18)
(1.18)
Основоположник плановой гидравлики Н.М. Бернадский пользовался уравнением движения в этом виде. Если ввести в выражение потерь энергии формулу Маннинга, получим:
![]()
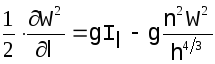 (1.19)
(1.19)
В
равномерном потоке, т.е. при
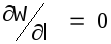 , считая, что уклон
, считая, что уклон
![]() и коэффициент шероховатости n не
меняются поперек потока, найдем, что
удельный расход пропорционален глубине
вертикали в степени 5/3. Если принять
предложение Николаева, получим, что
удельный расход пропорционален глубине
в степени 3/2.
и коэффициент шероховатости n не
меняются поперек потока, найдем, что
удельный расход пропорционален глубине
вертикали в степени 5/3. Если принять
предложение Николаева, получим, что
удельный расход пропорционален глубине
в степени 3/2.
В
сопротивлении русел, сложенных частицами
песка, главную роль играет не сопротивление
зернистой шероховатости, а сопротивление
донных гряд - так называемая
макрошероховатость дна. Для частиц
среднего и мелкого песка, т.е. в диапазоне
крупностей 0,5
![]() 0,1
мм,различия диаметров частиц не
существенны и в расчетные выражения
входят лишь элементы потока. Укажем две
формулы этого рода:
0,1
мм,различия диаметров частиц не
существенны и в расчетные выражения
входят лишь элементы потока. Укажем две
формулы этого рода:
формула К.В. Гришанина
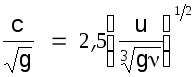 (1.20)
(1.20)
формула Г.Л. Гладкова
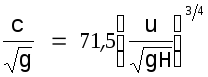 (1.21)
(1.21)
Обе формулы получены путем обработки натурных данных. Заметим, что средний и мелкий песок - это преобладающий род донного грунта у равнинных рек европейской территории России и Западной Сибири.
В задачах, касающихся деформируемых русел, уравнения, описывающие движение воды, дополняются уравнением баланса наносов и формулой расхода наносов. Уравнение баланса наносов, называемое также уравнением деформации, в одномерном случае записывается:
![]() (1.22)
(1.22)
Имеется много формул расхода наносов. В настоящее время наиболее употребительны следующие. Для крупнозернистых донных частиц (гравия и мелкой гальки) формула Э.Мейер-Петера и Р.Мюллера:
![]() (1.23)
(1.23)
Вошедшее в эту формулу критическое значение динамической скорости находится из выражения
![]() (1.24)
(1.24)
Для мелкозернистых донных частиц (0,1<d<2,0 мм.) применяют формулы Л.ван Рейна. Если наносы движутся во влекомом состоянии, расход наносов находится по формуле
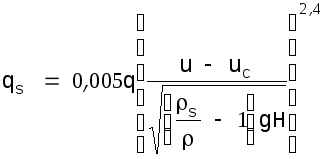 (1.25)
(1.25)
Если наносы движутся во взвешенном состоянии, формула (1.25) заменяется на формулу (1.25а).
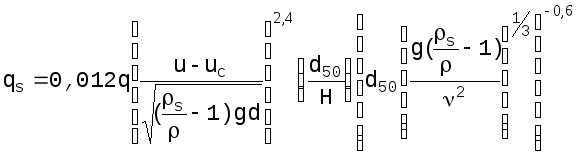
(1.25а)
Для величины критической скорости используются два выражения. При частицах диаметром 0,5<d<2,0 мм
![]() (1.26)
(1.26)
При частицах диаметром 0,1<d<0,5 мм
![]() (1.27)
(1.27)
Есть несколько формул, которые дают полный расход русловых наносов (т.е. сумму расходов влекомых и взвешенных частиц). Укажем формулу В.Графа и Е.Акароглу:
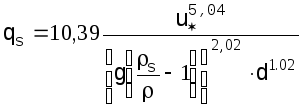 (1.28)
(1.28)
При
составлении формулы были использованы
измерения в лабораторных лотках в
естественных потоках и трубах. Величина
![]() выражает
полное сопротивление дна.
выражает
полное сопротивление дна.
При ориентировочных расчетах допустимо пользоваться в реках с песчаным дном упрощенной формулой
![]() (1.29)
(1.29)
Размерный коэффициент k следует находить по натурным измерениям расходов наносов или вычислять из наблюденных деформаций дна.
