5.4. Одновременная аппроксимация дифференциальных уравнений и краевых условий
В общем случае, т.е. когда точных сведений о краевых условиях нет, к невязке по области
на
(5.20)
добавляется невязка в краевых условиях
на
(5.21)
Можно попытаться уменьшить взвешенную сумму невязок по области и на границе, положив
,
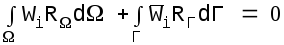(5.22)
где
весовые функции
и
могут быть выбраны независимо.
5.5. Кусочно-определенные базисные функции и метод конечных элементов
В методах аппроксимации, описанных выше, предполагалось, что базисные функции Nm, которые входят в разложение
,
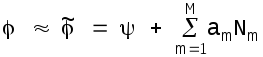(5.23)
определяются
одним выражением на всей области
,
а интегралы в аппроксимирующих уравнениях
(типа (5.6) или (5.22)) вычисляются сразу по
всей области. На практике гораздо чаще
оказывается необходимым разбить область
на ряд непрерывающихся подобластей или
элементов
и построить затем аппроксимации
кусочным образом, т.е. отдельно для
каждой подобласти. Используемые в
процессе аппроксимации базисные функции
также могут быть определены кусочным
образом с применением различных выражений
для разных подобластей. Определенные
интегралы, входящие в аппроксимирующие
уравнения, можно получить простым
суммированием их вкладов в каждой
подобласти:
,
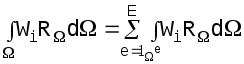(5.24)
,
(5.25)
При
условии, что
,
.
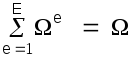Здесь Е - общее число элементов, на
которые разбивается область
,
а
- часть границы
,
лежащая на Г.
Т.о. суммирование, включающее
,
проводится только по тем элементам
,
которые примыкают к границе.
Если подобласти имеют относительно простую форму и базисные функции определяются однотипно, то операции описанным способом позволяют решать задачи с областями достаточно сложной формы. Это и есть главная идея метода конечных элементов. Кусочное определение базисных функций означает, что на границах элементов аппроксимирующие функции и их производные могут иметь разрывы.
5.6. Кусочно-постоянные и кусочно-линейные базисные функции
Рассмотрим
аппроксимацию произвольной функции
одной независимой переменной
методом поточечной коллокации. Заменим
для этого на участке
непрерывный график функции
последовательностью неперекрывающихся
отрезков
.
Аппроксимирующая функция будет, очевидно,
разрывной (рис.10). В качестве точек
коллокации выберем середины отрезков
.
Они будут называться узлами. Узлы и
элементы
занумеруем.
Функцию
,
аппроксимирующую заданную функцию
,
можно построить, приписав каждому узлу
m
значение кусочно постоянной, одинаковой
для всех элементов (глобальной) базисной
функции Nm.
Она равна единице на элементе m
и нулю на всех остальных элементах.
Таким образом,
в
(5.26)
Эта
формула получена из (5.23) путем замены в
точках коллокации величины am
величиной
и путем отбрасывания произвольной
функции
.
Последнее основано на том, что значения
функции
в граничных точках отрезка X=0, X=LX
приближаются сколь угодно точно к
заданным значениям за счет уменьшения
длин элементов, примыкающих к границам,
при предельном переходе.
На
каждом элементе е
глобальная аппроксимация может быть
выражена через значения
в узле элемента и базисной функции
элемента Nе
:
на
элементе е
(5.27)
Более
точное приближение можно получить,
используя не кусочно постоянные, а
кусочно линейные элементы. Пример
соответствующего графического построения
дан на рис.11. В этом случае нумерованными
узлами служат точки сопряжения соседних
элементов. Базисная функция
в узле i
и равна нулю во всех других узлах.
Глобальная аппроксимация записывается
в виде
в
(5.28)
Подстановка
соответствующих значений в узлах X=0,
X=LX автоматически
дает нужные значения на границах области
и явное использование функции
не требуется.
На
каждом элементе е
с узлами i
и j
аппроксимацию можно произвести с помощью
двух линейных базисных функций элемента
и узловых значений
,
следуя правилу
на
элементе е
(5.29)
Решим
теперь задачу методом Галеркина, т.е.
положив
.
Рассматривая отрезок оси X от 0 до 1,
получим основное уравнение метода
невязок в виде:
(5.30)
Считая аппроксимирующую функцию кусочно постоянной, можем написать:
(5.31)
и, сделав подстановку в (5.30):
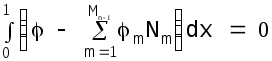(5.32)
Таким образом приходим к стандартной системе уравнений
Ka=f,
(5.33)
и
(5.34)
Компонента
вектора
это узловые значения аппроксимации
,
и следовательно, они совпадают с узловыми
значениями заданной функции. Фигурирующие
в (5.33) глобальные интегралы можно получить
посредством суммирования вклада
отдельных элементов, т.е. по формуле:
,
,
(5.35)
где
и
вычисляются путем интегрирования только
по одному элементу е.
Кусочно-постоянные и кусочно-линейные базисные функции можно применить и для аппроксимации функций на двумерных областях. Такая возможность представлена на рис.12 и 13, где рассматриваемая двумерная область разбита на треугольники. Снова применяется метод поточечной коллокации, причем в модели с кусочно-постоянными базисными функциями за узлы принимаются центры тяжести треугольников, а в модели с кусочно-линейными базисными функциями узлами служат вершины треугольников.
Многие реальные объекты имеют неправильные криволинейные очертания. Существуют способы отображения таких областей на области с прямоугольной сеткой, а значит, и на области, состоящие из треугольных ячеек. Операции отображения запрограммированы и могут осуществляться в автоматическом режиме. Это позволяет, в частности, сгущать сетку в местах с быстрым изменением функции. Пример отображения дан на рис.14