
- •1. Уравнения движения воды и наносов
- •2. Дискретизация уравнений.
- •3. Применение метода характеристик к
- •4. Метод конечных разностей
- •5. Метод конечных элементов
- •5.4. Одновременная аппроксимация дифференциальных уравнений и краевых условий
- •5.5. Кусочно-определенные базисные функции и метод конечных элементов
- •6. Калибровка модели
3. Применение метода характеристик к
расчету русловых деформаций
Кроме задач неустановившегося движения воды, метод характеристик применяется также к расчету деформаций продольного профиля дна руслового потока. Расчет производится с помощью одномерного уравнения баланса наносов (1.22). Это гиперболическое уравнение первого порядка имеет одно семейство характеристик. Русловые формы могут перемещаться или только вниз (обычный случай перемещения) или только вверх (случай попятной эрозии).
Мы ограничимся здесь простейшим случаем расчета деформаций за короткий промежуток времени, в течение которого расход воды и уровень свободной поверхности остаются неизменными. При этом условии перемещение русловых форм (побочней, осередков, островов) можно представить в виде движения вдоль потока некоторых фиксированных площадей поперечных сечений.
При неизменном уровне свободной поверхности, производную от средней высоты дна по времени можно заменить производной от средней глубины, взятой с обратным знаком:
![]() (3.1)
(3.1)![]()
Уравнение деформации примет вид:
![]() (3.2)
(3.2)
Воспользуемся формулой расхода влекомых наносов И.И. Леви. После перехода от удельного к полному расходу наносов в поперечном сечении и простых преобразований формула Леви примет вид:
![]() (3.3)
(3.3)
Рассматривая формулу (3.3), можно убедиться, что изменение площади поперечного сечения гораздо сильнее влияет на расход наносов, чем изменение диаметра донных частиц и средней глубины в сечении. Это позволяет, приняв приближенно
 ,
(3.4)
,
(3.4)
применять формулу расхода наносов в следующем упрощенном виде:
![]() (3.5)
(3.5)
Подстановка этого выражения в уравнение (3.2), с последующим дифференцированием, даст:
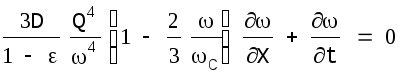 (3.6)
(3.6)
Это квазилинейное дифференциальное уравнение в частных производных первого порядка эквивалентно следующей системе двух обыкновенных уравнений
 (3.7)
(3.7)
 (3.8)
(3.8)
На фазовой плоскости (x,t) прямые, удовлетворяющие уравнению
![]() (3.9)
(3.9)
представляют
собой характеристики дифференциального
уравнения (3.8). Фиксированные площади
поперечных сечений движутся вдоль этих
прямых. Формула(3.8) выражает скорости
их движения. Последовательность расчетов
следующая: располагая распределением
площадей поперечных сечений потока на
начальный момент времени
![]() ,
выбираем расчетные сечения и вычисляем
по формуле (3.8) скорости их перемещения.
Дальнейший расчет удобно вести графически.
Зная начальное положение площадей
расчетных сечений и скорости их движения,
строим по формуле (3.9) линии характеристик.
Когда это сделано, простым отсчетом по
осям координат получаем новые
местоположения расчетных сечений на
любой момент времени, до которого
сохраняется условие неизменности
расхода воды. Более подробные сведения
см. в книге
,
выбираем расчетные сечения и вычисляем
по формуле (3.8) скорости их перемещения.
Дальнейший расчет удобно вести графически.
Зная начальное положение площадей
расчетных сечений и скорости их движения,
строим по формуле (3.9) линии характеристик.
Когда это сделано, простым отсчетом по
осям координат получаем новые
местоположения расчетных сечений на
любой момент времени, до которого
сохраняется условие неизменности
расхода воды. Более подробные сведения
см. в книге
Пример графического решения задачи представлен на рис.5
4. Метод конечных разностей
4.1. Основные понятия
В методе конечных разностей дискретизация уравнений достигается разбиением потока по длине на конечные участки (шаги по длине) и разбиением времени на конечные интервалы (шаги по времени). Поперечные сечения и моменты времени, определяющие границы шагов, нумеруются. Номер сечения дальше обозначается i , номер момента - k. Т.о., i=1,2,3,..., k=1,2,3,... Считается, что внутри назначенных шагов элементы движения изменяются линейно. На границах шагов производные по длине и времени могут терпеть разрыв.
Существует два способа деления потоков по длине. По первому из них граничные сечения проводят через середины участков возрастания или уменьшения площадей сечений. Изменение геометрических характеристик потока по его длине при этом сглаживается. Этот способ удобен тогда, когда падение свободной поверхности приравнивается потерям энергии на трение - ускорениями пренебрегают. По второму способу граничные сечения назначаются в местах с экстремальными значениями площадей поперечных сечений. Обычно это сечения на гребнях перекатов и в наиболее глубоких местах плесовых лощин (рис.6). Этот способ удобен в том случае, когда кривые свободной поверхности строятся с учетом ускорений. Его следует применять также при расчете русловых деформаций.
В результате выбора определенных сечений и моментов времени на фазовой плоскости (x, t) образуется прямоугольная сетка (рис.7). Она может быть неравномерной, как по длине, так и по времени. Величины в узлах сетки называются сеточными функциями.
Производные
записываются в виде отношений между
разностями близких значений функций к
разностям соответствующих значений
независимых переменных. Эти отношения
называются разностными схемами. Одна
и та же производная может аппроксимироваться
различными схемами. Так, для пространственной
производной
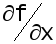 можно применить следующие разностные
схемы:
можно применить следующие разностные
схемы:
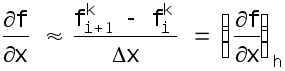 (4.1)
(4.1)
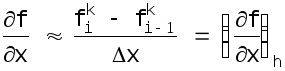 (4.2)
(4.2)
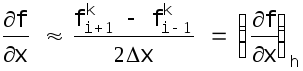 (4.3)
(4.3)
Здесь
 обозначает дискретную аппроксимацию
производной. Аналогичные выражения
пишутся и для производных по времени.
Сделанные записи не исчерпывают всех
возможностей.
обозначает дискретную аппроксимацию
производной. Аналогичные выражения
пишутся и для производных по времени.
Сделанные записи не исчерпывают всех
возможностей.
Для
оценки качества разностных схем, т.е.
их удобства и достоверности, используются
три показателя: порядок аппроксимации,
сходимость и устойчивость. Чтобы
установить порядок аппроксимации,
рассматриваемую функцию разлагают в
ряд Тейлора и дифференцируют. При каждом
члене полученного ряда стоит множителем
приращение независимой переменной,
например
![]() в некоторой степени m . Члены, начиная
с того, при котором множитель имеет
степень m = m0,
отбрасывают. Cумму отброшенных членов
обозначают
в некоторой степени m . Члены, начиная
с того, при котором множитель имеет
степень m = m0,
отбрасывают. Cумму отброшенных членов
обозначают
![]() .
Величина m0
называется порядком аппроксимации.
Так, если в разложении
.
Величина m0
называется порядком аппроксимации.
Так, если в разложении
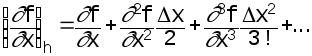 (4.4)
(4.4)
отбросить все члены, начиная со второго, т.е. признать
 ,
,
то мы найдем, что последнее выражение представляет аппроксимацию первого порядка. Нетрудно найти, что разностная схема
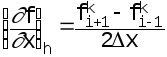
представляет аппроксимацию второго порядка. Если приращения переменных достаточно малы, то чем выше порядок аппроксимации, тем она точнее.
Под
сходимостью разностных уравнений
понимается условие, согласно которому
при сгущении разностной сетки, т.е. при
неограниченном уменьшении шагов
независимых переменных, решения этих
уравнений приближаются к точному
решению. Однако осуществить прямую
проверку сходимости мы не можем, т.к.
точных решений у нас нет. Выход из этого
положения дает теорема Лакса, согласно
которой необходимое и достаточное
условие сходимости разностных уравнений
состоит в устойчивости их решений.
Устойчивыми считаются решения, имеющие
ограниченные результаты. В некоторых
случаях устойчивость уравнений удается
обеспечить, введя в них так называемые
весовые коэффициенты
![]() ,
,
![]() .
.
В
методе конечных разностей последовательно
выполняемые расчеты состоят из переходов
от некоторого данного временного уровня
k к следующему k+1. Техника этих переходов
различна у двух классов разностных
схем: явных и неявных. При явных схемах,
чтобы узнать значение функции
![]() ,
достаточно располагать значениями
функции f лишь в нескольких ближайших
точках (i-1, i, i+1) в момент времени k. Решение
этой локальной задачи не зависит от
состояния дел на остальном протяжении
оси x . При неясных схемах картина другая.
Здесь производная по длине аппроксимируется
разностью функций не в слое k, где все
известно, а в слое k+1, где все не известно.
Это приводит к появлению в разностной
схеме лишней неизвестной, и уравнение
связи оказывается незамкнутым. Лишнюю
неизвестную приходится определять по
данным из следующего шага по длине. Так
возникает цепочка взаимосвязанных
уравнений, замкнуть которую можно лишь
с помощью граничного условия на нижнем
конце рассматриваемого потока. Нередко
оказывается, что число неизвестных,
которые надо определить в нижнем
замыкающем сечении, больше числа
имеющихся граничных условий. В этом
случае на последнем шаге прибегают к
методу характеристик.
,
достаточно располагать значениями
функции f лишь в нескольких ближайших
точках (i-1, i, i+1) в момент времени k. Решение
этой локальной задачи не зависит от
состояния дел на остальном протяжении
оси x . При неясных схемах картина другая.
Здесь производная по длине аппроксимируется
разностью функций не в слое k, где все
известно, а в слое k+1, где все не известно.
Это приводит к появлению в разностной
схеме лишней неизвестной, и уравнение
связи оказывается незамкнутым. Лишнюю
неизвестную приходится определять по
данным из следующего шага по длине. Так
возникает цепочка взаимосвязанных
уравнений, замкнуть которую можно лишь
с помощью граничного условия на нижнем
конце рассматриваемого потока. Нередко
оказывается, что число неизвестных,
которые надо определить в нижнем
замыкающем сечении, больше числа
имеющихся граничных условий. В этом
случае на последнем шаге прибегают к
методу характеристик.
Из сказанного видно, что вычисления по неявным схемам имеют большую трудоемкость, чем вычисления с явными схемами. Однако, вследствие коренного недостатка явных схем, о котором будет говориться в следующем пункте, эти схемы применяются гораздо реже, чем неявные.
4.2. Некоторые явные схемы.
Уравнения речной гидравлики допускают следующую обобщенную запись:
 ,
(4.5)
,
(4.5)
где f = f(x,t). Так, в уравнении количества движения f = u, а все остальные члены зависят от u и объединяются функцией G. Различия разностных схем - это различия в записи производных. Одной из первых появившихся явных разностных схем была схема, получившая название ”чехарда”. В ней производные были записаны в следующей симметричной форме:
 (4.6)
(4.6)
 (4.7)
(4.7)
Подстановка этих выражений в уравнение (4.3) позволяет без добавочных выкладок написать искомое выражение функции f в слое k+1:
![]() (4.8)
(4.8)
Более сложное выражение для производной по времени выбрал Лакс:
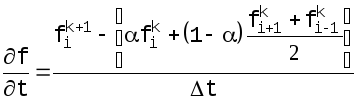
![]() (4.9)
(4.9)
Весовой коэффициент был принят Лаксом равным 0,5.
Пространственная производная имеет такой же вид, как в схеме ”чехарда”:
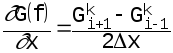
Подстановка этих выражений в уравнение (4.5) дает:
![]()
![]() (4.10)
(4.10)
Решения разностных уравнений неустановившегося движения, полученные с помощью явных схем, оказываются устойчивыми лишь в определенной области отношений между шагами по длине и по времени. Это ограничение выражается условием Куранта-Фридрихса-Леви (КФЛ):
 (4.11)
(4.11)
Для равнинных рек, с их небольшими скоростями, но большими глубинами, при шагах по длине, измеряемых сотнями метров, шаги по времени получаются неприемлемо малыми. Поэтому применять явные схемы в задачах неустановившегося движения нежелательно. Областью их применения остается сравнительно узкая область расчета русловых деформаций, где характерной скоростью служит скорость перемещения русловых форм. Она на несколько порядков меньше волновой скорости.
4.3. Некоторые неявные схемы
Еще на заре развития численных методов, в 1961г., А. Прейсман предложил разностный метод решения уравнений Сен-Венана, основанный на неявных схемах, с применением двух весовых коэффициентов. Выражения для производных были приняты следующие:
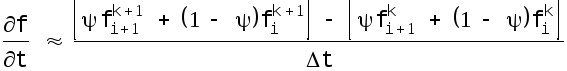 (4.12)
(4.12)
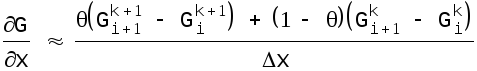 (4.13)
(4.13)
Для
весового коэффициента
![]() Прейсман принял постоянное значение
равное 1/2. Коэффициент
Прейсман принял постоянное значение
равное 1/2. Коэффициент
![]() был принят переменным в пределах от 0,5
до 1,0. При
был принят переменным в пределах от 0,5
до 1,0. При
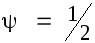 выражение для производной по t принимает
вид:
выражение для производной по t принимает
вид:
 (4.14)
(4.14)
Целью расчета в этой одномерной задаче становится отыскание значений расхода воды и площади поперечного сечения во всех точках разностной сетки. Если число участков равно N, то для каждого момента времени должны быть найдены 2N-2 линейных алгебраических уравнений не составит большого труда (не займет много времени), даже если N составляет несколько сотен.
Та же задача решалась группой сотрудников Института гидродинамики СО АН СССР под руководством О.Ф.Васильева. Уравнение движения было преобразовано к виду закона сохранения. При этом волновая скорость входит в уравнение движения в явном виде. Была использована следующая аппроксимация производных:
 (4.15)
(4.15)
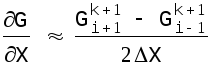 (4.16)
(4.16)
Как видно (см.рис.8), для определения производных по t и по x используются разные пары точек.
В схеме Гунаратнама-Перкинса производная по длине вычисляется также, как в схеме Васильева, т.е. по формуле (4.16), а производная по времени определяется сложным выражением:
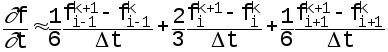 (4.17)
(4.17)
Здесь три точки, взятые вдоль потока, связаны с двумя точками на оси времени. Это приводит к системе, состоящей из 2N-4 уравнений с 2N неизвестными. Система замыкается с помощью двух граничных условий и двух уравнений характеристик, записанных на концах потока.
Существует еще несколько разностных схем, хорошо апробированных в расчетах. В России традиционно используются схемы Васильева. Применительно к ним разработан ряд программ машинного счета. В них предусмотрены разнообразные добавочные потребности пользователя: расчет при делении и соединении потоков, учет бокового притока или оттока, учет аккумулирующих емкостей.
Численное решение задачи о распространении паводка с применением метода конечных разностей впервые было выполнено Дж.Стокером на примере р. Огайо, в 1953г. Однако отдельные попытки численных решений восходят к концу XIX столетия. В нашей стране начало этим разработкам положил О.Ф. Васильев (1963г.).
4.4. Применение метода конечных разностей
к расчету русловых деформаций
Решая
задачу об одномерных русловых деформациях,
т.е. задачу об изменении продольного
профиля дна руслового потока, мы должны
использовать три уравнения: уравнение
количества движения воды, уравнение
баланса объемов воды (уравнение
неразрывности) уравнение баланса объемов
наносов (уравнение деформации), плюс
две вспомогательные зависимости: закон
сопротивления и формулу расхода наносов.
Разбиение потока на расчетные участки,
как уже указывалось, удобно вести,
используя сечения с экстремальными
значениями площади. Если такие участки
получаются чересчур длинными, ничто не
препятствует проведению добавочных
сечений. Сложнее обстоит дело со временем,
т.к. две характерные скорости - скорость
движения воды и скорость перемещения
русловых форм - имеют разный порядок.
Скорость форм меньше скорости воды в
10000 раз (в среднем). Можно, конечно, не
обращать на это внимания, делая вид, что
все нормально, но лучше все же использовать
способ расщепления, т.е. ввести разные
масштабы времени для потока и для дна.
Практически это означает следующее:
начиная расчет, а его следует вести в
явной схеме, мы на первом или на нескольких
начальных шагах рассчитываем движение
воды, считая дно недеформируемым. Затем
определяем расход наносов на конец
первого шага (или нескольких начальных)
и подсчитываем деформацию, т.е. величину
![]() .
Если она не превышает погрешности
промеров глубин (0,05-0,10 м), продолжаем
расчет тем же порядком. Если деформация
превышает погрешность промеров,
производим пересчет, уменьшив интервал
времени. Такой способ расчетов
преувеличивает интенсивность колебаний
высоты дна в малом , но крупномасштабные
колебания воспроизводит с достаточной
точностью. Оговоримся, что речь идет о
деформациях естественного русла, в
котором мелкие места чередуются с
глубокими. Также, как в главе 3, ограничимся
случаем короткого периода времени, в
рамках которого расход и уровень воды
не изменяются. Дифференциальное уравнение
деформации имеет при этом вид формулы
(3.2). Зависимой переменной в нем служит
площадь поперечного сечения потока
.
Если она не превышает погрешности
промеров глубин (0,05-0,10 м), продолжаем
расчет тем же порядком. Если деформация
превышает погрешность промеров,
производим пересчет, уменьшив интервал
времени. Такой способ расчетов
преувеличивает интенсивность колебаний
высоты дна в малом , но крупномасштабные
колебания воспроизводит с достаточной
точностью. Оговоримся, что речь идет о
деформациях естественного русла, в
котором мелкие места чередуются с
глубокими. Также, как в главе 3, ограничимся
случаем короткого периода времени, в
рамках которого расход и уровень воды
не изменяются. Дифференциальное уравнение
деформации имеет при этом вид формулы
(3.2). Зависимой переменной в нем служит
площадь поперечного сечения потока
![]() .
.
Для записи разностного уравнения воспользуемся левой трехточечной схемой:
![]()
(4.18)
Различие
между левой и правой схемами позволяет
весьма просто продемонстрировать
влияние вида схемы на ее устойчивость.
Пусть, назначая расход наносов
![]() ,
мы ошибались и преувеличивали этот
расход. В результате, на следующем шаге
по времени площадь
,
мы ошибались и преувеличивали этот
расход. В результате, на следующем шаге
по времени площадь
![]() окажется завышенной и, значит, скорость
течения, а с ней и расход наносов
окажется завышенной и, значит, скорость
течения, а с ней и расход наносов
![]() ,
будут занижены. Ошибка, допущенная на
предшествующем шаге, будет в какой-то
мере ослаблена. Это свидетельствует об
устойчивости разностной схемы (4.18).
,
будут занижены. Ошибка, допущенная на
предшествующем шаге, будет в какой-то
мере ослаблена. Это свидетельствует об
устойчивости разностной схемы (4.18).
При использовании правой трехточечной схемы имеем:
![]() (4.19)
(4.19)
Если
расход наносов в сечении xi
завышен, это приведет к тому, что в момент
tкн
площадь
![]() окажется заниженной, а скорость течения
и расход Qs
завышенными. Ошибка будет не сглаживаться,
а нарастать. Правая трехточечная схема
неустойчива. Такой результат есть
следствие прямой связи между расходом
наносов и скоростью течения.
окажется заниженной, а скорость течения
и расход Qs
завышенными. Ошибка будет не сглаживаться,
а нарастать. Правая трехточечная схема
неустойчива. Такой результат есть
следствие прямой связи между расходом
наносов и скоростью течения.
Надежность получаемых результатов определяется точностью используемых выражений для расхода наносов. Краткие рекомендации по этому поводу были даны в гл.1. Они применимы при незатопленной пойме. При выходе потока на пойму взвешенные русловые наносы из-за уменьшения скоростей осаждаются, давая начало образованию прирусловых валов. Осаждение внерусловых наносов увеличивает толщину наилка - очень тонкого слоя мелких частиц, покрывающего всю пойму. Рассчитать расход наносов на пойме крайне трудно. Ту часть расхода наносов, которая проходит в русле, удается найти лишь тогда, когда направления движения воды в русле и на пойме или совпадают, или близки.
4.5. Решение двумерных задач
Решая двумерные задачи методом конечных разностей, поток разбивают в плане на несколько (от 3 до 10) плоских струй. В плесовых лощинах трением между этими струями пренебрегают. На перекатах желательно его учитывать. Учет трения между струями становится обязательным на участках отрывного расширения потока, где неравномерность распределения скоростей поперек потока очень велика. Движение считается установившимся.
Чтобы определить границы струй, надо построить на участке потока систему плановых линий тока. Удобно при этом считать, что между каждыми двумя смежными линиями тока проходит один и тот же расход воды. Струи с таким свойством называются равнорасходными. Совокупность линий тока и ортогональных им поперечников называется планом течений (рис.9). Если линии тока криволинейные, то и ортогональные поперечники получаются криволинейными.
Построение
планов течений встречается с наибольшими
трудностями на перекатах, где рельеф
дна бывает сложным. Трудности здесь
связаны не столько с кривизной линий
тока, сколько с их расходимостью.
Применительно к этому случаю К.В. Гришанин
разработал модификацию метода Бернадского,
которую мы дальше изложим. Задача
решается путем последовательных
приближений. Исходным служит уравнение
(1.17). Пренебрегая трением на боковых
поверхностях струй, исключив, с помощью
уравнения неразрывности (1.15), производную
 и умножив все члены уравнения на глубину
вертикали h, будем иметь:
и умножив все члены уравнения на глубину
вертикали h, будем иметь:
![]() (4.20)
(4.20)
откуда:
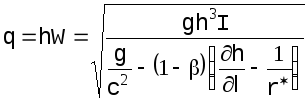 (4.21)
(4.21)
Для
дальнейшего расчета необходимо знать
расход воды в реке. Коэффициент Шези
С, коэффициент
![]() и иметь план русла в изобатах при
наполнении, отвечающем данному расходу.
В первом приближении уравнение (4.21)
заменяется уравнением равномерного
движения:
и иметь план русла в изобатах при
наполнении, отвечающем данному расходу.
В первом приближении уравнение (4.21)
заменяется уравнением равномерного
движения:
![]() (4.22)
(4.22)
Продольный
уклон свободной поверхности поперек
потока не изменяется. В главе 1 было
указано, что если постоянным в поперечном
сечении является и коэффициент Шези,
то удельные расходы распределяются
поперек русла пропорционально глубинам
в степени 3/2. Это простое условие так
же, как и немного более сложное условие
постоянного коэффициента шероховатости,
делает возможным известное графическое
решение задачи, предложенное впервые
М.А. Великановым. Оно заключается в
следующем: разбиваем на участке ряд
поперечников, строим над каждым из них
эпюру подынтегральной функции
![]() ,
строим интегральные кривые
,
строим интегральные кривые
![]() ,
(4.23)
,
(4.23)
делим их конечные ординаты на равные части и, снеся точки деления на интегральные кривые, а с них на горизонтальные линии свободной поверхности, получаем деление поперечных сечений на части, пропускающие равные расходы воды. На плане участка соединяем плавными кривыми точки деления поперечников, и построение плана течений в первом приближении закончено.
Теперь
обращаемся к уравнению (4.21), переписывая
его в конечных разностях. Номера
поперечных сечений обозначаем i, номера
линий тока j . Коэффициент Шези считаем
в поперечном сечении постоянным.
Коэффициенту ![]() придаем
постоянное значение 0,3. Уклон I зависит
только от продольной координаты, т.е.
на каждом криволинейном поперечнике
он постоянный. Помня, что независимая
переменная
придаем
постоянное значение 0,3. Уклон I зависит
только от продольной координаты, т.е.
на каждом криволинейном поперечнике
он постоянный. Помня, что независимая
переменная
![]() изменяется вдоль линии тока, а независимая
переменная b - вдоль поперечников, пишем:
изменяется вдоль линии тока, а независимая
переменная b - вдоль поперечников, пишем:
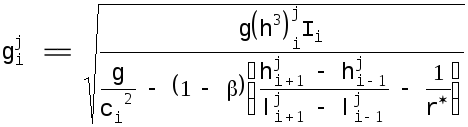 ,
(4.24)
,
(4.24)
где радиус кривизны поперечников вычисляется по двум формулам
![]()
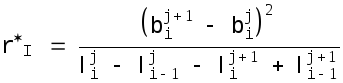 (4.25а)
(4.25а)
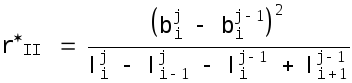 (4.25b)
(4.25b)
В формулу (4.24) подставляется среднее из двух значений. Формулы(4.25) основаны на замене малого угла между касательными к линии поперечника тангенсом угла между линиями тока. Когда расчеты по формуле (4.24) закончены, вычисляется полный расход воды
![]()
![]()
Если разность между рассчитанным расходом и заданным превышает допустимую погрешность, расчет повторяется. При каждом последующем приближении распределение глубин поперек потока берется по данным предшествующего приближения.
