5. Метод конечных элементов

5.1. Общие положения

Метод конечных элементов сильно отличается от метода конечных разностей. В нем также совершается переход от непрерывного к дискретному представлению явления, но способы этого перехода другие. Так, например, можно заменить неизвестную непрерывную функцию другой, тоже непрерывной, но более простой и имеющей известное уравнение. Дискретность такого представления будет состоять в том, что значения модельной функции будут лишь в конечном числе точек совпадать со значениями прототипа. Поэтому, говоря о методе конечных элементов, вместо термина дискретизация чаще пользуются термином аппроксимация.

Метод конечных элементов имел долгую историю. В начале в его основе лежал вариационный принцип. Задачей расчетов являлась минимизация некоторого функционала. Метод применялся преимущественно к решению задач теории упругости. С течением времени произошли, независимо друг от друга, два важных изменения. Во-первых, расширилась область применения - она стала охватывать и широкий круг вопросов механики жидкостей. Во-вторых, было понято, что прямое применение метода приближенного решения дифференциальных уравнений, предложенного в начале XX столетия Галеркиным, освобождает от необходимости пользоваться вариационными методами. В настоящее время опорой метода конечных элементов служит метод Галеркина. Для того чтобы его понять, надо познакомиться с двумя основными понятиями метода конечных элементов: базисными функциями и взвешенными невязками.

5.2. Базисные функции

Пусть требуется аппроксимировать заданную функцию в некоторой области , ограниченной замкнутой кривой Г. Начнем с того, что попытаемся найти функцию , которая в ряде граничной кривой Г принимала бы те же значения, что . Это условие назовем условием поточечной коллокации и обозначим . Введя систему линейно независимых базисных функций , таких, что для всех m, можем предложить аппроксимацию:

, (5.1)

где a_m(m=1,2,3,...M) - параметры, вычисляемые так, чтобы получить хорошее приближение. Система базисных функций должна обладать тем свойством, что комбинация 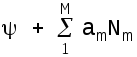, при , должна сколь угодно точно представлять произвольную функцию , удовлетворяющую условию . Это свойство называют условием полноты. Эта ситуация иллюстрируется рис.5, на котором область представлена отрезком , а базисные функции N_m разрывны. Они равны единице на каждом интервале и нулю - вне его.

Увеличивая число интервалов до бесконечности, получим непрерывную кривую. В качестве второго примера аппроксимации с помощью базисных функций рассмотрим применение с этой целью усеченных рядов Фурье. Если есть непрерывная кусочно-дифференцируемая функция, а есть линейная функция, принимающая те же значения, что , при X=0, и X=L_X, то бесконечный ряд

, (5.2)

коэффициенты которого определены равенствами

, (5.3)

сходится всюду на к значению функции . Обрывая ряд (5.2) на конечном числе М членов, получаем аппроксимацию

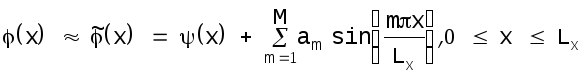(5.4)

5.3. Аппроксимация с применением

взвешенных невязок

Введем погрешность или невязку в аппроксимации

, (5.5)

считая функцией координат точки из . Чтобы уменьшить невязку во всей области , приравняем нулю интегралы от погрешности, взятые с различными весами

;=1,2,..M, (5.6)

где - множество линейно независимых весовых функций. Подставив в (5.6) выражение для по (5.1)

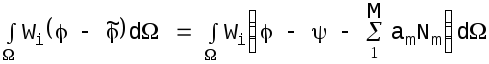(5.7)

видим, что система уравнений метода взвешенных невязок (5.6) сводится к системе линейных алгебраических уравнений для неизвестных коэффициентов а_m. Эту систему можно кратко записать в следующем виде:

Ка=f, (5.8)

(5.8a)

, (5.8b)

, (5.8c)

Таким образом, если известна аппроксимируемая функция , определена функция и выбраны системы базисных и весовых функций, то решая систему (5.8), можно получить коэффициенты аппроксимации (5.1).

Возможно различное задание весовых функций, а отсюда и разные способы аппроксимации с применением взвешенных невязок. Рассмотрим некоторые из этих способов.

Способ поточечной коллокации

Здесь элементы системы весовых функций задаются формулой:

, (5.9)

где в правой части стоит дельта-функция Дирака, обладающая свойствами:

, при

, при (5.10)

Выбор таких весовых функций означает, что невязка равна нулю в ряде заданных точек . При этом матрица К и вектор f в (5.8) имеют элементы:

, (5.11)

Коллокация по подобластям

Если весовые функции имеют вид

(5.12)

то уравнения (5.6) эквивалентны требованию равенства нулю интеграла от погрешности по каждой из М подобластей основной области. Для завершения аппроксимации нужно только решить систему (5.8), где

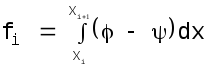, (5.13)

Метод Галеркина

В этом методе, играющем в настоящее время ведущую роль при использовании взвешенных невязок, в качестве весовых функций принимаются сами базисные функции:

(5.14)

В системе (5.8) матрица К и вектор f имеют при этом элементы:

, (5.15)

Можно показать, что представление функции с помощью усеченных рядов Фурье есть операция, эквивалентная применению метода Галеркина.

Можно показать, что известный метод наименьших квадратов также представляет собой частный случай применения концепции Галеркина. Действительно, согласно этому методу, требуется минимизировать интеграл от квадрата погрешности по области . В нашем случае надо найти минимум

, (5.16)

для чего полагается

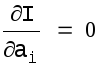, i=1,2,...,M (5.17)

Дифференцируя и замечая, что по(5.1)

, (5.18)

можем найти, что I достигает минимума при условии

(5.19)

Это соотношение совпадает с основным уравнением метода взвешенных невязок (5.6): с весами ,то есть, удовлетворяет процедуре метода Галеркина.