15.5 Наиболее важные операторы

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Конспект Клемешева.pdf

Скачиваний:

Добавлен:

21.03.2016

Размер:

10.86 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2517 18 19 20 21 22 23 24 25 > Следующая >>>

тогда справедливо равенство

.pO qO

qO pO / D

.q /

;

2 j @q

2 j

т.е.

pO qO

qO pO

(159)

2 j

Отсюда следует соотношение неопределенностей

p q >

(160)

.x; t / D Ae

Если известно классическое выражение физической величины как функции координат и импульса, то можно образовать соответствующий квантовомеханический оператор: в классическое выражение подставить операторы координат и импульса. В табл. 1 содержатся наиболее важные операторы, а также некоторые соотношения между ними.

К этой таблице следует добавить ряд замечаний. Оператор, характеризующий абсолютное значение момента количества движения, коммутирует с каждой компонентой и с оператором энергии, в то время как отдельные операторы компонент некоммутативны. Отсюда следует, что одновременно могут быть определены лишь энергия, абсолютное значение количества движения и одна из компонент, например z-компонента. Легко заметить, что собственная функция, характеризующая энергию,

Ylm D ej m' Plm.cos #/

(161)

является собственной функцией и оператора

O z , и оператора

, т.е. справедливо выра-

жение

(162)

D 2 j Yl

2 mYl

O z Yl

Собственным значением в этом случае является величина .h=2 /m. Если уравнение

(49) § 2-4 умножить на	.h=2 /2 и подставить из таблицы выражение L2								, то получим:
(49) § 2-4 умножить на								O
		2			h	2
	L	2	m		h	l.l		1/Y m:	(163)
			m
			Yl	D	2		C
	O		Yl	D	2		C	l

Здесь собственным значением является величина .h=2 /2l.l C1/. Это приводит к уже упоминавшемуся в § 2-1 пространственному квантованию, т.е. доказывает, что момент количества движения в выделенном направлении равен .h=2 /m (m принимает значение от — l до Cl ) и что абсолютное значение момента количества движения выражается в


виде .h=2 /		l.l C 1/.
число m по праву называют магнитным квантовым числом, будет объяснено
Почему	p

ниже.

130

Таблица 1. Операторы важнейших физических величин

Физическая

Классическое

Оператор

Замечания

величина

выражение

xO D x

Предписываемой

опера-

x; y; z

цией

является

простое

Координата

yO D y

умножение.

zO D z

Операторы — коммутатив-

ные.

pO x D

pO x pOy

pOy pO x D 0

и т.д.

2 j @x

Импульс

px ; py ; pz

pOy D

pO x xO O x pO x D

и т.д.

2 j @y

2 j

pO z D

pO x yO O y pO x D 0 и т.д.

2 j @z

2 j

Компоненты

Lx Ly

Ly Lx

Lx D ypz

zpy

2 j

момента

количества

zpx

xpz

x @y

y @x

O z

2 j

Ly Lz

Lz Ly

j 2 Lx

сферических

движения

Lz Lx

Lx Lz

координатах

2 j @'

O z D

Абсолютное

D O x

C O y

O z

значение

В сферических

координатах

L L

момента

O x

L L2

L2 L

количества

Lx C Lz

C Lz

O y

O y D 0

sin # @t

движения

L Lz

sin #

sin2 #

@'2

L2 H

H L2

O y

O O y

Оператор

O x

L H

H L

Гамильтона

O D

8 m

L H

H L

(гамильто-

i C

W .x; y; z/

H L

pz CWp .x; y; z/

O z

O O z

ниан)

@y2

@z2

В силовом поле с централь-

ной симметрией

Энергия

h @

—

2 j @t

131

16 Матричная форма квантовой механики

Оператор O , представляющий любую физическую величину, можно изобразить в

виде матрицы, представляющей данную величину аналогично оператору. Запишем урав-

нение для собственных значений оператора O

	O			D g					(164)
	G			P					(164)
			D	P
в форме полного ортогонального ряда			D		c ' , т. е.
X	O	' D				X
c	O	' D			g			:	(165)
	G				g	c	'	:	(165)

Если теперь обе части скалярно умножить на ' то соотношение, характеризующее ортогональность, примет вид:

' / D gc :

c .' ; O

(166)

Произведя замену

.' ; O ' / D O , получим:

(167)

O D

Последнее равенство можно переписать в форме

ı g/c

(168)

Более подробная запись этого равенства имеет вид:

.G11 g/c1 C G12c2 C G13c3 C ::: C G1ncn C ::: D 0I

G21c1 C .G22 g/c2 C G23c3 C ::: C G2ncn C ::: D 0I

: : :	(169)
Gn1c1 C Gn2c2 C Gn3c3 C ::: C .Gnn	g/cn C ::: D 0I
: : :

Неизвестные коэффициенты образуют систему уравнений, которая имеет нетриви-

альное решение только при условии равенства нулю ее детерминанта:
G ı g D 0:		(170)
Это так называемое секулярное уравнение	для определения интересующего нас соб-

ственного значения g. Здесь G образуют совокупность чисел, которые можно упорядочить в виде двумерного бесконечного набора чисел. Последний может рассматриваться как квадратная матрица (бесконечная), характеризующая заданную физическую величину. В действительности вышеописанным способом для заданной матрицы могут быть определены собственные значения. Нетрудно убедиться, что такая матрица подчиняется правилам матричного исчисления: матрица, полученная в результате матричного умножения, соответствует произведению операторов, и если оператор самосопряженный, то

такой же будет и матрица: Gij D O .

Gj i

132

Если матрица G составлена из собственных функций оператора O		, то для каждого
	G	G			и,
			D
элемента ортогональной системы функций справедливо соотношение		O '		g '
следовательно,	D .' ; O ' / D .' ; g ' / D g .' ; ' / D ı g :
G				(171)
	G

Эта матрица является диагональной, причем ее диагональные элементы дают последовательность отдельных собственных значений. Именно поэтому преобразование матриц к диагональному виду имеет такое большое значение в матричной механике.

Переход к матричной форме иллюстрируется на примере линейного гармонического осциллятора. Рассмотрим такую заведомо классическую модель, как колеблющаяся система, состоящая из тела и пружины. Потенциальная энергия системы Wp D 12 kx2 (где k — постоянная пружины). Уравнение Шредингера имеет в этом случае вид:

.x/

8 2m

.x/ D 0:

(172)

dx2

Это уравнение можно переписать в виде

d 2

. /

D .

2/ . / D 0;

(173)

d 2

4 mk4 2

4 W m 1=2

1=2

где D ˛x; ˛

;

, a

=2 выражает классиче-

скую частоту.

Находим решение этого уравнения в виде

. / D H . /e 21 2 :

(174)

Тогда для H . / получится дифференциальное уравнение

H 00

2 H 0 C .

1/H D 0

(175)

— эрмитово дифференциальное уравнение, решением которого являются полиномы Эрмита. Их получают следующим образом.

Представим H . / как степенной ряд (см. случай полиномов Лагерра):

H . / D s .a0 C a1 C a2 2 C : : :/; a0 ¤ 0; s > 0:

(176)

Точка D 0 во всех случаях дает конечное значение. Подставляя ряд в дифференциальное уравнение и группируя члены с одинаковыми степенями, приравниваем их нулю. В результате получаются следующие рекуррентные формулы для коэффициентов:

		s.s		1/a0 D 0I						>
			C	C			C		D I	>
		.s	C	1/sa1	D 0I		C		D I	9
			C	C			C		D I	=
		.s C		2/.s	1/a2	.2s 1		/a0	0	>	(177)
										>
		.s 3/.s 2/a3				.2s 3 /a1			0	>
		.s 3/.s 2/a3				.2s 3 /a1			0	>
		.s C C 2/.s C C 1/a C2								>
		.s C C 2/.s C C 1/a C2						.2s C 2 C 1 /a D 0: >
Примем a	0	¤	0, это значит, что				s равно нулю или единице. Из			второго уравнения
							s равно нулю или единице. Из			;

следует, что s D 0, либо a1 D 0, либо a1 D s D 0. Так как при бесконечно большом числе членов получаем величину a C2=a ! 2= , растущую быстрее, чем e 2 , то очевидно,

133

что -функция станет равной нулю уже при конечном числе членов полинома H . /. Если

2s C 2 C 1 D 0I D 2s C 2 C 1;

(178)

то члены a C2, a C4 равны нулю; должно быть четным числом. Если — нечетное число, то при условии a0 ¤ 0 все члены a2; a4 : : : должны были бы быть отличными от нуля, ряд не обрывался бы на конечном числе членов, несмотря на то, что ряд, относящийся к нечетному a обрывается. С другой стороны, если при выборе четным члены с четным индексом «обрываются», то расхождение нечетных можно предотвратить, задавая a0 D 0, что дает a3 D a5 D a7 D : : : D 0; подставив D 2k, можно получить:

D 2s C 4k C 1:

(179)

Если принять s D 0 или s D 1, то D 4k C 1 или D 4k C 3.

Если k равно 0, 1, 2,. . . , из первого равенства получаем числа 1, 5, 9, 13,. . . , из

второго — 3, 7, 11, 15,. . . , т.е. ряд значений :
D 2n C 1; n D 0; 1; 2; : : :	(180)

При этих значениях существует одно решение дифференциального уравнения, превращающееся в нуль на бесконечности. Если учесть также выражение D 2W = h , то для возможных энергетических значений получим:

Wn D h n C	1	:	(181)
	2

Для отдельных полиномов Эрмита рекуррентная формула выражается следующим образом:

H0. / D 1I		H3. / D 8 3	4		12 I	2	3C 12I
H1	. / D 2 I2	H4. / D 16		5	48		3C 12I	(182)
H2	. / D 4	2I H3. / D 32			160		C 20 :

Решение, относящееся к собственному значению Wn, имеет вид:

		n. / D NnHn.˛x/e 12 ˛2 x2					un.x/:				(183)
Целесообразно ввести нормировку:
C1		C1	2	2			Nn	2	C1	2
Z j	n.x/j2 dx D jNnj2	Z Hn2	.˛; x/e ˛	x	dx D	j	j		Z Hn2	. /e	d D 1: (184)
						j	j
							˛
1		1							1

Несколько громоздкий, но не представляющий принципиальных затруднений расчет дает выражение для нормирующего множителя:

Nn D	˛	1=2	:	(185)

	1=22nn!
Собственные функции удовлетворяют условию ортогональности
C1
Z
Hn. /Hm. /e 2 d D 0;			n ¤ m:	(186)
1

134

Для заданных собственных функций путем сложных вычислений можно определить элементы матрицы оператора координаты qO D x:

1 nC1

при m

qnm

.x/x

m.x/dx

(187)

2m! n

при m

в остальных случаях.

ˆ0

Матричные элементы оператора pO D

имеют вид:

2 j

2 j dx

D r 2

pnm

n.x/ h

m.x/dx

! m

j .n

1/ 2

при m

8j n 2

при m D n C

1 I

в остальных случаях.

(188)

Непосредственное вычисление показывает, что обе матрицы удовлетворяют переста-

новочному соотношению и диагонализируют матрицу энергии

2 bI

(189)

1 h

23 h

2 h

(190)

n 1

При рассмотрении задачи о линейном осцилляторе мы исходили из уравнения Шредингера и частного решения этого уравнения, и пришли, таким образом, к матрицам, удовлетворяющим перестановочному соотношению и диагонализирующим матрицу Гамильтона. Однако можно выбрать и другой путь, в котором четко проявятся независимость и равнозначность и волновой механики Шредингера, и матричной механики Гейзенберга. Справедливо утверждение, что если существуют две самосопряженные

матрицы p и q, удовлетворяющие перестановочному соотношению

pq qp D	h	(191)
	2 j 1

и превращающие матрицу H в диагональную, то ее диагональные элементы дают собственные значения энергии.

Для обсуждения в дальнейшем задачи квантования различных полей излучения целесообразно переписать оператор Гамильтона для осциллятора.

Для этого введем операторы aO и aO+, определенные следующим образом:

pO x D

1 @

xO C

x C

2~˛

2˛

aO+ D

1 @

pO x D

2~˛

2˛

135

Тогда, во-первых, легко выразить через них операторы xO и pO x :

xO D	1		.aO+ C aO/I
	p

2˛

~˛

pO x D j p .aO+ aO/I

и, во-вторых, доказать справедливость перестановочного соотношения

aO+ aO aO aO+ D 1:

, имеет вид:

Оператор Гамильтона O , выраженный через

и O

O D 2

O O O

aO C 2

a a

Несколько труднее доказываются утверждения

aO+ un D p

n C 1unC1I

n 1

;

a u

pnu

где un задается уравнением (183).

Эти соотношения определяют оператор aO+ как оператор рождения и aO как оператор уничтожения.

Чтобы доказать эти равенства, требуется показать, что функции aO+ un и aO un удовлетворяют уравнению Шредингера с собственными значениями WnC1 и Wn 1.

Оператор aO+ aO обладает свойствами:

; . O

D 0I

a+ a

a+.p

a+.a u

n 1

O n

D O

Следовательно, собственные значения aO+ aO представляют собой квантовые числа 1,

2, . . . , n. Отсюда следует, что

aO aO C 2

n D

C 2

O un D

! n

u :

Таким образом, мы опять пришли к представлению о собственных значениях.

136

17Решение уравнения Шредингера для свободного электрона

Вэтом случае уравнение Шредингера принимает очень простую форму. Потенциальная энергия постоянна, так что и кинетическая энергия

W C eU D Wк

(192)

должна также оставаться постоянной. Если принять, что потенциальная энергия равна нулю, то W D Wк. Тогда

4		C	8 2m		W		D 0:	(193)
				h2
Для упрощения предположим, что				зависит только от одной координаты, например
от x. Тогда уравнение (193) перепишется в виде
d 2		C		8 2m			D 0:
						W		(194)
	dx2			h2

Это обычное одномерное волновое уравнение. Решение имеет вид:

		Ae˙j	2 p			W
			2 p			W
.x; t /	D		h	2mW x e	j 2	h	t :	(195)
	D

В это выражение введен зависящий от времени множитель. Если ввести длину волны, являющуюся мерой пространственной периодичности, используя формулу

	p		h		D	h	D ;	(196)

						p
						p
		2mW
то решение перепишется в виде
.x; t /			D	Ae˙j 2 x e j 2 t :				(197)
			D

Соотношения

D I W D h

позволяют ввести вместо импульса p и энергии W , т.е. величин, связанных с корпускулярными представлениями, величины, характеризующие волну, а именно длину волны и частоту. Заметим, что решения для движения в произвольном направлении имеют вид:

.x; y; z; t / D Ae˙j	2	.pErE˙W t / D Ae˙j	2	.px xCpy yCpz z/e j	2	W t :	(198)
	h		h		h

Подстановка (198) в уравнение (193) сразу же показывает, что (198) — действительно является его решением; при этом энергия W должна быть связана c величинами px , py , pz формулой вида

p		px2 C py2 C pz2 D 2mW D p2:	(199)
p

Величина 2mW , входящая в уравнение (195), носит название «импульс» и обозначается буквой p; это выражение получено из классических соотношений. В квантовой механике все, даже названия, необходимо заново обосновать; p будет выражать импульс лишь в том случае, если будет являться собственным значением оператора импульса. Решение (198) удовлетворяет уравнению Шредингера (193) для любой пары связанных друг с другом величин W и p. Это значит, что при свободном движении электрона ни энергия, ни импульс не квантуются (рис. 83).

137

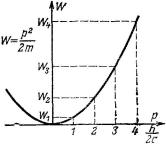
Рис. 83. В случае движения свободного электрона в неограниченном пространстве все значения импульса, а значит, и энергии разрешены: движение свободного электрона не квантуется. Но если электрон «заперт» в конечной (одномерной) области, то возможны лишь дискретные значения импульса и энергии (см. п. 2-4-3).

138

18Соотношение неопределенности Гейзенберга как решение уравнения Шредингера

Исследуем подробнее только что рассмотренный случай движения электрона в отсутствие поля в направлении оси x. Полученное решение имеет вид:

где =h/p — длина волны, являющаяся мерой периодичности в пространстве. Как известно, квадрат абсолютного значения .x; y; z/ выражает вероятность встретить электрон в единичном объеме около точки с заданными координатами x; y; z. Приведенная выше формула описывает направленный вдоль оси x бесконечно длинный луч волн с постоянной амплитудой; отсюда следует, что вероятность появления электрона для всех точек оси x имеет одно и то же значение. Таким образом, при заданных значениях W и p, а значит, при заданном значении ничего нельзя сказать о пространственном положении электрона. Волновой пакет, пространственная протяженность которого конечна, может быть составлен из волн с различной длиной волны. Подбирая соответствующим образом амплитуды и фазы, можно добиться того, чтобы эти волны всюду, за исключением очень малой области пространства, гасили бы друг друга. При этом решение уравнения

Шредингера представляется суммой членов вида e				j	2	.px W t /	с разными амплитудами

					h

C1
.x; t / D Z	A.p/ej	2	.px W t /dp:				(201)
		h
1

Отсюда следует, что если мы находим координаты электрона, то не можем наделять его определенным значением длины волны или импульса. И наоборот, если электрону приписывается определенный импульс, то его место в пространстве вообще можно не задавать. Пределы для одновременного задания импульса и положения частицы количественно определяются соотношением неопределенности Гейзенберга. Его получают на основании выражения (201). Пусть вероятность появления электрона в момент времени t D 0 для всех точек области от x D a=2 до x D Ca=2 постоянна, а всюду вне этой области равна нулю. Таким образом, в момент времени t D 0 должно выполняться условие

1				2		a		a
.x; 0/ D (	p		ej	h	p0 x при	2	< x <	2 I
		a							(202)

0при прочих x:

Содной стороны, оно удовлетворяет уравнению Шредингера, а кроме того, выпол-

няется равенство

CZa=2

dx	D	1	I	(203)

a=2

это значит, что электрон достоверно должен находиться в исследуемом интервале. Значение A.p/ можно рассчитать, используя интеграл Фурье.

Читателю, знакомому с основами техники связи, очевидно, известно представление сигнала f .t / интегралом Фурье

ZC1

f .t / D F.!/ej ! t d!

139

и его обращение

F.!/ D

f .t /e

j ! t dt:

Если произвести замену

t ! x;

! !

то эти уравнения можно, переписать в виде

p ej

f .x/ D Z

px dpI

p D

f .x/e j

px dx:

Введя теперь обозначения

f .x/ D .x; 0/I

p D A.p/;

получим выражение

.x; 0/ D Z A.p/ej

px dpI

A.p/ D

.x; 0/e j

px dx:

(204)

Согласно (202) для нашего случая запишем:

Ca=2

a=2

A.p/ D

h .p0 p/x dx D

j 2 p

.p0

ej h

.p0 p/a e

j h

.p0

p/a ;

(205)

или в более простом виде

A.p/ D

p/p

sin

.p0

p/:

(206)

.p0

Эта функция представлена на рис. 84. Рисунок доказывает, что импульсы, необходимые для образования волнового пакета, в основном приходятся на область от p0 C h=a до p0 h=a. Отсюда следует, что если неточность задания координаты местонахождения электрона в какой-то момент времени равна x D ˙a=2, то неточность импульса достигает значения p D ˙h=a. Следовательно, произведение неточностей

	x p		h
				:	(207)
			2

8Цуг волн — это модельное представление процесса излучения источника (атом					в воз-
бужденном состоянии) электромагнитных волн,		который колеблется в течение			некоторо-

го времени, излучая энергию в создание переменного электромагнитного поля. Источник: http://physics.spbstu.ru/forstudents/lectures/ivanov/opt1-8.pdf

140

а)

б)

Рис. 84. Чтобы образовать цуг8 волн длиной a, необходимо использовать значения импульсов, соответствующие интервалу p ˙h=a, лежащему около значения p0 (a). Понятие о микрочастице, движущейся по точно заданной траектории с заданной скоростью, в квантовой механике теряет смысл (б). Ввиду того, что роль частицы выполняет волновой пакет, траектория становится размытой.

Соотношение неопределенности Гейзенберга, таким образом, утверждает, что если неточность измерения координаты равна q, то эта величина и значение неточности определения соответствующего импульса p удовлетворяет неравенству

q p >	h	:	(208)
	4

Значение этого неравенства и в принципиальном, и в практическом отношении огром-

но.

Позднее будет показано, что подобное соотношение существует не только для неопределенности измерения координаты и импульса, но и для неопределенности измерения двух любых «канонически» сопряженных координат. Такими сопряженными координатами являются, например, энергия и время. Тогда понятию «неопределенность» будет дано более четкое толкование.

141

19Решение уравнения Шредингера для движения электрона в ограниченной части пространства

Дискретные значения энергии9 будут получаться в том случае, когда электрон, хотя и движется в пространстве, где силы не действуют, но это пространство ограниченно. Пусть электрон находится внутри прямоугольного параллелепипеда с ребрами a, b, c. Три грани параллелепипеда должны лежать в плоскостях xy, yz и zx. Целесообразно записать действительную часть решения:

			2		2
.x; y; z/ D A sin	2	px x sin			py y sin		pz z ;	(209)
	h			h		h

Так как вне параллелепипеда постоянна и равна нулю, то при x=0 и x D a независимо от y и z она должна принимать значение нуль. Однако это выполняется

только при условиях:
2		px a D n1 I	px D	n1 h	:	(210)

	h			2 a

Подобным же образом, записывая граничные условия для граней, перпендикулярных соответственно к осям y и z, запишем:

py D	n2 h				n3 h
			I	pz D		:	(211)
	2	b			2 c

В уравнениях (210) и (211) n1, n2 и n3 — любые целые числа. Отсюда, учитывая уравнение (199), можно получить:

	h2	n2			n2		n2	;
		1		2		3
Wn1 n2 n3 D				C		C			(212)
	2m		a2		b2		c2

другими словами, энергия может принимать лишь строго определенные дискретные значения (рис. 83).

В случае куба формула упрощается и принимает вид:

	h2	:
Wn1 n2 n3 D	8ma2 n12 C n22 C n32	:	(213)

Квантовые состояния, соответствующие числам n1, n2, n3, описываются функцией

x			y			z
n1 n2 n3 .x; y; z/ D A sin n1		sin n2			sin n3		:	(214)
	a			a		a

Обзор различных квантовых состояний или квантовых чисел, а также соответству-

ющих значений энергии значительно облегчается при помощи следующего построения. p

Изобразим три координатные оси и вдоль каждой оси нанесем величину h=.2a 2m/ в произвольном масштабе. Отметим узловые точки в пространстве согласно рис. 85. Тогда каждая точка будет отвечать определенному квантовому состоянию, в то время как квадрат расстояния каждой точки от начала координат дает значение соответствующей энергии. Это позволяет, например, легко ответить на вопрос, сколько возможных энер-

гетических уровней можно обнаружить в энергетическом интервале от W до W C d W . p

Определим сначала число энергетических состояний внутри сферы с радиусом r D W .

9Речь идет о наборе значений энергии, которыми в данном случае может обладать электрон

142


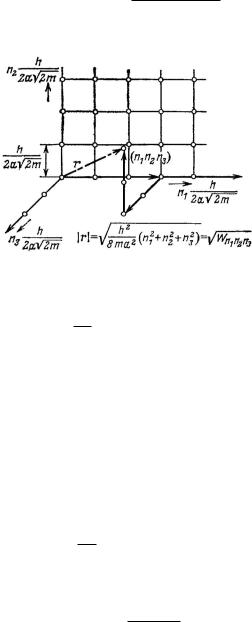
Это несложно: число энергетических состояний в сфере равно числу входящих в нее ма-
леньких кубиков с ребром h=.2ap		/, т.е.
леньких кубиков с ребром h=.2ap	2m	/, т.е.
N .W / D			4 r 3	1
					.h=2ap		/3	:	(215)
			3
			3			2m

Рис. 85. Возможные квантовые состояния и относящиеся к ним значения энергии электрона, заключенного в куб с ребром a.

Если учесть соотношения r D W и a3 D V , а также тот факт, что принимаются во внимание лишь положительные значения ni (отрицательные значения приводят к появлению знака минус у -функции, что не означает нового состояния) и, следовательно, надо рассматривать лишь 1/8 объема, то полученную формулу можно переписать в виде

N .W / D	4		.2mW /3=2
		V		:	(216)
	3		h3

Полученное выражение представляет число энергетических уровней, энергия которых меньше чем W . Число уровней в интервале от W до W C d W определяется формулой

4	V .2mW /1=2md W:
dN D h3	V .2mW /1=2md W:	(217)

Если сюда ввести импульс, определяемый уравнением (199), то получим:

dN D V	4 p2dp	:	(218)
	h3

Значение этого соотношения полностью выявляется при изучении квантовой статистики, где оно в сочетании с принципом Паули дает возможность судить о наибольшем числе электронов, которые могут разместиться в определенном энергетическом интервале.

143

20Решение уравнения Шредингера для туннельного эффекта

Выше рассматривались решения уравнения Шредингера для случая, когда силы не действуют, т.е. при постоянном значении потенциала. Обратимся теперь снова к решению одномерного уравнения Шредингера при условии, что потенциал, как показано на рис. 86, имеет постоянное значение на некотором отрезке. Частицы с зарядом q движутся слева направо. Зададимся вопросом, как ведут себя частицы при наличии потенциального барьера? Какая часть частиц проходит сквозь барьер, а какая часть отражается?

С классической точки зрения задача проста: если кинетическая энергия частиц больше высоты потенциального барьера, то они попадут в область справа от него; если же энергия меньше, то частицы независимо от ширины барьера всегда отражаются. Квантовая же механика приводит к совершенно иному решению.

Уравнение Шредингера описывает отдельно каждую из трех частей пространства. Разница заключается лишь в том, что сначала учитывается W , затем W qU , затем снова W . В соответствии с этим решения для трех частей пространства имеют вид:

j 2 p

D ACe

2mW

C A e

2mW

(219)

j 2 p

D BCe

2m.W qU /

C B e

2m.W qU /

(220)

j 2 p

D CCe

2mW

C C e

2mW

(221)

Рис. 86. Прохождение частицы сквозь потенциальный барьер.

Дальнейшая задача заключается в том, чтобы правильно, в соответствии с физическими условиями, выбрать коэффициенты A; B; C . Положительный знак экспоненты означает, что волна распространяется направо, отрицательный — налево. С уверенностью можно сказать, что в части пространства C могут находиться только те частицы, которые движутся вправо, в то время как в областях B и A могут находиться также и отраженные частицы, так что при решении необходим учет двух членов. Отсюда следует, что C =0.

Для определения остальных констант проведем следующее рассуждение. В уравнение Шредингера входит потенциал U , а также вторая производная от , т.е. 00. Если потенциал меняется скачкообразно, то, следовательно, в данном месте и вторая производная от тоже должна измениться скачкообразно, а это значит, что первая производная имеет точку перегиба, являясь при этом, как и сама функция , непрерывной. Таким образом, необходимо, чтобы решения, написанные для частей пространства A; B и C , а также их первые производные непрерывно смыкались в точках x D 0 и x D l . Запишем:

A D B I	d A	D	d B	; когда x D 0;	(222)
	dx		dx

144

B D C I	d B	D	d C	; когда x D l:	(223)
	dx		dx

Если эти уравнения записать подробно, то нетрудно получить:

AC C A

D BC C B I

(224)

A / D p

а также

.AC

qU /.BC

B /;

(225)

j 2 p

BCe

2m.W

qU /l

C B e

2m.W qU /

D CCe

2mW

(226)

j 2 p

qU BCe

2m.W qU /

B e

2m.W qU /

(227)

p2mW l

j h

W CCe

В нашем примере AC выражает амплитуду волны, падающей на потенциальный барьер; CC — амплитуду волны, просочившейся через барьер и идущей дальше. В первую очередь нас интересует, какая часть от падающих частиц проникает сквозь барьер. Определим для этого отношение CC=AC. Разделим каждый член уравнений системы (224), (225), (226) и (227) на AC и введем для упрощения обозначения

k12 D	8m 2		k22 D	8m 2
		W I			.W qU /:	(228)
	h2			h2

В результате получается система уравнений вида

1 C

k1 1

D k2 AC

AC I

j k2 l

j k1 l

j k2 l

D k1

j k1 l

Это неоднородная линейная система уравнений с четырьмя неизвестными:

	A		BC		B		CC
	AC	I	AC	I	AC	I	AC	;

которая решается без принципиальных трудностей. Так, используя последнюю пару уравнений, можно величины BC=AC и B =AC выразить через CC=AC. Подстановка этих величин в первые два уравнения дает два уравнения с неизвестными A =AC и CC=AC. Решая их, можно получить выражение

	C		j k1 l	ch kl C j	k2 k2	sh kl ;
1 D	C				1
	AC	e			2k1k		(229)

откуда находится значение CC=AC; здесь величина k введена равенством j k D k2, и в интересующем нас случае qU > W является действительным числом.

145

Результат показывает, что для частиц существует конечная вероятность проникнуть сквозь потенциальный барьер:

C	C	C	C		4k	2k2		:
				D		1
AC		AC			.k2 C k12/2 ch2 kl .k2		k12	/2

Введем теперь упрощающее предположение. Пусть kl велико по сравнению с единицей. Тогда

ch kl	D	ekl C e kl	ekl		:
		2		2

Совершенно ясно, что это число очень большое, следовательно, второй член в знаменателе можно не учитывать. Заменяя в полученной формуле введенные ранее для упрощения обозначения соответствующими им величинами, получаем окончательно:

16W .qU

W /

4 l

p2mpqU W :

(230)

.qU /2

На основании этого равенства можно сделать следующее заключение. Ранее предполагалось, что qU > W , т. е. высота потенциального барьера больше, чем кинетическая энергия частицы. С классической точки зрения в этом случае частица не могла бы преодолеть потенциальный барьер. Квантовая же механика утверждает, что есть конечная вероятность того, что частица, несмотря на указанное условие, может оказаться на противоположной стороне классически непреодолимого потенциального барьера: частица как бы прокладывает туннель. Этим и было вызвано появление термина «туннельный эффект». Понятно, что это выражение является лишь образом, в котором не следует искать глубокого смысла и которое совершенно не является объяснением явления (рис. 87). Вероятность проникновения тем больше, чем уже потенциальный барьер и чем меньше различие между энергией частицы и высотой барьера. В случае очень широкого барьера для частицы не существует сколько-нибудь заметной вероятности проникновения и с точки зрения квантовой механики. Необходимо добавить, что если энергия частицы больше высоты потенциального барьера, то и в этом случае имеют место отклонения от классических законов: с классической точки зрения в этом случае все частицы проходят через потенциальный барьер, в то время как квантовая механика показывает, что будут наблюдаться и отраженные частицы.

Рис. 87. Туннельный эффект наиболее наглядно можно представить как прохождение волны через абсорбирующий слой конечной толщины.

Туннельный эффект играет важную роль в теории радиоактивного распада, а также в представляющем для нас большой интерес количественном описании автоэлектронной эмиссии металлов.

146

21Решение для пространственной части уравнения Шредингера для атома водорода

Детальное описание параметров атома водорода с технической точки зрения не представляет особого интереса. Однако тот факт, что невзирая на это данный вопрос все же будет здесь рассмотрен, имеет две причины.

С физической точки зрения атом водорода как простейшая, но не тривиальная микросистема является пробным камнем каждой новой теории. В этом случае полностью раскрывается возможность метода квантования. С другой стороны, в дальнейшем на это детальное рассмотрение мы будем опираться в тех случаях, когда будут приведены лишь конечные результаты решения квантовомеханической задачи, описывающей то или иное явление. Можно представить, насколько сложен необходимый математический аппарат в случае рассмотрения более сложных явлений, если решение даже этой простейшей задачи столь трудоемко математически.

Тот факт, что стационарные волновые процессы при заданных условиях могут проявляться лишь в совершенно определенных характерных формах, известен, как это уже упоминалось, и в классической физике. Хорошо известны дискретные состояния, наблюдающиеся при колебаниях струны, закрепленной на обоих концах. Математически это выражается в том, что волновое уравнение струны имеет решение, дающее амплитуду, равную нулю в точках закрепления, лишь при определенных значениях частоты. Таким образом, метод квантования, используемый в волновой механике, значительно ближе к классической физике, чем к боровскому квантованию. С совершенно аналогичным появлением дискретных значений энергии мы уже встречались при рассмотрении состояний электрона, заключенного в замкнутом объеме.

В задаче об атоме водорода, прежде всего, следует показать, как именно отыскание решения, которое имело бы конечное значение на конечном интервале и превращалось бы в нуль на бесконечности, приводит к появлению дискретных энергетических состояний.

Исходя из представлений об атоме водорода, найдем энергетический уровень водородоподобной системы, состоящей из одного электрона, обращающегося вокруг любого ядра с зарядом Ze. В этом случае потенциальная энергия, подставляемая в уравнение Шредингера, выражается формулой


	qU D			Ze2
						:		(231)
				4 "0r
Уравнение Шредингера записывается в виде
	2m	W C			Ze2
4 C	8						D 0:	(232)
	h2				4 "0r
Нужно определить из этого уравнения			. Так как силовое поле обладает сферической

симметрией, то целесообразен переход к сферическим координатам r , # , '. Тогда потребуется найти функцию .r; #; '/. Прежде всего, следует переписать оператор Лапласа

@x2

@y2

@z2

в сферических координатах:

1 @

4 D

r 2

sin #

(233)

r 2

r 2 sin #

r 2 sin2 #

@'2

147

Уравнение Шредингера, следовательно, будет иметь вид:

1 @

1 @2

r 2

sin #

r 2 @r

r 2 sin #

r 2 sin2 #

@'2

(234)

W C

4 "0r

D 0:

8 2m

Ze2

Для решения дифференциального уравнения такого типа используется метод разделения переменных. Функцию .r; #; '/ перепишем в виде произведения функций, из

которых одна зависит лишь от r , а вторая от # и ':
.r; #; '/ D R.r /Y .#; '/ D RY:	(235)

Если учесть, что при дифференцировании по r можно считать постоянной функцию Y , а при дифференцировании по # и ' — функцию R, то уравнение (234) можно переписать:

1 @

R @

R @2Y

r 2

sin

r 2

r 2 sin #

r 2 sin2 #

@'2

(236)

8 2m

W C

Ze2

RY D 0:

4 "0r

После умножения уравнения на r 2=RY и разделения переменных получаем:

1 @

8 2m

Ze2

r 2

r 2 W C

R @r

4 "0r

@2Y

sin #

sin2 #

@'2

В левую часть этого уравнения входят величины, зависящие только от r , а в правую часть — величины, зависящие от # и '. Равенство этих двух частей возможно лишь в том случае, если они обе равны одной и той же постоянной величине:

1 d

8 2m

W C

Ze2

r 2

D I

(237)

4 "0r

1 @

@2Y

D :

sin #

(238)

sin #

sin2 #

@'2

Введенную постоянную называют параметром разделения. Разделив эти уравнения, их можно записать в виде

1 d

W C

Ze2

R D 0I

r 2

(239)

r 2 dr

4 "0r

r 2

1 @

@2Y

sin #

C Y D 0:

(240)

sin # @#

sin2 #

@'2

Используя подстановку

Y .#; '/ D .#/˚.'/;

148

можно произвести дальнейшее разделение последнего уравнения. Для этого подставим написанное выражение в уравнение (240), после чего полученное равенство умножим на sin2 #= ˚ , тогда получим:

1	sin #	@	sin #	@	C	1 @2˚	C sin2 # D 0:

		@#		@#		˚ @'2

Это уравнение распадается на два уравнения:


				1 d 2˚
							D m2;
				˚	d'2		D m2;
1	sin #	d	sin #			d		C sin2 # D m2:

		d#				d#

Решение можно сразу задать в виде

˚ D Aej m' :

Условие однозначности требует, чтобы m принимало значение

m D 0; ˙1; ˙2; : : :

так как только в этом случае ˚ принимает одинаковые значения для ' и ' C 2 .

Для нахождения решения второго уравнения несколько видоизменим его:

sin #

D 0:

sin # d#

sin2 #

Введя новую переменную

x D cos # I

dx D

sin # d#

и произведя замену ! y, получим дифференциальное уравнение вида

y D 0:

(241)

1 x2

Если сначала выбрать значение m D 0, то мы получим хорошо известное уравнение

Лежандра:

1 x2

C y D 0

или

1 x2

d 2y

C y D 0:

dx2

В качестве пробного решения

обычно записывается степенной ряд

ar xr I a0 ¤ 0:

y D xp

r D0

Подставив это решение в уравнение, получим выражения для коэффициентов при одинаковых степенях x, каждый из которых должен равняться нулю. Самая низкая степень будет у члена, содержащего xp 2. Выражение соответствующего коэффициента имеет вид:

a0p.p 1/ D 0 ! p D 0 или p D 1:

149

Для коэффициента при xp 1 справедливо выражение

a1.p C 1/p D 0:

Если выбрать p D 0, то второму уравнению удовлетворяет любое значение a1. Таким образом, в решение войдут две произвольные постоянные и мы получим фундаментальную систему. Можно написать:

y D a0 C a1x C a2x2 C : : : ; a0 ¤ 0:

Выразим теперь коэффициент при xr :
ar C2.r C 2/.r C 1/		ar r .r 1/					2ar r C ar D 0;
или		r .r C 1/
a	r C2 D							a	:
a								a	:
		.r	C	2/.r	C	1/ r
			C		C

Чтобы судить о сходимости, исследуем эти коэффициенты для случая r ! 1. Полу-

чим:	ar C2		r
		D		;
	ar		r C 2

откуда следует, что коэффициенты стремятся к нулю как члены гармонического ряда. Так как x в соответствии с формулой x D cos # принимает значения, лежащие в интервале 1 6 x 6 C1, то при x D C1 .# D 0/ степенной ряд, так же как и гармонический, расходится. Решение без особых точек во всей области мы получим лишь в том случае, если сумма останется конечной; следовательно, при некотором заданном r D l ряд

должен быть оборван. Это имеет место, когда

D l.l C 1/:

(242)

Тогда мы получаем полином l -й степени. Такие полиномы носят название полиномов

Лежандра. Некоторые из них приведены ниже:

.3x2

.5x3

P0.x/ D 1I P1.x/ D xI

P2.x/ D

1/I

P3.x/ D

3x/:

Если теперь произвести jmj-кратное дифференцирование уравнения

.1 x2/

d 2Pl .x/

dPl .x/

C l.l C 1/Pl .x/ D 0;

dx2

то получим новое уравнение:

2P .jmj/

dP .jmj/

.1 x

2x.jmj C 1/

C hl.l C

1/ j

mj.jmj C 1/iPl j

D 0; (243)

dx2

где

d jmjPl .x/

Pl.jmj/ D

dxjmj

Уравнение (243) наиболее просто выводится методом математической индукции. Если с помощью формулы

Plm.x/ D .1 x2	jmj
	/ 2 Pl.jmj/.x/:

150

ввести определение сопряженного полинома Лежандра P m.x/, то получим для него
								l
уравнение
	d 2P m.x/		dP m.x/					m2
	l		l						m
1 x2		2x		C l.l C 1/					Pl	.x/ D 0:
1 x2	dx2	2x	dx	C l.l C 1/			1 x2		Pl	.x/ D 0:
Тогда решение уравнения (241) запишется в виде
	Plm.x/ D 1 x2				jmj d jmjPl .x/
					2			;
						dxjmj		;

где jmj 6 l ; во всех прочих случаях при дифференцировании получается нуль.

151

22Решение для угловой части уравнения Шредингера для атома водорода

Для Y .#; '/ получим теперь выражение
Ylm.#; '/ D ej m' Plm.cos # /; m D 0; ˙1; ˙2; : : : ; jmj 6 l:	(244)

Если в уравнение (239) подставить выражение (242) для и провести дифференцирование, то можно записать:

d 2R

2 dR

8 2mW

8 2mZe2

l.l C 1/

(245)

C r dr

4 "0r h2

dr 2

r h2

Используем для сокращения записи подстановку:

8 2mW

8 2mZe2

D 2˛:

4 "0h2

Тогда уравнение перепишется в виде

C r

dr 2 C r dr

r02

r 2

d 2R

2 dR

2˛

l.l

C 1/

(246)

Вводя с помощью выражения

D 2 r r0

новую независимую переменную, получим:

d 2

C d

4 C

d 2R

2 dR

˛r

l.l

C 1/

(247)

так что в случае ! 1 уравнение примет очень простую форму

d 2R

R D 0:

d 2

Решение этого уравнения имеет вид R. /

D e

(решение, имеющее знак плюс,

расходится на бесконечности и поэтому отбрасывается). Таким образом, целесообразно искать решение в форме


R. / D e 2 f . /:	(248)

Если это выражение подставить в уравнение (247), то получится новое дифференци-

альное уравнение для f . /:

d C

d 2

d 2f

.˛r

l.l C 1/

(249)

Для решения этого уравнения образуем степенной ряд

f . / D s .a0 C a1 C a2 2 C : : :/ D s

a0 ¤ 0:

a ;

(250)

152

Это выражение подставляется в дифференциальное уравнение, после чего можно привести подобные члены. Если f . / действительно является решением, то все коэффициенты должны быть равны нулю. Самая низкая степень здесь равна .s 2/. Равенство нулю соответствующего коэффициента выражается равенством

a0Œs.s 1/ C 2s l.l C 1/ D a0Œs.s C 1/ l.l C 1/ D 0:

(251)

В общем виде коэффициент, соответствующий степени Cs 1, записывается в виде

Œ. C s C 1/. C s/ C 2. C s C 1/ l.l C 1/ a C1 . C s C 1 ˛r0/a D 0: (252)

Первое из этих двух уравнений дает, что s D l или s D .l C 1/. Последнее значение приводит к бесконечно большому f . / при D 0. Значит, остается одно возможное значение s D l . Тогда из второго равенства следует, что


	a C1		D			C l C 1 ˛r0	:	(253)
	a			. C l C 1/. C l / C 2. C l C 1/ l.l C 1/

Если ! 1, то		a C1		D	1	. Это указывает на экспоненциальное возрастание f . /.
		a

Если потребовать, чтобы функция e =2f . / также сохраняла на бесконечности конечное значение, то следует из бесконечного ряда получить полином конечной степени. Ряд оборвется на -м члене и a C1 превратится в нуль, если

C l C 1 ˛r0 D 0I C l C 1 D ˛r0:

(254)

Подстановка сюда значений ˛ и r0 с неизбежностью дает для конечного решения выражение

W D		mZ2e4
					; ; l D 0; 1; 2; : : :	(255)
		8"02h2. C l C 1/2
Далее вводится главное квантовое число n D C l C 1 D ˛r0. Тогда
	W D		mZ2e4
				; n D 1; 2; 3; : : :		(256)
			8"02h2n2

Если Z D 1, то получим известную формулу Бальмера. Из равенства n D C l C 1 следует, что l может принимать при заданном n значения

l D 0; 1; 2; : : : ; n 1:

Таким образом, мы получили дискретные значения энергии.

Как мы уже убедились, определение условий однозначности и конечности функции в большинстве случаев ведет к решению основной задачи, т.е. к получению дискретных значений энергии системы. Для полноты описания приведем функцию в явной форме. Решение уравнения (247) имеет вид

							r
R. /	D	e	2 l L2l C1	. /;	D	2		:	(257)

			nCl			r0

Входящий сюда полином L2lnCCl1. /, коэффициенты которого определяются уравнениями (251) — (252), является сопряженным полиномом Лагерра. Полином Лагерра i -го порядка является решением уравнения

xy00 C .1 x/y0 C iy D 0; i D 0; 1; 2; : : :

(258)

153

и записывается в виде

	i
Li .x/ D	X	.	1/k	Cki xk :	(259)
		.	1/k
	kD0		k!
	kD0

Если присоединенные полиномы Лагерра выразить в виде

Lip	d p
Lip	.x/ D dxp Li .x/;	(260)

то, произведя p-кратное дифференцирование уравнения (258), можно убедиться, что (260) удовлетворяет уравнению

xy00 C .p C 1 x/y0 C .i p/y D 0

(261)

Сравнивая (261) с уравнением, получаемым из (249) путем подстановки функций вида f . / D L. /, а именно

d 2L		C .2l C 2	/	dL		C .˛r0	l 1/L D 0;
								(262)
	d 2				d

Таблица 2. Состояния системы с одним электроном при самых низких значениях энергии.

Отдельные состояния обозначены цифрами, соответствующими главному квантовому числу, и буквами, соответствующими написанному рядом побочному (азимутальному) квантовому числу; l D 0 соответствует s-состоянию, l D 1 — p-состоянию электрона.

Обозначение

состояния

r 3

2 e

2r1

j '

-1

2r1

sin # e

e 2r1 cos #

2 r

2r1

sin # ej '

и учитывая, что

D r0

˛ D

n, найдем, что решение, записанное выражением (257),

действительно может содержать L

nCl

.2l

n l 1.

C . /. Это полином степени n

Отсюда следует, что l может принимать значения l D 0; 1; 2; 3; : : : ; n

Решение, характеризуемое тремя квантовыми числами n, l , m, таким образом, может быть записано в виде

		2r	l		2r
nl m.r; #; '/ D Ae	r		Ln2lCCl	1		Pim.cos #/ej m' :
	nr1						(263)
		nr1			nr1

Здесь A — нормирующий множитель, a диусу первой боровской орбиты:

2r 2r ˛ 1 r0˛ D nI D r0 D n I ˛

r1 идентичен уже встречавшемуся ранее ра-

	"0h2		r1H		a0
D r1 D		D		D		:	(264)
	mZe2		Z		Z

154

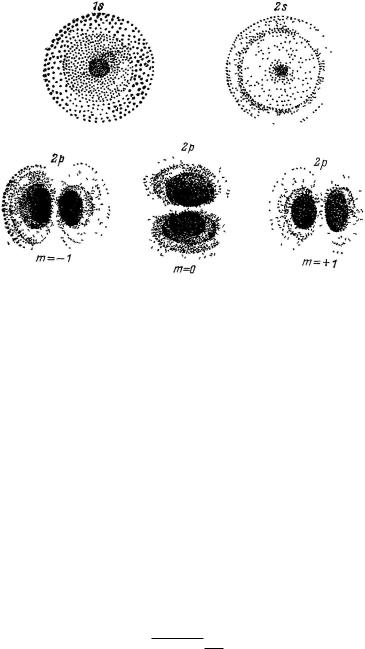
Возникает вопрос, сколько различных решений соответствует заданному значению n. Известно, что l может принимать значения от 0 до n 1. Число m (при заданном l ) может принимать всего 2l C 1 значение от — l до Cl . Отсюда следует, что общее число решений равно:

Xn 1

.2l C 1/ D n2:

(265)

l D0

В табл. 2 приведены -функции с рассчитанным нормировочным множителем, отно-

сящиеся к наиболее низким квантовым числам. На рис. 88 представлены значения
для нескольких решений.

Рис. 88. Распределение вероятности распределения единичных векторов, характеризующих положение электрона в пространстве в некоторых, наиболее низких энергетических состояниях системы. Состояния 1s и 2s обладают сферической симметрией.

Выше уже было показано, что данному n соответствует точно n2 различных функций. Другими словами, одному значению энергии соответствует n2 разных функции . В подобном случае говорят, что данное состояние вырождено с кратностью вырождения n2. Так же как и в случае теории Бора, это вырождение может быть снято любым малым возмущением. Одно значение энергии расщепляется на n2 различных значений. Если атом помещается в магнитное поле, то имеет место нормальный эффект Зеемана, энергетические уровни при этом смещаются, причем, как мы в этом убедимся позже, в соответствии с теорией Бора. Ниже будет также показано, что в этом смещении играет определяющую роль квантовое число m, которое до сих пор имело лишь математическое значение, именно это оправдывает его отождествление с магнитным квантовым числом. Точно так же становится понятной связь квантового числа l с орбитальным моментом. Однако для орбитального момента, как будет показано далее, вместо значения l h=2 получается находящееся в согласии с опытом значение

pl.l C 1/ 2h ;

уже не раз приводившееся выше.

Квантовая механика автоматически без какого-либо искусственного предположения привела к дискретности значений энергии; точно так же были получены ограничения,

155

связанные с квантовыми числами и получаемыми экспериментально значениями моментов количества движения. Однако все это было получено ценой абсолютной потери наглядности, понимаемой в классическом или в повседневном смысле. Следует заметить, что квантовая механика не привела к представлению о собственно механическом и магнитном моментах электрона. Эти величины, согласующиеся с опытом, могут быть получены только лишь в рамках релятивистской квантовой механики, на основании уравнений Дирака. Подробно этим вопросом мы заниматься не будем. Возвратимся к предложенному Паули математическому описанию спина. Для начала ограничимся основанным на опыте утверждением, что электрон обладает собственным механическим и магнитным моментами и что для описания электронного состояния необходимо указы-

вать и спиновое квантовое число

s D ˙ 12 :

Понятно, что теперь -функция нуждается в поправке; трем числам n, l , m соответствует

пара функций
				1
C 12	D	nl m.r; #; '/	s C			I
					2
2	D	nl m.r; #; '/	s	1
				2 :
1
Природа спиновой функции	s	глубоко не изучена. Следует только заметить, что

полная функция состояния зависит не только от пространственных, но и от спиновых координат. В соответствии с этим энергии Wn соответствует не n2, а 2n2 различных функций, т.е. она осуществляется посредством 2n2 разных квантовых состояний.

156

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2517 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.04.201543.01 Кб37конспект Евгения Онегина.doc
#
16.04.2019104.82 Кб1конспект замула.docx
#
20.11.201827.99 Кб0конспект исправ.docx
#
22.05.20152.48 Mб357КОНСПЕКТ К СЕМИНАРАМ.doc
#
21.09.201929.33 Кб1конспект КиЭС, 2ая часть.docx
#
21.03.201610.86 Mб75Конспект Клемешева.pdf
#
10.08.201933.15 Mб5Конспект лаборабораторных работ ИТвЭ.doc
#
15.04.2015564.22 Кб64Конспект лекций по курсу Введение в биологию1.doc
#
09.11.2018351.74 Кб3Конспект лекций по курсу Введение в биологию1.doc
#
14.04.2019346.62 Кб3Конспект лекций по курсу Введение в биологию1.doc
#
12.11.2018883.71 Кб17Конспект лекций по мат. моделированию.doc