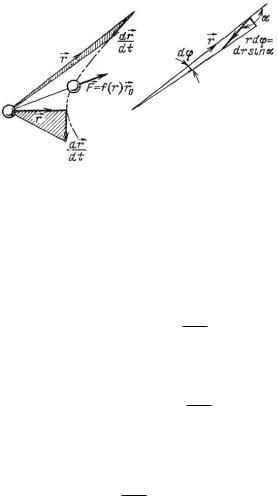
6Движение частиц в поле центральных сил. Форма траектории. Рассеяние ˛-частиц атомными ядрами. Дви-

жение электрона в поле атомного ядра.

6.1Общие следствия из уравнения движения

Простейшее электрическое поле создается неподвижным точечным зарядом, например ядром атома. Вообще центральными называют все силовые поля, в которых сила в любой точке является функцией расстояния от неподвижной точки — центра, а направление силы совпадает с линией, соединяющей эти две точки. Следовательно,

E D E

F f .r /r0;

где r — расстояние точки от центра, а rE0 — единичный вектор, направленный от центра к рассматриваемой точке. Например, сила, действующая на электрон в поле ядра атома с зарядом Ze , выражается формулой

Рис. 21. Иллюстрация, поясняющая закон площадей. Предполагается, что знак заряда у обеих частиц одинаков.

Отрицательный знак здесь означает, что сила направлена к центру.

Закон площадей справедлив и в общем случае центральных полей (рис. 21). Уравнение движения гласит:

Умножая векторно обе части уравнения на rE, получаем:

Так как rE и rE0 параллельны, их векторное произведение равно нулю, то:

rE d 2rE D 0 dt 2

30

Векторное произведение d rE=dt на само себя равно нулю. Таким образом, справедливо

где aE — константа. Величина, стоящая в левой части уравнения, равна удвоенной площади, прочерченной радиус-вектором за единицу времени. То, что она постоянна, известно из законов движения планет. Постоянная величина, стоящая в правой части уравнения, обозначена 2aE, потому что aE здесь выражает секториальную скорость. Отсюда следует, что частица движется в плоскости. Поэтому в последующем имеет смысл использовать полярные координаты r; ':

Тогда второй закон Кеплера можно записать в форме (рис. 21)

Если теперь исследовать орбиту частицы с зарядом Z1e в поле другой частицы с зарядом Z2e, предполагаемой неподвижной, то необходимо записать лишь закон сохранения

где левая часть отнесена к любой точке P траектории, а правая соответствует точке траектории, выбранной за исходную.

6.2 Форма траектории

Таким образом, мы выразим 'P и rP через величины, характеризующие траекторию. Для v2 можно получить:

31

Закон сохранения энергии теперь принимает вид:

Это уравнение уже является дифференциальным уравнением траектории, которое после разделения переменных перепишется в форме

Интегрирование уравнения не вызывает трудностей. Вводя переменную x D 1=r , получаем для правой части:

Интеграл от этого выражения представляет собой арккосинус некоторой функции:

Таким образом, мы установили вид функции ' D '.r / и затем найдем выражение r D r .'/

где значения g и понятны без дальнейших пояснений. Само уравнение, как известно, является уравнением конического сечения, а именно, в зависимости от уравнением

эллипса, параболы или гиперболы; кривая является при < 1 — эллипсом,

при D 1 — параболой,

при > 1 — гиперболой.

Подробное исследование вышеприведенной зависимости интересно в двух случаях. Один из них — это движение электрона с зарядом e в поле положительного ядра с зарядом Ze. Второй — поведение заряженных ядер гелия с зарядом C2e; т. е. ˛-частиц, в поле ядра с зарядом CZe. В первом случае движение может происходить по любому коническому сечению, а во втором — только по гиперболе.

Рассмотрим сначала второй случай.

6.3Рассеяние ˛-частиц атомными ядрами

Исследуем следующий случай. Ядра гелия с зарядом C2e; скоростью v0 и массой m влетают в поле атомного ядра, имеющего массу M m и заряд Ze. Нас интересует вид траектории первой частицы. На этот вопрос в предыдущем разделе ответ уже был дан. Траектория будет гиперболой. Сосредоточим внимание теперь на вопросе, как

32

велико отклонение частицы в поле ядра, т.е. как велик угол # . В случае одинаковых ионов с одинаковой энергией этот угол будет зависеть лишь от расстояния p, называемого параметром удара («impact» параметр). Очевидно отклонение будет большим при малом расстоянии, и наоборот. Легко получить количественные соотношения. Уравнение траектории получаем на основании формулы (10):

В точке, бесконечно удаленной, известен момент импульса v0p для траектории. Эта

Здесь учтено, что скорость принимает значение v0 в точке r D r0; а в нашем случае r0 D 1, следовательно, 1=r0 D 0: Эксцентриситет выражается в виде формулы

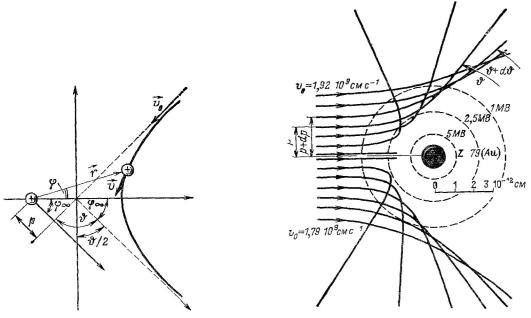
Это позволяет непосредственно по рис. 22,а найти соотношение для угла отклонения:

Путем простой подстановки можно получить отсюда конечную формулу:

Формула (12) показывает, что отклонение тем меньше, чем больше параметр соударения.

Приведенное выше соотношение нельзя доказать экспериментально, так как величина p, играющая здесь основную роль, не может быть непосредственно измерена. В действительности изучается, естественно, не рассеяние одного атомного ядра на другом,

33

а рассеяние пучка частиц, например ˛-частиц, направляемого на тонкую фольгу. При этом исследуется, сколько частиц отклоняется в каждом направлении. Если обозначить толщину фольги t , а число частиц в единице объема N , то в объеме фольги, приходящемся на единицу ее поверхности, находится N t центров рассеяния. Предполагается, что эти центры удалены достаточно далеко один от другого, так что их поля не влияют друг на друга. Кроме того, будем считать, что падающая частица рассеивается только одним ядром. Нарисуем теперь кольцо с внутренним радиусом p и внешним — p C dp вокруг каждого центра рассеяния. Частица, первоначально двигавшаяся внутри этого кольца, затем рассеивается в пределах области, заключенной между двумя коническими поверхностями, определяемыми углами # и # C d# . Согласно уравнению (12) p и # связаны друг с другом формулой

Рис. 22. Движение заряженной частицы в поле другой неподвижной заряженной частицы (а) и рассеяние ˛-частиц с энергией 7.97 и 6.77 МэВ, возникающих при распаде Тh, на ядре золота

(б). Пунктирные линии изображают эквипотенциальные поверхности (по Блатту-Вейскопфу).

Если на единицу поверхности за единицу времени падает n первичных частиц, то число частиц, попавших в цилиндрические кольца, окружающие N t центров, будет равно:

d n D nN t 2 pdp:

Понятно, что все эти частицы будут отклоняться в области, определяемые углами # и # C d# . Так мы приходим, наконец, к формуле Резерфорда

34