9.3. Визначення помилки і необхідної чисельності серійної вибірки

Методичні вказівки

При серійній вибірці генеральну сукупність ділять на однакові за об'ємом групи - серії. У вибіркову сукупність відбираються серії. Усередині серій виробляється суцільне спостереження одиниць, що попали в серію. Середня помилка серійної вибірки при без повторному відборі серій визначається по формулі:

,

(9.19)

де - між серійна дисперсія середніх (долі);

R - число серій в генеральній сукупності;

r - число вибраних серій.

Порядок визначення граничної помилки серійної вибірки (), меж, в яких знаходяться значення генеральної середньої () і генеральної долі (р) представлений в п. 9.1.

Необхідна чисельність серійної вибірки визначається по формулі:

.

(9.19)

Задачі

9.13. Для встановлення середнього терміну служби деталей з сукупності, що включає 1000 шт., касет з деталями, методом механічного відбору перевірено 10 касет. Результати перевірки показали, що середній термін служби деталей у відібраних касетах склав (місяців): 7; 8.2; 8.6; 7.2; 8.0; 5.8; 8.8; 7.2; 6.1; 6.0. Середній термін служби деталей у вибірці - 7.6 місяця. З вірогідністю 0.997 визначите межі, в яких знаходиться середній термін служби деталей у всій сукупності.

9.14. З партії насіння, розбитої на 40 рівних по величині серій, методом випадкового без повторного відбору було перевірено 8 серій на схожість. В результаті обстеження встановлено, що доля насіння, що зійшло, складає 75%. Між серійна дисперсія дорівнює 900. З вірогідністю 0.683 визначите межі, в яких знаходиться доля схожості насіння у всій партії.

9.15. На склад заводу поступило 100 ящиків готових виробів по 80 шт. в кожному. Для встановлення середньої ваги деталей необхідно провести серійну вибірку деталей методом механічного відбору так, щоб з вірогідністю 0.954 помилка вибірки не перевищувала 2 грами. На основі попередніх обстежень відомо, що дисперсія серійної вибірки дорівнює 4.

9.16. На заводі, що має 200 бригад, проектується серійна вибірка для встановлення долі робітників заводу, що виконують норму виробітки. Потрібно визначити необхідну чисельність вибірки, аби з вірогідністю 0.954 гранична помилка вибірки не перевищувала 5%, якщо між серійна дисперсія долі дорівнює 225.

Тема 10. Графічний метод

Практичні заняття по темі передбачають вирішення наступних типів задач: 1) графіки рядів розподілу; 2) графіки динаміки.

10.1. Графіки рядів розподілу

Методичні вказівки

Основна мета графічного зображення розподілу полягає в тому, аби дати наочне уявлення про структуру сукупності, характер і форму розподілу статистичної сукупності, структурні зрушення.

Для побудови графіків розподілу використовують, як правило, прямокутну систему координат. При цьому на осі абсцис відкладають значення вар’їручої ознаки, а на осі ординат - відповідні частоти.

Найчастіше ряди розподілу зображаються у вигляді діаграм - стовпчикових, стрічкових, секторних.

Варіаційні ряди зображують у вигляді гістограми, полігону, кумуляти і огіви.

Гістограма розподілу будується в прямокутній системі координат. На осі абсцис відкладають відрізки, пропорційні інтервалам варіаційного ряду, і на кожному з них, як на фундаменті, в прийнятому масштабі будують прямокутник, висота якого пропорційна частоті даного інтервалу.

Полігон. По осі абсцис відзначають точки, відповідні значенням середин інтервалів, і з них проводять перпендикуляри, на яких відкладають по осі ординат відрізки, пропорційні частотам варіантів. Полігони застосовують головним чином для зображення дискретних варіаційних рядів, але вони можуть бути застосовані і для зображення інтервальних рядів.

Кумулятивна крива (кумулята) - зображення в прямокутній системі координат варіаційного ряду з накопиченими частотами. По осі ординат відкладають відрізки, довжини яких пропорційні накопиченим частотам варіантів дискретного ряду і через них проводять лінії паралельні осі абсцис, а по осі абсцис відзначають точки, відповідні значенням варіантів ознаки, і з них проводять перпендикуляри до пересічення з відповідними горизонтальними лініями. Якщо провести через ці точки пересічення прямі лінії, то вийде ламана крива - кумулята.

У кумуляти інтервального варіаційного ряду нижній межі першого інтервалу відповідатиме частота або частість, рівна нулю, а верхній межі - частота першого інтервалу; верхній межі другого інтервалу відповідає накопичена частота перших двох інтервалів і так далі. Верхній межі останнього інтервалу відповідає сума всіх частот ряду.

Якщо по осі ординат відкладати значення ознаки, а по осі абсцис накопичені частоти і з'єднати вершини абсцис прямими лініями, то отримаємо ламану криву - огіву.

Завдання

10.1. Є наступні дані про розподіл випускників вищих учбових закладів регіону по формах навчання в 2006 році:

Форма навчання	Кількість випускників, тис. чол.	Питома вага у відсотках до підсумку, %
Стаціонар	73.3	53.5
Вечірня	11.7	8.6
Заочна	51.9	37.9
Разом	136.9	100

Представте дані розподілу у вигляді: 1) одно-стовпчикової діаграми; 2) одно-стрічкової діаграми.

10.2. Представте розподіл, наведений в попередньому завданні, у вигляді: 1) багато-стовпчикової діаграми; 2) багато-стрічкової діаграми.

10.3. Є наступні дані про розподіл випускників вищих навчальних закладів різного рівня акредитації по формах навчання у 2006 г:

Форма навчання	Кількість випускників ВНЗ, тис. чол.
	ВНЗ III–IVрівня акредитації	ВНЗ I–II рівня акредитації
Стаціонар	73.3	43.9
Вечірня	11.7	-
Заочна	51.9	20.5
Разом	136.9	64.4

Відтворіть представлені дані у вигляді серійно-стрічкової діаграми.

10.4. Відтворіть розподіл, представлений в попередньому завданні, у вигляді секторних діаграм.

10.5. Є наступні дані про розподіл заводів цементної промисловості за розміром основних виробничих фондів:

Групи завів за розміром основних фондів, млн. грн.	Число заводів у відсотках до підсумку, %
1-3	4.6
3-5	13.6
5-7	15.9
7-9	52.3
9-11	13.6
Разом	100

Представте дані розподілу у вигляді: 1) гістограми;. 2) полігону; 3) кумуляти; 4) огіви.
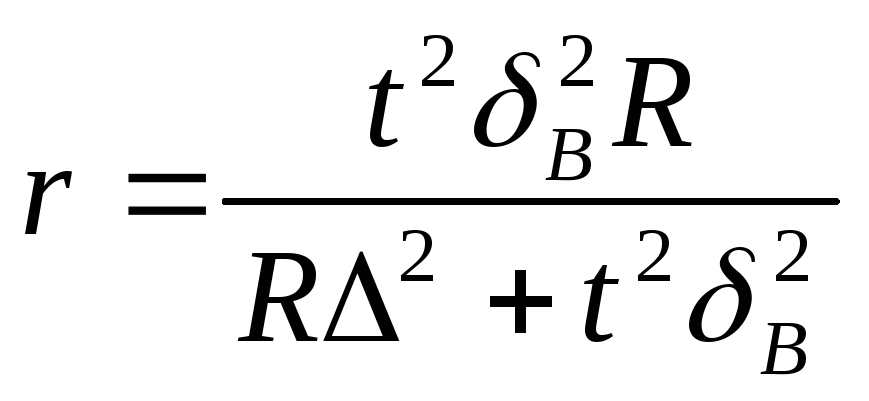