4.4. Розрахунок моди і медіани

Методичні вказівки

Узагальнюючими показниками варіаційних рядів разом з середніми є мода і медіана.

Мода - величина ознаки (варіанту), що найчастіше повторюється в сукупності, що вивчається.

Для дискретних рядів розподілу модою буде значення варіанти з найбільшою частотою.

Для інтервальних рядів розподілу з рівними інтервалами мода визначається по формулі:

,

(4.8)

- нижнє значення (межа) модального інтервалу (інтервалу, що містить моду);

- розмір (величина) модального інтервалу;

- частота модального інтервалу;

,- частота інтервалу, відповідно передуючого і наступного за модальним.

Медіаною в статистиці називається варіанту, розташована в середині варіаційного ряду.

Якщо ряд розподілу дискретний і має непарне число членів, то медіаною буде варіант, що знаходиться в середині впорядкованого ряду:

,

(4.9)

Якщо впорядкований ряд складається з парного числа членів, то медіаною буде середня арифметична з двох варіант, розташованих в середині ряду, тобто:

,

(4.10)

Для інтервальних рядів розподілу з рівними інтервалами медіана визначається по формулі:

,

(4.11)

де х^н_Ме - нижня межа (значення) медіанного інтервалу;

- величина (розмір) медіанного інтервалу;

- сума частот ряду розподілу;

- частота медіанного інтервалу;

- сума накопичених частот, передуючих медіанному інтервалу.

Задачі

4.16. За даними задачі 4.1 визначте моду і медіану виробітки робітника за годину.

4.17. За даними задачі 4.2 визначте моду і медіану видобутку вугілля за добу.

4.18. Визначите моду і медіану, використовуючи для цього дані: 1) задачі 4.3; 6) задачі 4.4.

4.19. Визначите моду і медіану вартості основних фондів підприємства, використовуючи для цього дані задачі 4.5.

4.20. За даними задачі 4.6 визначте моду і медіану міцності нитки.

Тема 5. Показники варіації і форми розподілу

Практичні заняття по темі передбачають вирішення наступних типів задач: 1) визначення розмаху варіації, середнього лінійного і квадратичного відхилень і коефіцієнтів варіації; 2) розрахунок дисперсії; 3) розрахунок групової, міжгрупової і загальної дисперсії; 4) визначення показників, що характеризують форму розподілу; 5) розрахунок критеріїв злагоди: Пірсона і Колмогорова.

5.1. Визначення розмаху варіації, середнього лінійного і квадратичного відхилення, коефіцієнтів варіації

Методичні вказівки

Розмах варіації визначається як різниця між найбільшим (x_max) і найменшим (x_min) значенням ознаки:

R = xmax – xmin .

(5.1)

Розрахунок середнього лінійного () ісереднього квадратичного () відхилень за індивідуальними даними виконується по формулах:

,	(5.2)
,	(5.3)

У дискретних рядах розподілу формули мають вигляд:

,	(5.4)
,	(5.5)

У інтервальних рядах розподілу ці показники визначаються по формулах:

,	(5.4)
,	(5.5)

де x^’_j - середнє значення (середина) інтервалу j-тої групи;

т – загальне число груп.

Середнє лінійне і середнє квадратичне відхилення - величини іменовані і виражаються в одиницях виміру ознаки.

При порівнянні варіація різних ознак використовують відносні характеристики – коефіцієнти варіації.

Коефіцієнти варіації розраховуються по формулах:

- лінійний:

% ;

(5.6)

- квадратичний:

% ;

(5.7)

• осциляції:

% .

(5.8)

Задачі

5.1. За даними задачі 4.1 визначте розмах варіації, середнє лінійне і квадратичне відхилення, коефіцієнти варіації.

5.2. За даними задачі 4.2 визначте розмах варіації, середнє лінійне і квадратичне відхилення, коефіцієнти варіації.

5.3. Визначте розмах варіації, середнє лінійне і квадратичне відхилення і коефіцієнти варіації, використовуючи для цього дані: 1) задачі 4.3; 2) задачі 4.4.

5.4. За даними задачі 4.5 визначте розмах варіації, середнє лінійне і квадратичне відхилення, коефіцієнти варіації.

5.5. Використовуючи дані задачі 4.6 визначте розмах варіації, середнє лінійне відхилення, середнє квадратичне відхилення, коефіцієнти варіації.
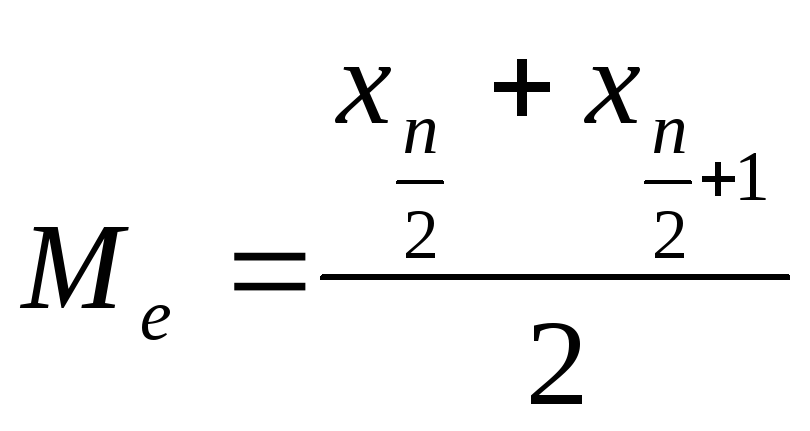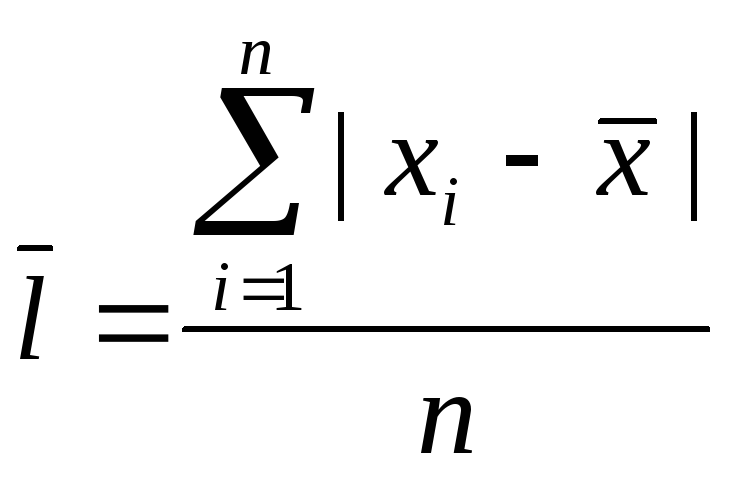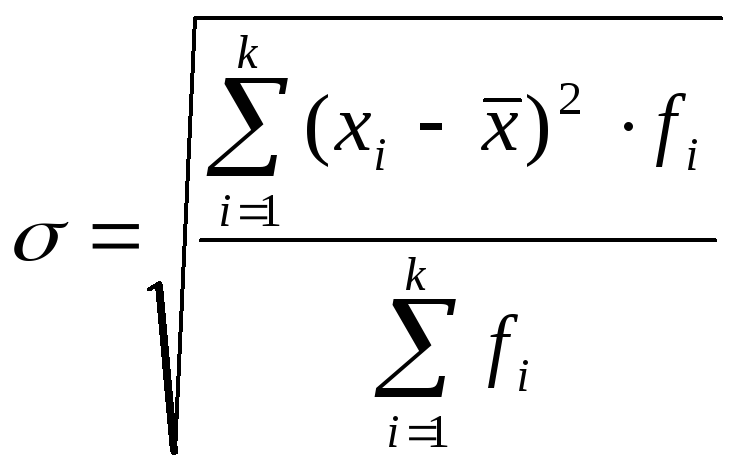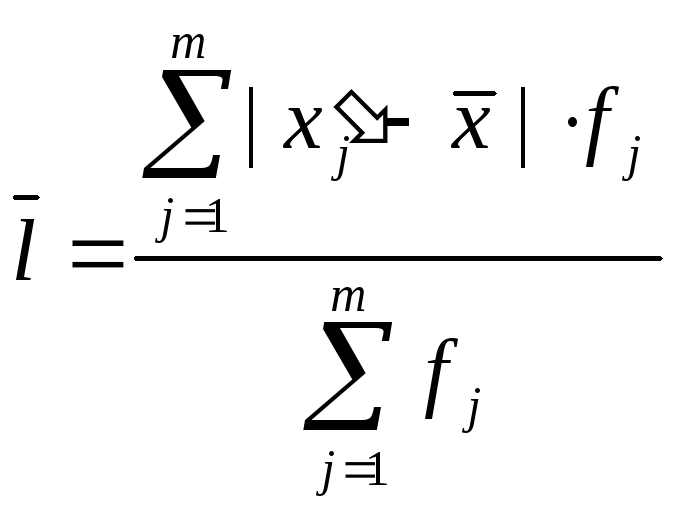