5.2. Розрахунок дисперсії

Методичні вказівки

Дисперсія - це середня арифметична квадратів відхилень кожного значення ознаки від загальної середньої.

В залежності від вихідних даних дисперсія може обчислюватися по різних формулах:

1. Якщо дисперсію потрібно обчислювати за індивідуальними даними кожної одиниці сукупності, то використовується формула дисперсії простої (не зваженої):

.

(5.9)

2. Якщо вихідні дані представлені у вигляді дискретного ряду розподілу, то використовується формула дисперсії зваженої:

.

(5.10)

3. Якщо вихідні дані представлені у вигляді інтервального ряду розподілу, то використовується наступна формула:

.

(5.11)

4. При великих значеннях варіантів і частот в інтервальних радах розподілу розрахунок дисперсії можна спростити, застосовуючи спосіб моментів:

.

(5.12)

де h - величина (розмір) інтервалу;

x^’_j - перетворені значення варіантів. Перетворення значень варіантів здійснюється по формулі:

,

(5.13)

А - постійна величина в якості якої зручно використовувати середину інтервалу, що має найбільшу частоту;

,	(5.14)
,	(5.15)

5. дисперсія альтернативної ознаки визначається по формулі:

,

(5.16)

де р - доля одиниць, що характеризуються досліджуваною ознакою.

Задачі

5.6. За даними задачі 4.2 визначте дисперсію добового видобутку вугілля на шахті.

5.7. Визначте дисперсію, використовуючи для цього дані: 1) задачі 4.4; 2) задачі 4.5.

5.8. Розрахуйте дисперсію за способом моментів за даними: 1) задачі 4.6; 2) задачі 4.9.

5.9. У пологовому будинку за добу народилося 30 дітей, з них 19 - дівчатка. Визначте дисперсію долі дівчаток, що народилися, в загальній чисельності новонароджених.

5.3. Розрахунок групової, міжгрупової і загальної дисперсії

Методичні вказівки

Загальна дисперсія дорівнює середньому квадрату відхилень окремих значень ознаки від загальної середньої. Вона відображає варіацію ознаки за рахунок всіх умов і причин, що діють в сукупності.

Загальна середня може бути обчислена по формулі:

.

(5.17)

Групова дисперсія ()дорівнює середньому квадрату відхилень значень ознаки усередині групи від середньої арифметичної цієї групи (групової середньої).

Вона може бути обчислена по формулі:

,

(5.18)

де x_ij – i-те значення ознаки, що входить до j-тої групи;

- середня арифметична ознаки j-тої групи (групова середня);

f_ij – частота і-того значення ознаки, що входить до j-тої групи;

l – загальна кількість значень ознаки, що входить до j-тої групи.

Ця дисперсія відображає варіацію ознаки лише за рахунок умов і причин, що діють усередині групи.

Середня з групових дисперсій () - це середня арифметична зважена з дисперсій групових:

,

(5.19)

де т – загальне число груп;

f_j – вага (частота) j-тої групи в загальній сукупності.

Міжгрупова дисперсія дорівнює середньому квадрату відхилень групових середніх від загальної середньої:

,

(5.20)

Міжгрупова дисперсія характеризує варіацію результативної ознаки за рахунок групувальної ознаки.

Між вказаними видами дисперсій існує певне співвідношення:

,

(5.21)

Це співвідношення називають правилом складання дисперсій.

Задачі

5.10. Є наступні дані про продуктивність праці робітників:

Табельний номер робітника	Обсяг випущеної продукції, шт
	у денну зміну	у нічну зміну
1	5	5
2	8	6
3	7	4
4	4	4
5	6	6

Обчисліть: 1) групові дисперсії; 2) середню з групових дисперсій; 3) міжгрупову дисперсію; 4) загальну дисперсію (за правилом складання дисперсій і звичайним способом).

5.11. Є показники розподілу основних фондів по заводах галузі:

Групи заводів по вартості основних фондів, млн. грн.	Число заводів	Середня вартість основних фондів, млн. грн.	Групові дисперсії
1.2-2.7	9	1.8	0.17
2.7-4.2	11	3.2	0.09
4.2-5.7	7	4.8	0.25

Визначите загальну дисперсію основних фондів по сукупності заводів, застосовуючи правило складання дисперсій.

5.12. Є наступні дані про розподіл робітників цеху по відсотку браку, що допускається в процесі виробництва:

Відсоток браку	Число робітників	Середній відсоток браку продукції на одного робітника	Середнє квадратичне відхилення
до 1	7	0.8	0.67
1-3	20	2.3	0.65
3-5	15	3.7	0.51
5-7	5	5.9	0.48

Обчисліть загальну дисперсію браку продукції, що допускається робітниками, застосовуючи правило складання дисперсій.
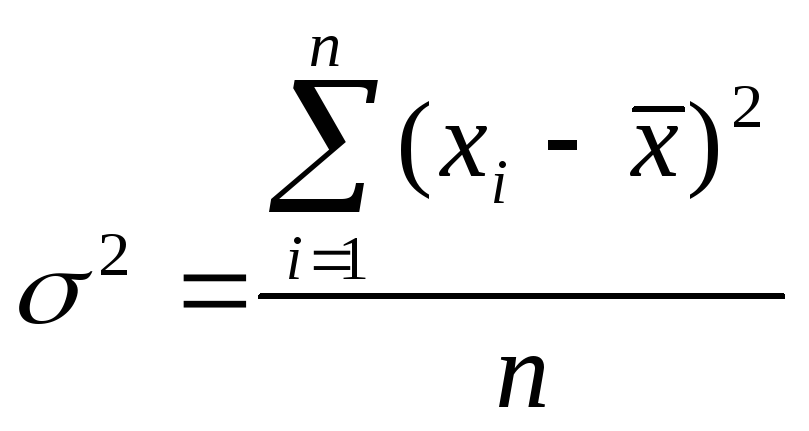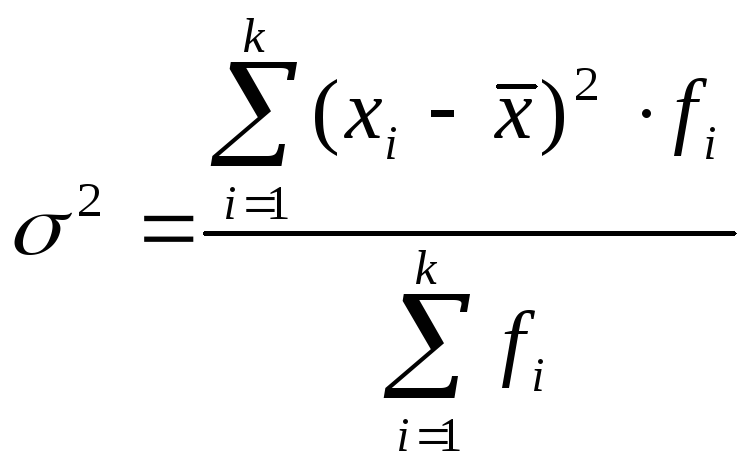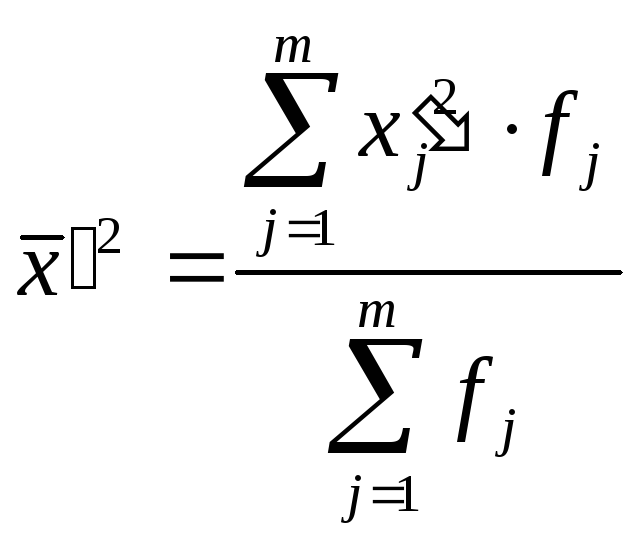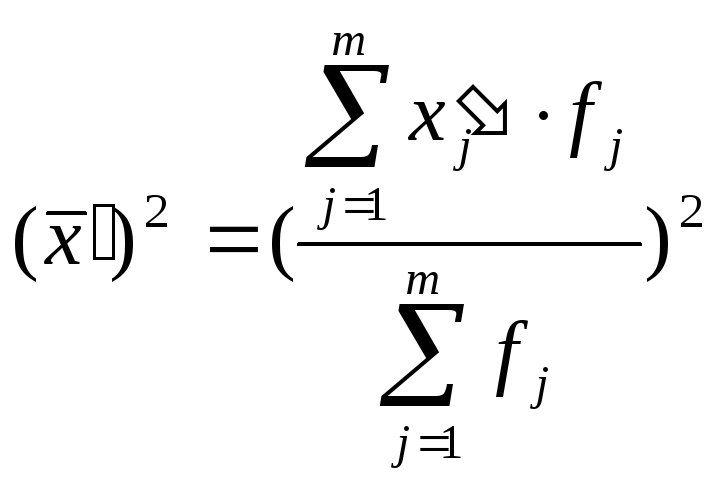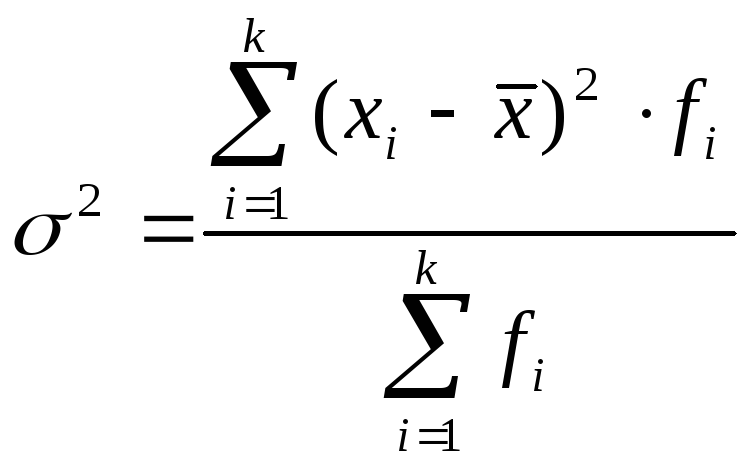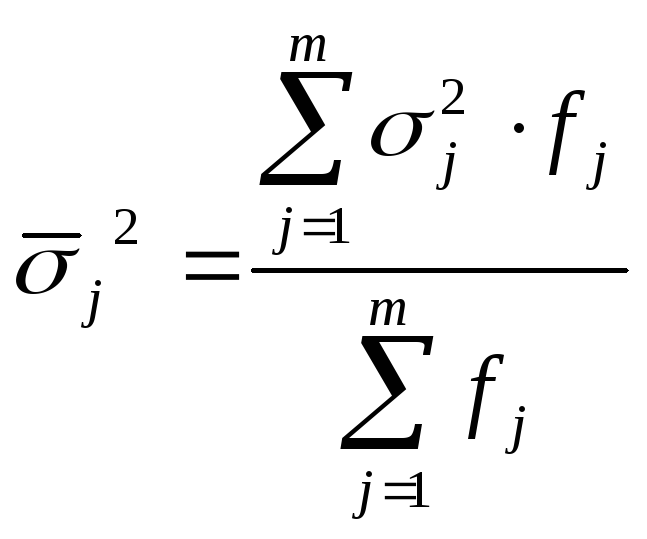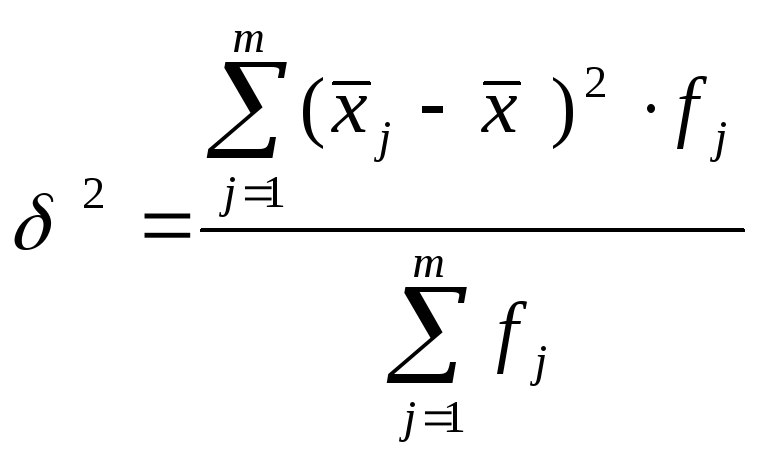