Контрольні запитання

1. У чому суть методу найменших квадратів?

2. Які основні причини наявності в регресійній моделі випадкового відхилення?

3. Як розрахувати невідомі параметри лінійної моделі?

4. Пояснити сутність поняття "тіснота зв'язку".

5. Пояснити сутність поняття "значимість зв'язку".

6. За допомогою яких характеристик перевіряються тіснота зв'язку між змінними моделі?

7. За допомогою якої характеристики перевіряються значимість зв'язку між змінними моделі?

8. Що показує коефіцієнт детермінації і в яких межах він приймає значення?

9. Що показує коефіцієнт кореляції?

10. Запишіть формулу дисперсії залишків.

11. З якою ціллю розраховуються стандартні похибки оцінок параметрів?

12. За якими характеристиками вибирається табличне значення критерію Фішера?

13. Як визначити коефіцієнт детермінації у парній регресійній моделі?

14. Як визначити коефіцієнт кореляції у парній регресійній моделі?

15. У чому відмінність між точковим і інтервальним прогнозом?

Література: [3, с. 233-263; 5, с. 415-463; 8, с. 25-38; 9, с. 43-46,96-106, 111-130; 10, с. 44-60,63-65,102; 11, с. 23-29, 113-120, 127-140; 12, с. 41-58].

Тема № 8. Функції і графіки в економетричному моделюванні Лабораторна робота № 7 «Пошук взаємозалежності між економічними процесами»

Постановка задачі.

Результатом спостережень, або вимірювань показників є таблиця значень цих показників. Розробити емпіричну (дослідну) модель залежності Y від Х, яка мінімально відрізняється від дослідних даних.

Згідно варіанту (додаток 16) дослідити залежність одного економічного показника (Y) від іншого (X). Передбачається, що залежність між Y та Х може бути:

Лінійна
Гіперболічна
Параболічна
Ступінна
Експоненціальна
Проста модифікована експоненціальна

Мета роботи:

1. Визначити аналітичну залежність між дослідними даними.

2. Знайти параметри моделі.

3. Провести оцінку тісноти на значимості зв’язку між показниками моделі (Y, X).

4. Провести оцінку точності отриманої моделі.

5. Обчислити прогнозні значення Y_пр (точковий прогноз).

6. Представити модель на графіку.

Алгоритми побудови моделей

Модель лінійної регресії (лінійне рівняння) є найпоширенішим видом залежності між економічними змінними. Скористаймося методом найменших квадратів, суть якого полягає у наступному: сума квадратів відхилень ординат точки, що спостерігається (X_i, Y_i) від відповідної ординати точки, що лежить на регресійній прямій, повинна бути найменшою

Використання 1МНК для оцінки теоретичних параметрів моделі парної регресії приводить до таких систем нормальних рівнянь:

1. лінійна залежність Y = a₀ + a₁X.

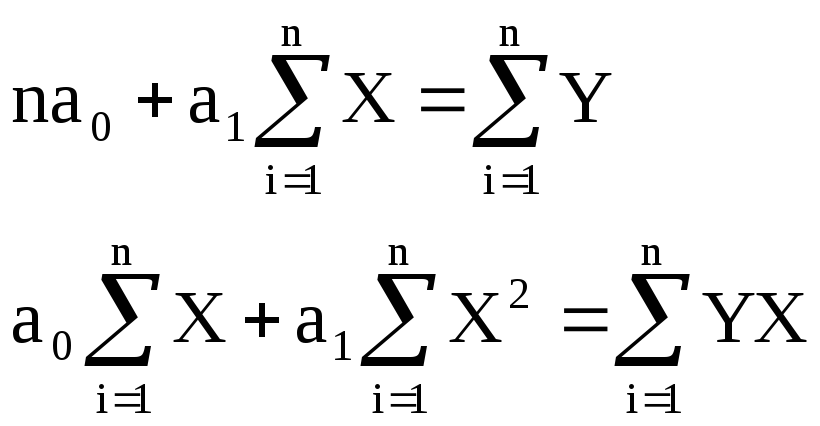
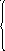
Побудоване лінійне рівняння може слугувати початковою точкою в разі складних (суттєво нелінійних) залежностей.

Нелінійні зв'язки, як правило, певними перетвореннями (заміною змінних чи логарифмуванням) зводять до лінійного вигляду або апроксимують (наближують) лінійними функціями.

2) гіперболічна залежність .Замінюємо і отримаємо лінійну модель Y = a₀ + a₁х′.

Для оцінки теоретичних параметрів моделі складаємо систему нормальних рівнянь:

3) параболічна залежність Y = a₀ + a₁х² . Замінюємо х² = х′ і отримаємо лінійну модель Y = a₀ + a₁х′.

Для оцінки теоретичних параметрів моделі складаємо систему нормальних рівнянь:

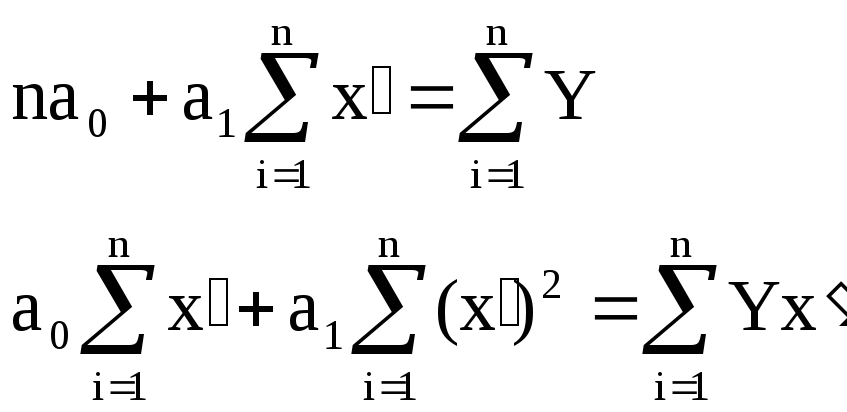
4) степенева залежність .

Логарифмуємо функцію lnY = ln a₀ + a₁ · ln Х.

Замінюємо логарифми lnY = Y′, ln Х = Х′ , ln a₀ = a′.

Одержуємо лінійну модель Y′ = a′+ a₁ · Х′.

Складаємо систему нормальних рівнянь:

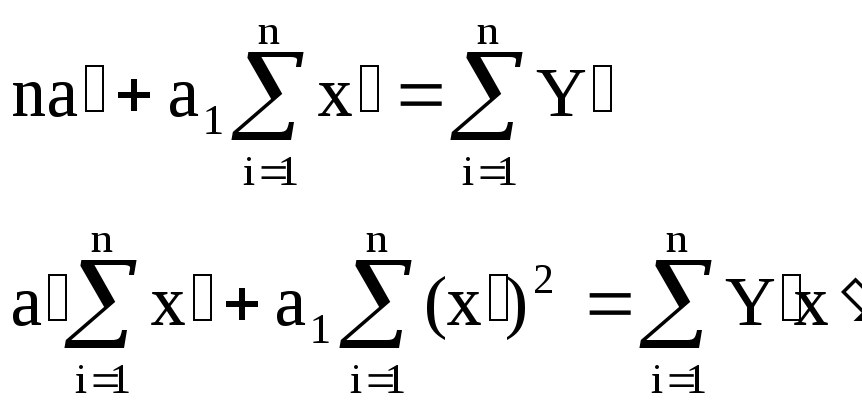
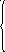
5) експоненціальна .

Для оцінки теоретичних параметрів зводимо модель до лінійного вигляду.

Логарифмуємо функцію

Замінюємо логарифми

Одержуємо лінійну модель

6) проста модифікована експоненціальна

Методом заміни зводимо модель до лінійного вигляду:

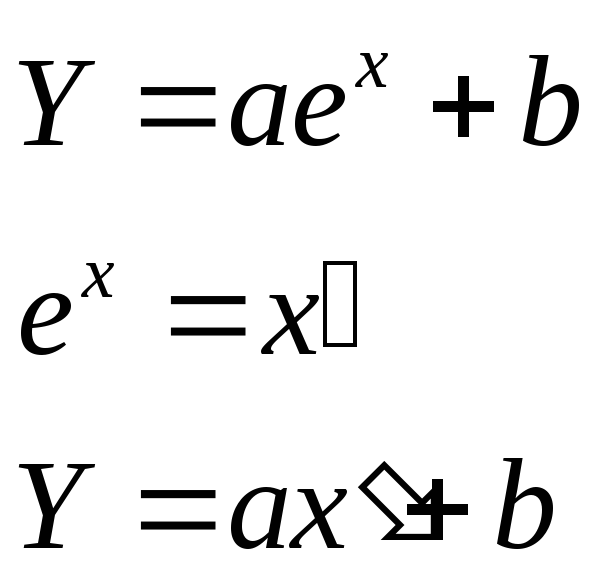
Результати розрахунків зводимо до таблиці 7.1.

Таблиця 7.1

	a	b	с	R2	F	R
Модель 1
Модель 2
Модель 3
Модель 4
Модель 5
Модель 6
				max

В економічних розрахунках вважається прийнятним такий зв’язок між факторами, при якому R² > 0,7. Всі інші фактори можуть не включатися в подальші розрахунки рівнянь регресії.

Припустимо, що для опису одного економічного процесу придатні дві моделі. Обидві адекватні за F-критерієм Фішера. Перевагу надають моделі з більшим коефіцієнтом детермінації.