
- •Preface
- •Acknowledgements
- •Contents
- •1.1 Introduction
- •1.2 Classical Physics Between the End of the XIX and the Dawn of the XX Century
- •1.2.1 Maxwell Equations
- •1.2.2 Luminiferous Aether and the Michelson Morley Experiment
- •1.2.3 Maxwell Equations and Lorentz Transformations
- •1.3 The Principle of Special Relativity
- •1.3.1 Minkowski Space
- •1.4 Mathematical Definition of the Lorentz Group
- •1.4.1 The Lorentz Lie Algebra and Its Generators
- •1.4.2 Retrieving Special Lorentz Transformations
- •1.5 Representations of the Lorentz Group
- •1.5.1 The Fundamental Spinor Representation
- •1.6 Lorentz Covariant Field Theories and the Little Group
- •1.8 Criticism of Special Relativity: Opening the Road to General Relativity
- •References
- •2.1 Introduction
- •2.2 Differentiable Manifolds
- •2.2.1 Homeomorphisms and the Definition of Manifolds
- •2.2.2 Functions on Manifolds
- •2.2.3 Germs of Smooth Functions
- •2.3 Tangent and Cotangent Spaces
- •2.4 Fibre Bundles
- •2.5 Tangent and Cotangent Bundles
- •2.5.1 Sections of a Bundle
- •2.5.2 The Lie Algebra of Vector Fields
- •2.5.3 The Cotangent Bundle and Differential Forms
- •2.5.4 Differential k-Forms
- •2.5.4.1 Exterior Forms
- •2.5.4.2 Exterior Differential Forms
- •2.6 Homotopy, Homology and Cohomology
- •2.6.1 Homotopy
- •2.6.2 Homology
- •2.6.3 Homology and Cohomology Groups: General Construction
- •2.6.4 Relation Between Homotopy and Homology
- •References
- •3.1 Introduction
- •3.2 A Historical Outline
- •3.2.1 Gauss Introduces Intrinsic Geometry and Curvilinear Coordinates
- •3.2.3 Parallel Transport and Connections
- •3.2.4 The Metric Connection and Tensor Calculus from Christoffel to Einstein, via Ricci and Levi Civita
- •3.2.5 Mobiles Frames from Frenet and Serret to Cartan
- •3.3 Connections on Principal Bundles: The Mathematical Definition
- •3.3.1 Mathematical Preliminaries on Lie Groups
- •3.3.1.1 Left-/Right-Invariant Vector Fields
- •3.3.1.2 Maurer-Cartan Forms on Lie Group Manifolds
- •3.3.1.3 Maurer Cartan Equations
- •3.3.2 Ehresmann Connections on a Principle Fibre Bundle
- •3.3.2.1 The Connection One-Form
- •Gauge Transformations
- •Horizontal Vector Fields and Covariant Derivatives
- •3.4 Connections on a Vector Bundle
- •3.5 An Illustrative Example of Fibre-Bundle and Connection
- •3.5.1 The Magnetic Monopole and the Hopf Fibration of S3
- •The U(1)-Connection of the Dirac Magnetic Monopole
- •3.6.1 Signatures
- •3.7 The Levi Civita Connection
- •3.7.1 Affine Connections
- •3.7.2 Curvature and Torsion of an Affine Connection
- •Torsion and Torsionless Connections
- •The Levi Civita Metric Connection
- •3.8 Geodesics
- •3.9 Geodesics in Lorentzian and Riemannian Manifolds: Two Simple Examples
- •3.9.1 The Lorentzian Example of dS2
- •3.9.1.1 Null Geodesics
- •3.9.1.2 Time-Like Geodesics
- •3.9.1.3 Space-Like Geodesics
- •References
- •4.1 Introduction
- •4.2 Keplerian Motions in Newtonian Mechanics
- •4.3 The Orbit Equations of a Massive Particle in Schwarzschild Geometry
- •4.3.1 Extrema of the Effective Potential and Circular Orbits
- •Minimum and Maximum
- •Energy of a Particle in a Circular Orbit
- •4.4 The Periastron Advance of Planets or Stars
- •4.4.1 Perturbative Treatment of the Periastron Advance
- •References
- •5.1 Introduction
- •5.2 Locally Inertial Frames and the Vielbein Formalism
- •5.2.1 The Vielbein
- •5.2.2 The Spin-Connection
- •5.2.3 The Poincaré Bundle
- •5.3 The Structure of Classical Electrodynamics and Yang-Mills Theories
- •5.3.1 Hodge Duality
- •5.3.2 Geometrical Rewriting of the Gauge Action
- •5.3.3 Yang-Mills Theory in Vielbein Formalism
- •5.4 Soldering of the Lorentz Bundle to the Tangent Bundle
- •5.4.1 Gravitational Coupling of Spinorial Fields
- •5.5 Einstein Field Equations
- •5.6 The Action of Gravity
- •5.6.1 Torsion Equation
- •5.6.1.1 Torsionful Connections
- •The Torsion of Dirac Fields
- •Dilaton Torsion
- •5.6.2 The Einstein Equation
- •5.6.4 Examples of Stress-Energy-Tensors
- •The Stress-Energy Tensor of the Yang-Mills Field
- •The Stress-Energy Tensor of a Scalar Field
- •5.7 Weak Field Limit of Einstein Equations
- •5.7.1 Gauge Fixing
- •5.7.2 The Spin of the Graviton
- •5.8 The Bottom-Up Approach, or Gravity à la Feynmann
- •5.9 Retrieving the Schwarzschild Metric from Einstein Equations
- •References
- •6.1 Introduction and Historical Outline
- •6.2 The Stress Energy Tensor of a Perfect Fluid
- •6.3 Interior Solutions and the Stellar Equilibrium Equation
- •6.3.1 Integration of the Pressure Equation in the Case of Uniform Density
- •6.3.1.1 Solution in the Newtonian Case
- •6.3.1.2 Integration of the Relativistic Pressure Equation
- •6.3.2 The Central Pressure of a Relativistic Star
- •6.4 The Chandrasekhar Mass-Limit
- •6.4.1.1 Idealized Models of White Dwarfs and Neutron Stars
- •White Dwarfs
- •Neutron Stars
- •6.4.2 The Equilibrium Equation
- •6.4.3 Polytropes and the Chandrasekhar Mass
- •6.5 Conclusive Remarks on Stellar Equilibrium
- •References
- •7.1 Introduction
- •7.1.1 The Idea of GW Detectors
- •7.1.2 The Arecibo Radio Telescope
- •7.1.2.1 Discovery of the Crab Pulsar
- •7.1.2.2 The 1974 Discovery of the Binary System PSR1913+16
- •7.1.3 The Coalescence of Binaries and the Interferometer Detectors
- •7.2 Green Functions
- •7.2.1 The Laplace Operator and Potential Theory
- •7.2.2 The Relativistic Propagators
- •7.2.2.1 The Retarded Potential
- •7.3 Emission of Gravitational Waves
- •7.3.1 The Stress Energy 3-Form of the Gravitational Field
- •7.3.2 Energy and Momentum of a Plane Gravitational Wave
- •7.3.2.1 Calculation of the Spin Connection
- •7.3.3 Multipolar Expansion of the Perturbation
- •7.3.3.1 Multipolar Expansion
- •7.3.4 Energy Loss by Quadrupole Radiation
- •7.3.4.1 Integration on Solid Angles
- •7.4 Quadruple Radiation from the Binary Pulsar System
- •7.4.1 Keplerian Parameters of a Binary Star System
- •7.4.2 Shrinking of the Orbit and Gravitational Waves
- •7.4.2.1 Calculation of the Moment of Inertia Tensor
- •7.4.3 The Fate of the Binary System
- •7.4.4 The Double Pulsar
- •7.5 Conclusive Remarks on Gravitational Waves
- •References
- •Appendix A: Spinors and Gamma Matrix Algebra
- •A.2 The Clifford Algebra
- •A.2.1 Even Dimensions
- •A.2.2 Odd Dimensions
- •A.3 The Charge Conjugation Matrix
- •A.4 Majorana, Weyl and Majorana-Weyl Spinors
- •Appendix B: Mathematica Packages
- •B.1 Periastropack
- •Programme
- •Main Programme Periastro
- •Subroutine Perihelkep
- •Subroutine Perihelgr
- •Examples
- •B.2 Metrigravpack
- •Metric Gravity
- •Routines: Metrigrav
- •Mainmetric
- •Metricresume
- •Routine Metrigrav
- •Calculation of the Ricci Tensor of the Reissner Nordstrom Metric Using Metrigrav
- •Index
204 |
5 Einstein Versus Yang-Mills Field Equations |
is the gauge covariant differential of the 0-form field F I |ab . As stated above, this object is both a section of the adjoint vector bundle associated with the principle bundle P (M , G) and an antisymmetric section of the Lorentz bundle. For this reason its covariant differential involves both the gauge connection A J and the spin connection ωac .
Let us analyze (5.3.44). What is the condition under which it reproduces the standard Yang-Mills equation that we obtain by varying the second order action (5.3.30)? The answer is encoded in the concept of soldering.
5.4 Soldering of the Lorentz Bundle to the Tangent Bundle
Suppose that we enforce the following equation:
Ta = 0 |
(5.4.1) |
what are its consequences?
First of all, with reference to (5.3.44) we note that it reduces to just the first addend. Secondly we note that F I |ab as defined in (5.3.45) is a one-form on the base manifold M . As such it can be expanded along a basis of sections of the cotangent bundle, in particular along the basis provided by the vielbein Ea . Hence we can write:
F I |ab = cF I |abEc |
(5.4.2) |
The tensor cF I |ab is defined by the position (5.4.2) and it is named the intrinsic covariant derivative of the Yang-Mills field strength. Comparison with the definition (5.3.45) implies that:
cF I |ab = Eaμ ∂μF I |ab + f IJ K AμJ F K|ab |
|
+ ωμacF I |cd ηcd + ωμbcF I |acηcd |
(5.4.3) |
which justifies its name. Indeed it is the covariant derivative of the tensor F where the Greek holonomic index μ has been anholonomized and converted into a Latin one through multiplication with the inverse vielbein. The meaning of this operation is that cF I |ab is now a section of the adjoint-bundle with respect to the internal gauge group G and a section of the triple power of the Lorentz bundle, while it behaves as a bona-fide scalar function with respect to the tangent bundle T M of the base-manifold.
Inserting (5.4.2) into (5.3.44) we obtain:
0 |
= d F I |ab Ed Ec1 · · · Ecm−2 εc1...cm−2ab |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dc |
...cm |
p |
m 1 |
||
|
|
|
ε |
Φp[ − ] |
|||||
|
|
|
1 |
−2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.4.4) |
|
0 |
= a F I |ab |
|
|
|
|
|
|
|
|
5.4 Soldering of the Lorentz Bundle to the Tangent Bundle |
205 |
In the above calculations which constitutes a prototype for all the following calculations of the present chapter and also for many of the calculations in later chapters, we have denoted by Φp[m−1] a basis of sections for the +[m−1][E] exterior product of the 1-form valued Lorentz bundle in the vector representation. In other words each element of +[m−1][E] is an exterior product of (m − 1) vielbein and there are exactly m independent such monomials. By means of the Levi Civita symbol they can be enumerated as follows:
Φ[m−1] = εc ...c − p Ec1 · · · Ecm−1 p 1 m 1
Equation (5.4.4) implies that the coefficients of the independent should separately vanish and using the straightforward identity:
εdc1...cm−2p × εc1...cm−2ab = (−)(m−2)(m − 2)!m!δabdp
(5.4.5)
(m − 1)-forms
(5.4.6)
this implies the last of (5.4.4). In it we recognize the standard dynamical field equation of a Yang-Mills field. Indeed reverting to Greek indices the last of (5.4.4) becomes:
μFμνI = 0 |
(5.4.7) |
where: |
|
ρ FμνI = ∂ρ FμνI − Γρμσ FσIν − Γρνσ FμσI + f IJ K AρJ FμνK |
(5.4.8) |
The symbol Γρμσ denotes the coefficient of the Levi Civita connection as defined in (3.7.14)–(3.7.16) and coincides with the Christoffel symbols (3.2.7).
The natural question that we expect from the attentive reader is the following: “What happened of the spin-connection coefficients ωμab which seem to have completely disappeared from the above rewriting of the dynamical equations?” The answer to this quite legitimate question encodes the whole fascination of the soldering mechanism defined by imposing (5.4.1).
Consider the vielbein Eμa and define its complete covariant derivative which is given below:
ρ Eμa ≡ ∂ρ Eμa − ωρabEμc ηbc − Γρμσ Eσa |
(5.4.9) |
In writing (5.4.9) we have carefully taken into account that Eμa is both a section of the tangent bundle T M and a section of the associated vector bundle to the principal Lorentz bundle. In its first quality the vielbein feels the Levi Civita connection Γρμσ , in its second quality it feels the Lorentz connection ωρab . We assume two equations:
1.The vanishing of the torsion (5.4.1), which can be rephrased as D[μEνa] = 0
where DμEνa ≡ ∂μEνa − ωμabEνcηbc .
2.The covariant constancy of the metric ρ gμν = 0 which, together with the symmetricity of Γρμσ in its lower indices, defines the Levi Civita connection.
206 |
5 Einstein Versus Yang-Mills Field Equations |
Equation D[μEνa] = 0 suffices to completely and uniquely determine the coefficients of the spin connection ωρab in terms of the vielbein derivatives and of its inverse. A simple counting explains why. The total number of unknowns in an m-dimensional manifold is 12 m2(m − 1). The same is the number of linear equations provided by the condition of vanishing torsion. Explicitly the solution can be obtained by means of a trick completely analogous to that used to determine the Levi Civita connection. Introduce the contorsion, defined below:
Kpqa ≡ EpμEqν ∂[μEνa] |
(5.4.10) |
and the latinized components of the spin connection: |
|
ωrab = Erμωμab |
(5.4.11) |
In terms of these objects the vanishing torsion equation becomes: |
|
2Kpqa = ωpabηqb − ωqabηpb |
(5.4.12) |
By summing three copies of the above equations with cyclically permuted indices, using the antisymmetry of the contorsion in its lower indices and that of the spin connection in its upper ones, the solution for ωpab in terms of Kpqa is explicitly obtained. This conclusion is quite momentous. It implies that the Lorentz gauge connection is not an independent dynamical object, rather it is completely determined by the vielbein, just as the Levi Civita connection is completely determined by the metric. The equivalency of the metric and vielbein formalism arises from the already proposed identification of the metric with the quadratic form in the vielbein which was spelled out in (5.2.9). Combining the latter with the covariant constancy of the metric with respect to the Levi Civita connection we obtain:
ρ Eμa Eνb + Eμa ρ Eνb ηab = 0 |
(5.4.13) |
Implementing once again the standard trick of rewriting three copies of the above equation with permuted indices
0 = ρ Eμa Eνb + Eμa ρ Eνb ηab |
|
0 = − μEνbEρa + Eνb μEρa ηba |
(5.4.14) |
0 = − ν Eρb Eρa + Eρb ν Eμa ηba |
|
and summing them together, upon use of the vanishing torsion equation [ρ Eμa ] = 0 we obtain that also the symmetric combination of derivatives vanishes.
μEνa + ν Eμa = 0 |
(5.4.15) |
Hence we conclude that: |
|
μEνa = 0 |
(5.4.16) |
5.4 Soldering of the Lorentz Bundle to the Tangent Bundle |
207 |
Equation (5.4.16) is of the utmost relevance. It implies that, provided the torsion two-forms Ta vanishes, the tangent bundle and the Lorentz bundle are completely soldered to each other and we can trade the Levi Civita connection for the spinconnection and vice-versa.
In practice this means the following. Given any world tensor:
ν1 |
...νs |
(5.4.17) |
Tμ1...μr |
|
with r controvariant and s covariant indices, which is therefore a section of the rth power of the cotangent bundle T M and a section of the sth power of the tangent bundle T M , through multiplication with an appropriate number of direct and inverse vielbein we can convert it into a corresponding section of the (r, s)th power of the associated Lorentz vector bundle:
Ta1...ar b1...bs = Eaμ11 . . . Eaμrr Eνb11 . . . Eνbrr Tμ1...μr ν1...νs |
(5.4.18) |
Soldering means that the parallel transport by means of the spin connection in the Lorentz bundle is completely equivalent to the parallel transport on the tangent/cotangent bundle by means of the Levi Civita connection. Introducing the curly capital D as a notation for the Lorentz-covariant differential of any Lorentz-tensor valued p-form, namely:
D T a1...ar ≡ dT a1...ar − ωa1b1 T c1a2...ar ηb1c1 · · · − ωar br T a1a2...cr ηbr cr
(5.4.19)
and reserving the symbol for the Levi Civita covariant differential of any worldtensor valued p-form:
T |
μ1...μr |
≡ dT |
μ1...μr |
− Γ |
μ1 |
T |
ν1μ2...μr |
· · · − Γ |
μr |
T |
μ1μ2... |
νr |
(5.4.20) |
|
|
ν1 |
|
νr |
|
|
the soldering (5.4.16) guarantees that we can write:
D T a1...ar = Eμa11 . . . Eμarr T μ1...μr
(5.4.21)
T μ1...μr = Eaμ11 . . . Eaμrr D T a1...ar
5.4.1Gravitational Coupling of Spinorial Fields
The results of the previous section show that as far as tensor fields are concerned the use of the Levi Civita connection or of the spin-connection in the vielbein formalism are completely equivalent. This equivalence does not extend to the case of spinorial fields. As we emphasized more than once, spinorial representations are a specific feature of the orthogonal or pseudo-orthogonal algebras, so that spinorial sections of the tangent or cotangent bundle do not exists. On the other hand given the principal Lorentz bundle, we can construct all of its associated spinorial bundles. This
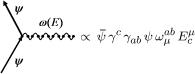
208 |
5 Einstein Versus Yang-Mills Field Equations |
Fig. 5.3 The gravitational interaction vertex of spin 1/2 particles
amounts to saying that via the spin connection ωab we can easily define the covariant derivative of any spinor field and this, thanks to the soldering condition, which expresses ωab in terms of the vielbein, introduces the gravitational coupling of the spinor particles.
We already shew how to rewrite the Yang-Mills Lagrangian in vielbein formalism. Let us now consider the case of the Dirac Lagrangian for a spin one half field. As usual, in preparation for those multi-dimensional theories that constitute the focus of attention in contemporary Theoretical Physics, we deal with the case of spinor fields in m-dimensions. For conventions and properties of spinor fields in diverse dimensions we refer the reader to Appendix A. Here for simplicity we focus on the case of a Dirac spinor which always exists in every dimension. In Minkowski space the free Dirac action is the following one which is the direct generalization to dimension m of the action considered in (5.3.7):
ADirac |
|
iψγ μ∂μψ dmx |
(5.4.22) |
||
|
= |
|
|
|
|
It can be easily recast in a general covariant form and adapted to a curved space-time manifold through the following rewriting:
A |
(cov) |
= |
|
1 |
|
|
|
|
i |
|
γ a1 D ψ |
|
Ea2 |
|
Ea3 |
· · · |
Eam εa |
|
|
|
|
|
ψ |
...am |
|||||||||||||
Dirac |
(m |
|
1) |
|||||||||||||||
|
− |
|
|
|
|
|
|
1 |
(5.4.23) |
|||||||||
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
||||
|
D ψ ≡ dψ − |
1 |
ωabγabψ |
|
|
|
|
|
|
|
||||||||
|
|
4 |
|
|
|
|
|
|
|
|||||||||
The reader will notice that the ingredients entering (5.4.23) are just the vielbein Ea and the spin connection ωab , namely the components of the principal connection on the Poincaré bundle. The above action is manifestly invariant against local Lorentz transformations and it is invariant against general diffeomorphisms on the base manifold M , since it is written in terms of differential forms and their exterior products. When the spin connection ωab vanishes and the vielbein reduces to a Krönecker delta function, which is the case of flat Minkowski space, the reader can easily verify that the actions (5.4.23) and (5.4.22) coincide. However, just as the U(1) covariant derivative in the case of electrodynamics produced an interaction vertex of the fermion field with the photon field, in the same way, the Lorentz-covariant derivative used in the action (5.4.23) generates a non-trivial interaction vertex of the same fermionic field with the graviton, which has a universal structure and it is illustrated in Fig. 5.3. Having clarified the advantages and power of the vielbein formalism we just adopt it throughout most of the following exposition, turning to the fundamental question of Einstein equations, namely to the dynamics of the gravitational field.
