3.2.3 Parallel Transport and Connections

Fig. 3.5 The parallel transport of a vector along a curve is defined through the preservation of its angle with the tangent vector. This definition is possible if we have a metric and hence the notion of scalar product of local vectors

notion of the metric gik (x), introduced in (3.2.3). Once the metric is established, a natural way arises of transporting vectors along any given curve xμ(λ). We can say that a vector is parallel-transported along an arc of curve if the angle between the transported vector and the tangent vector to the curve remains constant throughout the entire transport (see Fig. 3.5).

This notion is meaningful if we can define and measure angles. This is precisely what the existence of a metric allows. Indeed, in presence of gμν (x), we can generalize the relations of Euclidian geometry by defining the norm of any vector as:

The metric connection is that infinitesimal displacement of a vector X along the direction singled out by another one Y which is so defined as to fulfill the property of preserving angles. It was first conceived by Christoffel.

Elwin Bruno Christoffel was born in 1829 in Montjoie, near Aachen, that was renamed Monschau in 1918 (Fig. 3.6). After attending secondary schools in Cologne, he enrolled at the University of Berlin, where he had such teachers as Eisenstein and Dirichlet. Particularly the latter is duely considered his master. Christoffel’s doctor dissertation, dealing with the motion of electricity in homogeneous media was defended in 1856, just two years after Riemann’s presentation of the Ueber die Hypothesen. Having spent a few years out of the academic world, Christoffel returned to Mathematics in 1859, obtaining his habilitation from Berlin University. In the following years he was professor at the Polytechnic of Zürich, at the newly

Fig. 3.6 Elwin Bruno (Montjoie 1829, Strasbourg 1918)

founded Technical University of Berlin and finally at the University of Strasbourg which had become German after the defeat of Napoleon III in the 1870 war. According to opinions reported by contemporaries, Elwin Bruno Christoffel was one of the most polished teachers ever to occupy a chair. His lectures were meticulously prepared and his delivery was lucid and of the greatest aesthetic perfection. . . The core of his course was the theory of complex functions that he developed and presented according to Riemann’s approach.

Although he wrote papers on several different topics like potential theory, differential equations, conformal mappings, orthogonal polynomials and still more, the most relevant and influential of Christoffel’s contributions with the furthest reaching consequences was his invention of the three-index symbols that bear his name. Defined in terms of a metric gμν (x) and of its inverse gρσ (x), the symbols:

are the first example of connection coefficients, actually those of the Levi Civita connection, that preserves angles along the parallel transport it defines [3].

Christoffel symbols are the key ingredients in the definition of the covariant derivative of a tensor (in particular of a vector):

The word tensor was introduced for the first time by Hamilton in 1846, but tensor calculus was developed around 1890 by Gregorio Ricci Curbastro under the title of absolute differential calculus and was made accessible to mathematicians by the

Fig. 3.7 The three Italian fathers of tensor calculus also named, at the time, Absolute Differential Calculus

publication of Tullio Levi Civita’s 1900 classic text of the same name, originally written in Italian, later republished in French with Ricci [4].

Gregorio Ricci Curbastro (see Fig. 3.7) was son in an aristocratic family of Lugo di Romagna. On the house where he was born in 1853 there stands a plate with the following words Diede alla scienza il calcolo differenziale assoluto, strumento

Fig. 3.8 The images of the same vector parallel transported along two different paths that converge at the same point of a manifold, generically differ by a rotation angle. That angle is a measure of the intrinsic curvature of the manifold and it is the information codified in the Riemann-Christoffel tensor

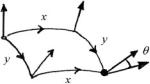
The geometrical meaning of this relation is exemplified in Fig. 3.8. Consider an infinitesimally small rectangle whose two sides are given by the two vectors Xμ and Y μ (also of infinitesimally short length), departing from a given point p. Consider next the parallel transport of a third vector V ρ to the opposite site of the rectangle. This parallel transport can be performed along two routes, both arriving at the same destination. The first route follows first X and then Y . The second route does the opposite. The image vectors of these two transports are based at the same point, so they can be compared, in particular they can be subtracted. So doing we find:

X Y V ρ − Y X V ρ = XμY ν [ μ ν ]V ρ + X Y σ − Y Xσ σ V ρ

= XμY ν V σ Rμνσ ρ + T σμν σ V ρ + [X, Y ]σ σ V ρ

(3.2.12)

where the Riemann-Christoffel tensor was defined above and where:

is another tensor named the torsion. In the case of the Christoffel symbols the torsion is identically zero, yet for more general connections it can be different from zero and Levi Civita correctly singled out the vanishing of the torsion as one of the two axioms from which the metric connection can be derived. In any case comparison of (3.2.12) with Fig. 3.8 enlightens the geometrical meaning of both torsion and curvature. If torsion is zero the parallel transport along the two different paths produces two vectors that differ from one another by a rotation angle and the Riemann tensor Rμνσ ρ encodes all these possible angles. If torsion is not zero the two images of parallel transport differ also by a displacement and the torsion tensor Tμλρ encodes all such possible displacements. In a flat space, just as a plane, parallel transport produces no rotation angle and no displacement. Hence the Riemann-Christoffel tensor

ρ measures the intrinsic curvature of a metric manifold.

In a paper of 1903 [6], Gregorio Ricci introduced a new tensor, later named after him, which is obtained from the Riemann-Christoffel tensor through a contraction of indices. The Ricci tensor is defined as follows:

group-theoretical view of geometry and one of his major achievements is precisely along that line. In a paper of 1898 [8], Bianchi classified all tridimensional spaces that admit a continuous group of motions. Actually, so doing, he classified all Lie algebras of dimension three. This classification, which is organized into nine types, turned out to be quite relevant for Cosmology in the framework of General Relativity, since it amounts to a classification of all possible space-times that are spatially homogeneous (see Chap. 5 of Volume 2). Since 1882, Bianchi was internal professor at the Scuola Normale and in 1886 he won the competition for the chair of Projective Geometry at University of Pisa, where he was full-professor for the rest of his life. The same year he published the first edition of his Lezioni di Geometria Differenziale, which is the very first comprehensive treaty on the new discipline pioneered by Riemann and also the first place where the name Differential Geometry appeared.

Bianchi died in 1928 and he is buried in the Cimitero Monumentale, Piazza dei Miracoli of Pisa. Since the later 1880s up to the end of his life he was an extremely prominent and influential mathematician of the then flourishing Italian School of Geometry. In 1904 Bianchi was member of the committee appointed by the Accademia Nazionale dei Lincei to select the winning paper for the 1901 Royal Prize of Mathematics. Ricci’s ambitions on that Prize had already been manifested some years before, when he presented his works to the committee then headed by Eugenio Beltrami. Notwithstanding Beltrami’s very favorable impressions, the final verdict of the jury on the relevance of tensor analysis had been hesitating and the Prize had not been attributed. Similar conclusion obtained the competition of 1904. Luigi Bianchi showed a great appreciation for the mathematical soundness and vastity of Ricci’s methods but concluded that tensor analysis had not yet demonstrated its relevance and essentiality. He utilized Kronecker’s words to say that he preferred new results found with old methods rather than old results retrieved with new, although very powerful, techniques. These events are quite surprising in view of the fact that two years before, in 1902, Bianchi had published his paper containing those identities on the Ricci tensor for which his name is mostly remembered.

The Royal Prize for Mathematics, denied to Ricci Curbastro, was attributed few years later, in the 1907 edition, to Ricci’s former student Tullio Levi Civita, by a committee that once again included Luigi Bianchi, together with other distinguished mathematicians such as Vito Volterra and Corrado Segre. This time the usefulness of the tensor methods had been made absolutely undoubtable by the vastity of Levi Civita’s results.

Although a little bit dismayed by the failure to get the Royal Prize, Ricci Curbastro ended his life in 1925 surrounded by the appreciation of his colleagues and of his fellow citizens both as a scientist and as a politician. Indeed he was nominated member of several academies, including the most prestigious one, that of Lincei and also occupied positions in the local administration of his native city, Lugo di Romagna. On the contrary his genial student Levi Civita, who was professor at the University of Rome La Sapienza, notwithstanding the Royal Prize and other honors, suffered, under the fascist racial laws of 1938, the removal from his chair because of his Jewish origin. Depressed and completely isolated from the scientific world he died from sorrow in 1941.