
- •Preface
- •Acknowledgements
- •Contents
- •1.1 Introduction
- •1.2 Classical Physics Between the End of the XIX and the Dawn of the XX Century
- •1.2.1 Maxwell Equations
- •1.2.2 Luminiferous Aether and the Michelson Morley Experiment
- •1.2.3 Maxwell Equations and Lorentz Transformations
- •1.3 The Principle of Special Relativity
- •1.3.1 Minkowski Space
- •1.4 Mathematical Definition of the Lorentz Group
- •1.4.1 The Lorentz Lie Algebra and Its Generators
- •1.4.2 Retrieving Special Lorentz Transformations
- •1.5 Representations of the Lorentz Group
- •1.5.1 The Fundamental Spinor Representation
- •1.6 Lorentz Covariant Field Theories and the Little Group
- •1.8 Criticism of Special Relativity: Opening the Road to General Relativity
- •References
- •2.1 Introduction
- •2.2 Differentiable Manifolds
- •2.2.1 Homeomorphisms and the Definition of Manifolds
- •2.2.2 Functions on Manifolds
- •2.2.3 Germs of Smooth Functions
- •2.3 Tangent and Cotangent Spaces
- •2.4 Fibre Bundles
- •2.5 Tangent and Cotangent Bundles
- •2.5.1 Sections of a Bundle
- •2.5.2 The Lie Algebra of Vector Fields
- •2.5.3 The Cotangent Bundle and Differential Forms
- •2.5.4 Differential k-Forms
- •2.5.4.1 Exterior Forms
- •2.5.4.2 Exterior Differential Forms
- •2.6 Homotopy, Homology and Cohomology
- •2.6.1 Homotopy
- •2.6.2 Homology
- •2.6.3 Homology and Cohomology Groups: General Construction
- •2.6.4 Relation Between Homotopy and Homology
- •References
- •3.1 Introduction
- •3.2 A Historical Outline
- •3.2.1 Gauss Introduces Intrinsic Geometry and Curvilinear Coordinates
- •3.2.3 Parallel Transport and Connections
- •3.2.4 The Metric Connection and Tensor Calculus from Christoffel to Einstein, via Ricci and Levi Civita
- •3.2.5 Mobiles Frames from Frenet and Serret to Cartan
- •3.3 Connections on Principal Bundles: The Mathematical Definition
- •3.3.1 Mathematical Preliminaries on Lie Groups
- •3.3.1.1 Left-/Right-Invariant Vector Fields
- •3.3.1.2 Maurer-Cartan Forms on Lie Group Manifolds
- •3.3.1.3 Maurer Cartan Equations
- •3.3.2 Ehresmann Connections on a Principle Fibre Bundle
- •3.3.2.1 The Connection One-Form
- •Gauge Transformations
- •Horizontal Vector Fields and Covariant Derivatives
- •3.4 Connections on a Vector Bundle
- •3.5 An Illustrative Example of Fibre-Bundle and Connection
- •3.5.1 The Magnetic Monopole and the Hopf Fibration of S3
- •The U(1)-Connection of the Dirac Magnetic Monopole
- •3.6.1 Signatures
- •3.7 The Levi Civita Connection
- •3.7.1 Affine Connections
- •3.7.2 Curvature and Torsion of an Affine Connection
- •Torsion and Torsionless Connections
- •The Levi Civita Metric Connection
- •3.8 Geodesics
- •3.9 Geodesics in Lorentzian and Riemannian Manifolds: Two Simple Examples
- •3.9.1 The Lorentzian Example of dS2
- •3.9.1.1 Null Geodesics
- •3.9.1.2 Time-Like Geodesics
- •3.9.1.3 Space-Like Geodesics
- •References
- •4.1 Introduction
- •4.2 Keplerian Motions in Newtonian Mechanics
- •4.3 The Orbit Equations of a Massive Particle in Schwarzschild Geometry
- •4.3.1 Extrema of the Effective Potential and Circular Orbits
- •Minimum and Maximum
- •Energy of a Particle in a Circular Orbit
- •4.4 The Periastron Advance of Planets or Stars
- •4.4.1 Perturbative Treatment of the Periastron Advance
- •References
- •5.1 Introduction
- •5.2 Locally Inertial Frames and the Vielbein Formalism
- •5.2.1 The Vielbein
- •5.2.2 The Spin-Connection
- •5.2.3 The Poincaré Bundle
- •5.3 The Structure of Classical Electrodynamics and Yang-Mills Theories
- •5.3.1 Hodge Duality
- •5.3.2 Geometrical Rewriting of the Gauge Action
- •5.3.3 Yang-Mills Theory in Vielbein Formalism
- •5.4 Soldering of the Lorentz Bundle to the Tangent Bundle
- •5.4.1 Gravitational Coupling of Spinorial Fields
- •5.5 Einstein Field Equations
- •5.6 The Action of Gravity
- •5.6.1 Torsion Equation
- •5.6.1.1 Torsionful Connections
- •The Torsion of Dirac Fields
- •Dilaton Torsion
- •5.6.2 The Einstein Equation
- •5.6.4 Examples of Stress-Energy-Tensors
- •The Stress-Energy Tensor of the Yang-Mills Field
- •The Stress-Energy Tensor of a Scalar Field
- •5.7 Weak Field Limit of Einstein Equations
- •5.7.1 Gauge Fixing
- •5.7.2 The Spin of the Graviton
- •5.8 The Bottom-Up Approach, or Gravity à la Feynmann
- •5.9 Retrieving the Schwarzschild Metric from Einstein Equations
- •References
- •6.1 Introduction and Historical Outline
- •6.2 The Stress Energy Tensor of a Perfect Fluid
- •6.3 Interior Solutions and the Stellar Equilibrium Equation
- •6.3.1 Integration of the Pressure Equation in the Case of Uniform Density
- •6.3.1.1 Solution in the Newtonian Case
- •6.3.1.2 Integration of the Relativistic Pressure Equation
- •6.3.2 The Central Pressure of a Relativistic Star
- •6.4 The Chandrasekhar Mass-Limit
- •6.4.1.1 Idealized Models of White Dwarfs and Neutron Stars
- •White Dwarfs
- •Neutron Stars
- •6.4.2 The Equilibrium Equation
- •6.4.3 Polytropes and the Chandrasekhar Mass
- •6.5 Conclusive Remarks on Stellar Equilibrium
- •References
- •7.1 Introduction
- •7.1.1 The Idea of GW Detectors
- •7.1.2 The Arecibo Radio Telescope
- •7.1.2.1 Discovery of the Crab Pulsar
- •7.1.2.2 The 1974 Discovery of the Binary System PSR1913+16
- •7.1.3 The Coalescence of Binaries and the Interferometer Detectors
- •7.2 Green Functions
- •7.2.1 The Laplace Operator and Potential Theory
- •7.2.2 The Relativistic Propagators
- •7.2.2.1 The Retarded Potential
- •7.3 Emission of Gravitational Waves
- •7.3.1 The Stress Energy 3-Form of the Gravitational Field
- •7.3.2 Energy and Momentum of a Plane Gravitational Wave
- •7.3.2.1 Calculation of the Spin Connection
- •7.3.3 Multipolar Expansion of the Perturbation
- •7.3.3.1 Multipolar Expansion
- •7.3.4 Energy Loss by Quadrupole Radiation
- •7.3.4.1 Integration on Solid Angles
- •7.4 Quadruple Radiation from the Binary Pulsar System
- •7.4.1 Keplerian Parameters of a Binary Star System
- •7.4.2 Shrinking of the Orbit and Gravitational Waves
- •7.4.2.1 Calculation of the Moment of Inertia Tensor
- •7.4.3 The Fate of the Binary System
- •7.4.4 The Double Pulsar
- •7.5 Conclusive Remarks on Gravitational Waves
- •References
- •Appendix A: Spinors and Gamma Matrix Algebra
- •A.2 The Clifford Algebra
- •A.2.1 Even Dimensions
- •A.2.2 Odd Dimensions
- •A.3 The Charge Conjugation Matrix
- •A.4 Majorana, Weyl and Majorana-Weyl Spinors
- •Appendix B: Mathematica Packages
- •B.1 Periastropack
- •Programme
- •Main Programme Periastro
- •Subroutine Perihelkep
- •Subroutine Perihelgr
- •Examples
- •B.2 Metrigravpack
- •Metric Gravity
- •Routines: Metrigrav
- •Mainmetric
- •Metricresume
- •Routine Metrigrav
- •Calculation of the Ricci Tensor of the Reissner Nordstrom Metric Using Metrigrav
- •Index

2.6 Homotopy, Homology and Cohomology |
75 |
Fig. 2.24 The continuous map the realizes
the homotopy between the constant loop and the
product of any loop with its own inverse
Definition 2.6.3 A differentiable manifold M which is arc-wise connected is named simply connected if its fundamental group π1(M ) is the trivial group composed only by the identity element.
π1(M ) = id M = simply connected |
(2.6.16) |
2.6.2 Homology
The notion of homotopy led us to introduce an internal composition group for paths, the fundamental group π1(M ), whose structure is a topological invariant of the manifold M , since it does not change under continuous deformations of the latter. For this group we have used a multiplicative notations since nothing guarantees a priori that it should be Abelian. Generically the fundamental homotopy group of a manifold is non-Abelian. As mentioned above there are higher homotopy groups πn(M ) whose elements are the homotopy classes of Sn spheres drawn on the manifold.
In this section we turn our attention to another series of groups that also codify topological properties of the manifold and are on the contrary all Abelian. These are the homology groups:
Hk (M ); k = 0, 1, 2, . . . , dim(M ) |
(2.6.17) |
We can grasp the notion of homology if we persuade ourselves that it makes sense to consider linear combinations of submanifolds or regions of dimension p of
76 |
2 Manifolds and Fibre Bundles |
Fig. 2.25 The standard
p-simplexes for p = 0, 1, 2
a manifold M , with coefficients in a ring R that can be either Z, or R or, sometimes Zn. The reason is that the submanifolds of dimension p are just fit to integrate p-differential forms over them. This fact allows to give a meaning to an expression of the following form:
C (p) = m1S1(p) + m2S2(p) + · · · + mk Sk(p) |
(2.6.18) |
where Si(p) M are suitable p-dimensional submanifolds of the manifold M , later
on called simplexes, and mi R are elements of the chosen ring of |
coefficients. |
|||||||||||||
|
(p) |
|
||||||||||||
What we systematically do is the following. For each differential p-form ω |
|
|||||||||||||
Λp (M ) we set: |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ω(p) |
|
|
|
|
|
|
ω(p) |
k |
mi |
ω(p) |
(2.6.19) |
||
C |
(p) |
= |
|
(p) |
(p) |
(p) |
C |
(p) |
|
|
(p) |
|
|
|
|
|
m1S1 |
+m2S2 |
+···+mk Sk |
|
= i 1 |
|
Si |
|
|
|
|||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
and in this we define the integral of ω(p) on the region C (p). Next let us give the precise definition of the p-simplexes of which we want to take linear combinations.
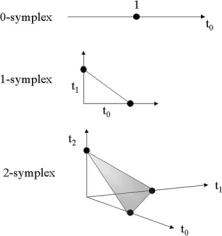
Definition 2.6.4 Let us consider the Euclidian space Rp+1. The standard p-simplex p is the set of all points {t0, t1, . . . , tp } Rp+1 such that the following conditions
are satisfied:
ti ≥ 0; t0 + t1 + · · · + tp = 1 |
(2.6.20) |
It is just easy to see that the standard 0-simplex is a point, namely t0 = 1, the standard 1-simplex is a segment of line, the standard 2-simplex is a triangle, the standard 3-simplex is a tetrahedron and so on (see Fig. 2.25).

2.6 Homotopy, Homology and Cohomology |
77 |
Fig. 2.26 The faces of the standard 1-simplex
Fig. 2.27 The faces of the standard 2-simplex
Let us now consider the standard (p − 1)-simplex (p−1) and let us observe that
there are (p + 1) canonical maps φi that map |
(p−1) into p : |
|
|
||||
|
|
|
|
φi : (p−1) → |
p |
(2.6.21) |
|
These maps are defined as follows: |
|
|
|
||||
φi(p)(t0, . . . , ti−1, ti+1, . . . , tp ) = (t0, . . . , ti−1, 0, ti+1, . . . , tp ) |
(2.6.22) |
||||||
|
p |
|
+ |
1 standard simplexes |
|
p |
|
Definition 2.6.5 The p |
|
p−1 immersed in the standard p- |
|||||
simplex |
|
by means of the p + 1 maps of (2.6.22) are named the faces of |
|
and |
|||
the index i enumerates them. Hence the map φi(p) yields, as a result, the ith face of the standard p-simplex.
For instance the two faces of the standard 1-simplex are the two points (t0 = 0, t1 = 1) and (t0 = 1, t1 = 0) as shown in Fig. 2.26.
Similarly the three segments (t0 = 0, t1 = t, t2 = 1− t), (t0 = t, t1 = 0, t2 = 1− t) and (t0 = t, t1 = 1 − t, t2 = 0) are the three faces of the standard 2-simplex (see Fig. 2.27).
Definition 2.6.6 Let M be a differentiable manifold of dimension m. A continuous map:
σ (p) : (p) → M |
(2.6.23) |
of the standard p-simplex into the manifold is named a singular p-simplex or simply a simplex of M .

78 |
2 Manifolds and Fibre Bundles |
Fig. 2.28 S1(2) and S2(2) are two distinct 2-simplexes, namely two triangles with vertices respectively given by
(A0, A1, A2) and B0, B1, B2. The 2-simplex S3(2) with vertices B0, A1, A2 is the
intersection of the other two
S3(2) = S1(2) " S2(2)
Clearly a 1-simplex is a continuous path in M , a 2-simplex is a portion of surface immersed M and so on. The ith face of the simplex σ (p) is given by the (p − 1)-
simplex obtained by composing σ (p) with φi :
σ (p) ◦ φi : (p−1) → M |
(2.6.24) |
Let R be a commutative ring.
Definition 2.6.7 Let M be a manifold of dimension m. For each 0 ≤ n ≤ m the group of n-chains with coefficients in R, named C(M , R), is defined as the free R-module having a generator for each n-simplex in M .
In simple words Definition 2.6.7 states that Cp(M , R) is the set of all possible linear combination of p-simplexes with coefficients in R:
C (p) = m1S1(p) + m2S2(p) + · · · + mk Sk(p) |
(2.6.25) |
where mi R. The elements of Cp (M , R) are named p-chains.
The concept of p-chains gives a rigorous meaning to the intuitive idea that any p-dimensional region of a manifold can be constructed by gluing together a certain number of simplexes. For instance a path γ can be constructed gluing together a finite number of segments (better their homeomorphic images). In the case p = 2, the construction of a two-dimensional region by means of 2-simplexes corresponds to a triangulation of a surface.
As an example consider the case where the manifold we deal with is just the complex plane M = C and let us focus on the 2-simplexes drawn in Fig. 2.28.
The chain: |
|
C (2) = S1(2) + S2(2) |
(2.6.26) |
denotes the region of the complex plane depicted in Fig. 2.29, with the proviso that when we compute the integral of any 2-form on C (2) the contribution from the simplex S3(2) = S1(2) " S2(2) (the shadowed area in Fig. 2.29) has to be counted twice
since it belongs both to S1(2) and to S2(2).
Relying on these notions we can introduce the boundary operator.

2.6 Homotopy, Homology and Cohomology |
79 |
Fig. 2.29 Geometrically the chain S1(2) + S2(2) is the union of the two simplexes
S1(2) S2(2)
Definition 2.6.8 The boundary operator ∂ is the map: |
|
∂ : Cn(M , R) → Cn−1(M , R) |
(2.6.27) |
defined by the following properties: |
|
1. R-linearity |
|
C1(p), C2(p) Cp (M , R), m1, m2 R |
(2.6.28) |
∂m1C1(p) + m2C2(p) = m1∂C1(p) + m2∂C2(p)
2.Action on the simplexes
∂σ ≡ σ ◦ φ0 − σ ◦ φ1 + σ ◦ φ1 − · · ·
p |
|
= (−)i σ ◦ φi |
(2.6.29) |
i=1 |
|
The image of a chain C through ∂, namely ∂C , is called the boundary of the chain.
As an exercise we can compute the boundary of the 2-chain C (2) = S1(2) + S2(2) of Fig. 2.28, with the understanding that the relevant ring is, in this case Z. We have:
|
∂C(2) = ∂S1(2) + ∂S2(2) |
|
A A |
|
B B |
|
|
B B |
|
|
B B |
(2.6.30) |
|||
|
|
A A |
A A |
|
|
|
|
|
|
||||||
|
= |
−−−→ |
−−−→ |
+ |
−−−→ |
+ |
−−−→ |
− |
−−−→ |
+ |
−−−→ |
|
|||
|
1 2 − |
0 2 |
0 1 |
1 2 |
0 2 |
1 2 |
|
||||||||
where A A |
, . . . denote the oriented segments from A |
1 |
to A |
2 |
and so on. As one sees |
||||||||||
−−−1 →2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
the change in sign is interpreted as the change of orientation (which is the correct interpretation if one thinks of the chain and of its boundary as the support of an integral). With this convention the 1-chain:
−−−→ |
− |
−−−→ |
+ |
−−−→ |
= |
−−−→ |
+ |
−−−→ |
+ |
−−−→ |
(2.6.31) |
|||||||||||
A A |
2 |
A |
A |
2 |
A |
A |
1 |
A |
A |
2 |
A |
A |
0 |
A |
A |
1 |
||||||
1 |
0 |
|
0 |
|
1 |
|
2 |
|
0 |
|
|
|||||||||||
is just the oriented boundary of the S1(2)-simplex as shown in Fig. 2.30.
Theorem 2.6.3 The boundary operator ∂ is nilpotent, namely it is true that:
∂2 ≡ ∂ ◦ ∂ = 0 |
(2.6.32) |

80 |
2 Manifolds and Fibre Bundles |
Fig. 2.30 The oriented boundary of the S(2) symplex
Proof It is sufficient to observe that, as a consequence of their own definition, the maps φi defined in (2.6.22) have the following property:
(p) |
(p−1) |
(p) |
(p−1) |
(2.6.33) |
φi |
◦ φj |
= φj |
◦ φi−1 |
Then, for the p-simplex σ we have:
p
∂∂σ = (−)i δ[σ ◦ φi ]
i=0
pp−1
=(−)i (−)j σ ◦ φi(p) ◦ φj(p−1)
i=0 j =0 |
|
|
|
|
|
|
|
|
|
|
p |
( )i+j σ |
|
|
φi(p−1 |
1) |
|
p−1 |
|
φj(p−1) |
|
|
φj(p) |
◦ |
+ |
σ φi(p) |
◦ |
(2.6.34) |
||||
= |
− |
◦ |
− |
|
|
|
|
|||
j <i=1 |
|
|
|
|
|
|
0=i≤j |
|
|
|
We can verify that everything in the last line of (2.6.34) cancels identically and this
proves the theorem. |
|
|
As an illustration we can calculate ∂∂S1(2) for the |
2-simplex S1(2) described in |
|
Fig. 2.28. We obtain: |
|
|
∂∂S1(2) = A2 − A1 − A2 + A0 + A1 |
− A0 = 0 |
(2.6.35) |
The nilpotency of the boundary operator ∂ that acts on the chains is the counterpart of the nilpotency of the exterior derivative d that acts on differential forms as explained in Sect. 2.5.4. Consider Fig. 2.31. As one sees the sequence of the vector spaces Cm of m-chains can be put into correspondence with the sequence of vector spaces Λm of differential m-forms.
The operator:
∂ : Ck → Ck−1 |
(2.6.36) |
makes you to travel on the sequence from left to right, while the exterior derivative operator:
d : Λk → Λk+1 |
(2.6.37) |
causes you to travel along the same sequence in the opposite direction from right to left. Both ∂ and d are nilpotent maps.
