2.Уравнения электростатического поля в интегральной и дифференциальной форме

Интегральная форма уравнений описывает поле в конечных размерах объема, поверх­ности, линии, расположенных в пространстве. Дифференциаль­ная форма тех же уравнений описывает поле в произвольных точках простран­ства.

1.Закон Кулона определяет силу взаимодействия между двумя точечными зарядами:

.

Сила взаимодействия двух точечных зарядов направлена по прямой, со­единяющих эти заряды, при этом одноименные заряды отталкиваются, а разно­именные  притягиваются.

2.Ранее была получена интегральная форма уравнения циркуляции век­тора напряжен­ности поля по замкнутому контуру:

интегральная форма.

По теореме Стокса перейдем к дифференциальной форме этого уравне­ния:

.

Так как площадка выбиралась произвольно, то очевидно проекция век­торана любое направление равна нулю, следовательно и сам вектор равен нулю:

дифференциальная форма.

Ротор вектора характеризует его вихри в пространстве. Равенствоозна­чает, что электростатическое поле является безвихревым, т.е. по­тенциальным.

В декартовой системе координат операция rot запишется так:

.

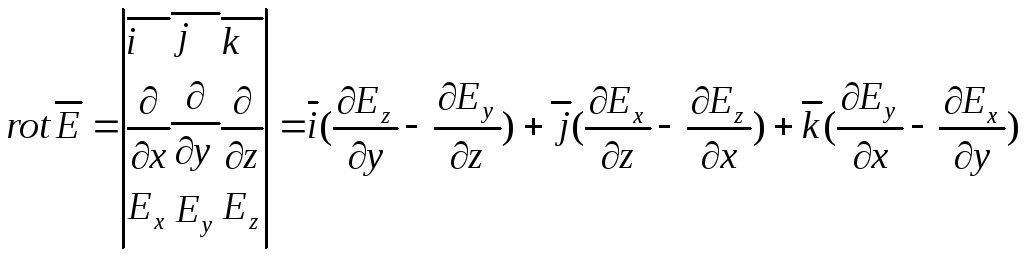3. Теорема Гаусса является одной из фундаментальных теорем в теории поля:

интегральная форма записи теоремы гласит, что поток вектора элек­трического смещения сквозь замкнутую поверхностьS равен ал­гебраической сумме сво­бодных зарядов, расположенные внутри поверхности S.

Для однородной среды , тогда.

По теореме Остроградского перейдем к дифференциальной форме урав­нения теоремы Гаусса:

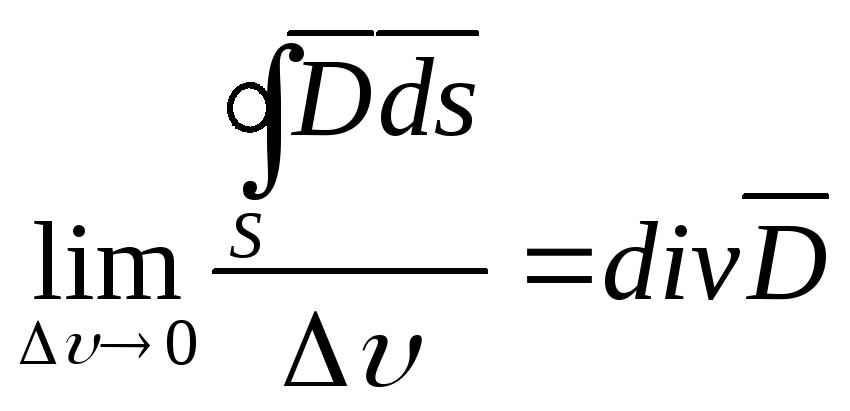, , следовательно:

―дифференциальная форма.

Дивергенция вектора характеризует его истоки в пространстве, следо­вательно, ли­нии вектораначинаются на положительных зарядах и заканчи- ваются на отрицательных.

В декартовой системе координат операция div запишется так:

.

Для однородной среды , тогда.

4. Электростатическое поле обладает способностью запасать энергию. Объемная плотность этой энергии выражается уравнением:

[Дж/м³].

Для определения запаса энергии в заданном обьеме v необходимо выполнить интегрирование плотности энергии по заданному обьему:

.

3. Граничные условия в электростатическом поле

Выделим произвольную точку n, расположенную в электростатическом поле на по­верхности раздела двух диэлектриков с разными значениями диэлек­трической проницаемо­сти и(рис. 3)

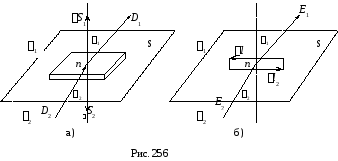
Окружим точку n элементарной призмой, у которой высота бесконечно мала по срав­нению с линейными размерами основания. Применим к поверхно­сти призмы теорему Гаусса, при этом пренебрежем потоком вектора через боковые поверхности ввиду их малости. Тогда получим:

, или

, .

На границе раздела двух диэлектриков равны нормальные составляющие вектора электрического смещения .

Окружим выделенную точку n элементарным прямоугольником, высота которого бес­конечно мала по сравнению с его длиной (рис. 256б). Найдем значе­ние циркуляции вектора по периметру прямоугольника:

, или

, .

На границе раздела двух диэлектриков равны тангенциальные состав­ляющие вектора напряженности поля .

Разделим почленно вторые уравнения на первые и учтем, что , получим

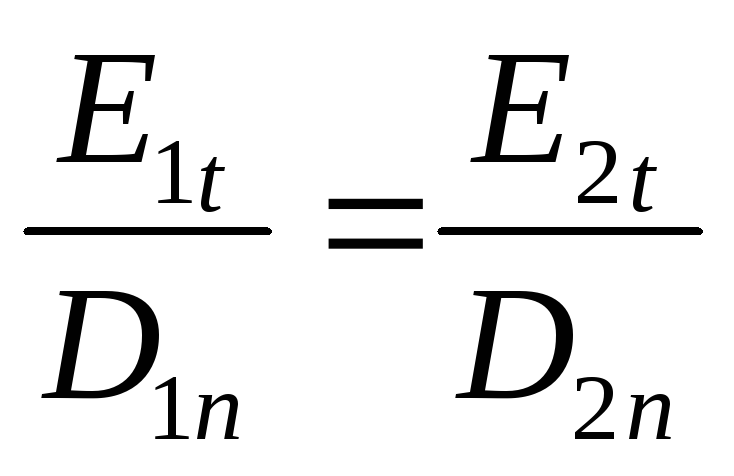или , откуда следует

―условие преломления линий поля на поверхности раздела двух диэлек­триков с различными значениями и диэлектрической проницаемо­сти(и).

Если линии поля направлены нормально к поверхности раздела (), то

, .

Рассмотрим граничные условия на поверхности раздела диэлектрика с проводником.

Электрическое поле внутри проводника отсутствует (= 0), а его поверх­ность явля­ется эквипотенциальной. На поверхности проводника бесконечно тонким слоем будут распо­лагаться свободные разряды с поверхностной плотно­стью. Лини поля в диэлектрике будут направлены нормально к поверхности проводника как к эквипотенциальной поверхности. Применяя рассуждения, аналогичные предыдущему примеру, получим:

, .