8. Переходные процессы в линии с распределенными параметрами

В цепях с сосредоточенными параметрами переходные процессы проте­кают одно­временно во всех направлениях цепи с одинаковой скоростью затуха­ния.

В цепях с распределенными параметрами переходной процесс, начав­шийся в какой-либо точке цепи, распространяется на остальные элементы в виде волн, которые распро­страняются вдоль цепи с конечной скоростью v. Эта скорость близка к скорости света км/c в воздушных линиях иv<c для кабельных линий. По мере распространения вдоль линии волна изменяет свою форму, поэтому переходной процесс в разных точках ли­нии выглядит по-раз­ному. Таким образом, переходной процесс в цепи с распределенными парамет­рами протекает в функции двух переменных – пространства и время.

В высоковольтных линиях электропередачи переходные процессы возни­кают при раз­личных коммутациях, а так же от грозовых явлений в атмосфере. При переходом процессе на отдельных участках линии могут возникнуть пере­напряжения, нередко приводящие к пробою изоляции, или большие токи, вызы­вающие механические разрушения конструкций. Умение рассчитывать эти пе­ренапряжения и сверхтоки необходимы в инженерной практике для правиль­ного выбора и расчета отдельных частей электроустановок.

Анализ переходных процессов в линии с распределёнными параметрами проводится на основе решения ее дифференциальных уравнений, полученных ранее:

.

Решение дифференциальных уравнений в частных производных в общем случае представляет сложную математическую задачу, решение которой выхо­дит за рамки учеб­ного курса ТОЭ. Поэтому здесь ограничимся рассмотрением частного случая линии без по­терь, т.е. при условии ,.

Дифференциальные уравнения линии без потерь получат вид:

;

.

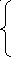Выполним решение этой системы дифференциальных уравнений, для чего каждое из уравнений продифференцируем сначала по переменной х, а потом по переменной t:

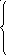
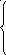
Совместное решение каждой пары полученных уравнений дает результат:

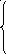
Введем обозначение  скорость волны, после чего уравнения примут вид:

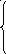
В курсе математики уравнения данного вида получили название волно­вых, и им со­ответствует следующие решения (без вывода):

,

.

9. Расчет падающих волн в линии с распределенными параметрами при подключении ее к источнику эдс

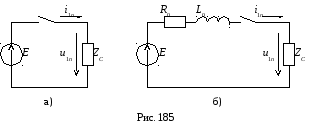
Пусть линия с волновым сопротивлением в моментt = 0 под­ключается к источнику ЭДС илис нулевыми или с ненулевыми внутренними параметрами. Источник ЭДС восприни­мает линию как волновое сопро­тивление, поэтому эквивалентная схема цепи для расчета режима в начале линии будет иметь вид рис. 185 а, б:

Рассмотрим различные варианты форм падающих волн в зависимости от параметров источника ЭДС.

1. Источник постоянной ЭДС e(t) = E с нулевыми внутренними парамет­рами 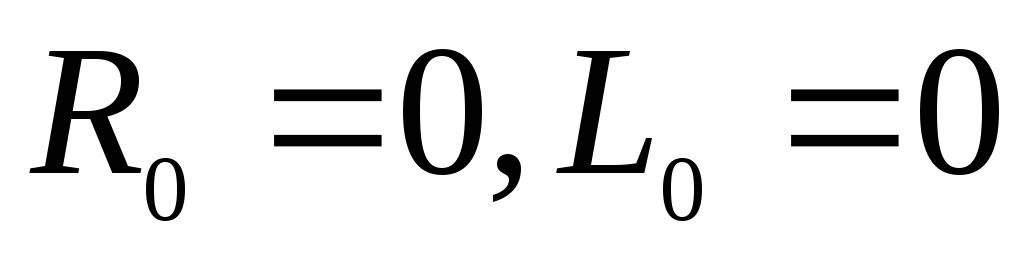( рис. 185а ).

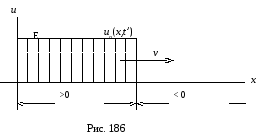
После замыкания рубильника в момент t=0 возникнут падающие волны с прямоуголь­ным фронтом: . Фронтом волны называется ее началь­ный участок. Во всех точках линии, пройденных фронтом волны, устанавливается постоян­ный режим (),u(t)=E, . Для точек линии, куда фронт не дошел (),u=0 и i=0 (рис. 186). Так как формы падающих волн иидентичны, то на гра­фической диаграмме рис. 186 изображена только падающая волна напряжения.

2. Источник синусоидальной ЭДС 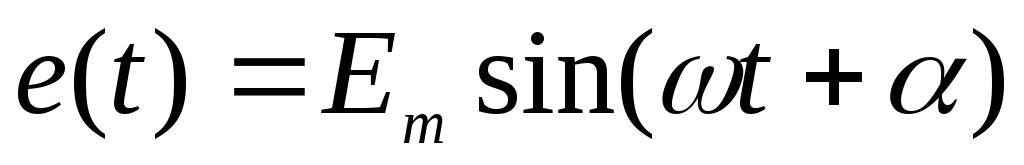с нулевыми внут­ренними па­раметрами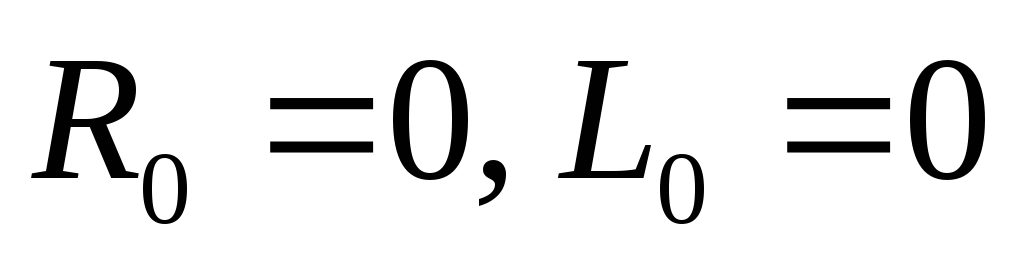(рис. 1а).

Напряжение и ток в начале линии после замыкания рубильника устано­вятся мгно­венно и будут равны:

, .

Фронт волны будет определяться начальной фазой в момент времени включенияt = 0;. С течением времени волны будут распространяться вдоль линии. Дли их математического выражения заменим в предыдущих урав­нениях переменнуюt на :

,

.

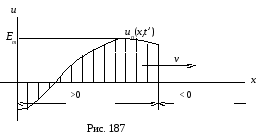
Как и в предыдущем случае, решение справедливо при условии . Из решения следует, что падающие волныираспределяются вдоль линии по синусои­дальному закону (рис. 187).

3. Источник постоянной ЭДС e(t)=Е с параметрами 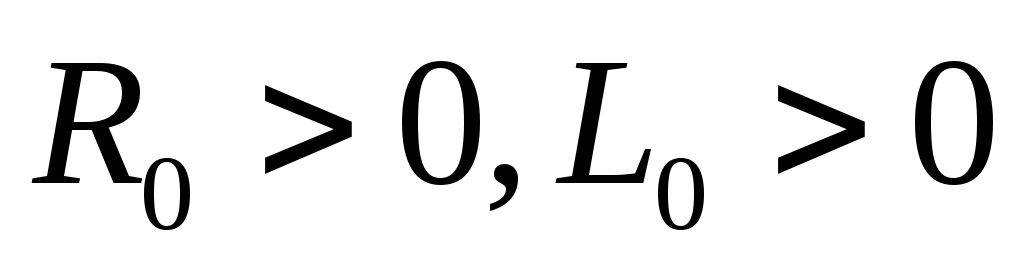(рис. 1б).

Напряжение и ток в начале линии после замыкания рубильнику опреде­лятся путем расчета переходного процесса в схеме замещения (рис. 1б) класси­ческим или операторным методом:

, ,

где  корень характеристического уравнения.

Для математического выражения волн в линии заменим переменную t на :

, .

Полученные решения справедливы при условии . Из решения следует, что па­дающие волныиизменяются во времени и про­странстве по экспоненциаль­ному закону (рис. 188а, б).

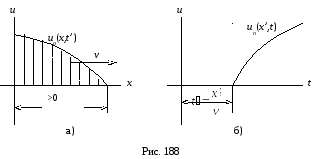
Таким образом, для расчета падающих волн в линии ,необходимо выполнить расчет переходного процесса в схеме замещения для начала линии и в получен­ных выражениях заменить переменнуюt на .