8.4. Асимптотические последовательности и асимптотические разложения

Ранее для оценки скорости изменения функций были введены калибровочные функции. Вместе с тем для асимптотического представления заданной функции не обязательно ограничиваться перечисленными функциями сравнения. Вместо них можно использовать произвольную последовательность функций общего вида , удовлетворяющих условию

при . (8.11)

Определение. Последовательность функций , удовлетворяющих условию (8.11) называется асимптотической последовательностью. Через асимптотическую последовательность можно определить и асимптотическое разложение.

Определение. Сумма вида , где не зависит от , а представляет собой асимптотическую последовательность, называется асимптотическим разложением функции , если при

(8.12)

или, что, то же самое,

. (8.13)

Этот факт записывается в виде

при .

Отметим, что функция может быть представлена бесконечным числом асимптотических разложений.

При построении приближенных решений различного вида уравнений, а также при оценке интегралов предполагается обычно, что такие разложения можно подставлять в уравнения и выполнять арифметические действия, а также дифференцирование и интегрирование. Иногда применение некоторых из этих операций необоснованно. В этом случае они приводят к сингулярностям или неравномерностям.

Пример. Равенство

не обоснованно при , т.к. второй, третий и последующие члены разложения сравнимы по порядку величины с первым членом. Поэтому ошибка, совершаемая при усечении ряда после членов при не будет иметь порядок , т.е. не будет порядка первого отброшенного члена. В этом случае говорят о неравномерном разложении. Одна из главных целей метода возмущений проверка равномерности разложения.

Задачи для самостоятельного решения.

1. Определить первые три члена разложения при малом :

2. Определить порядок функции при малых :

;

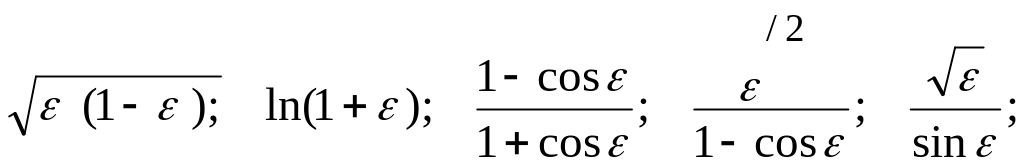
3. Расположить данные выражения в ряд по порядку убывания при малых :

8.5. Простейшие асимптотические методы решения дифференциальных уравнений

Во многих задачах механики колебания консервативных систем с одной степенью свободы описываются дифференциальными уравнениями вида

, (8.14)

где – перемещение, – некоторая нелинейная функция от – восстанавливающая сила, – ускорение. Точками над буквой обозначены производные по времени . Пусть определяет положение равновесия системы. Тогда . Предположим, что функцию в окрестности точки можно разложить в ряд Тейлора

,

где .

Если считать, что восстанавливающая сила является нечетной функцией смещения от равновесия (т.е. пружина ведет себя одинаково при растяжении и сжатии), и ограничиться в разложении функции двумя членами, то уравнение (8.14) примет вид

, (8.15)

где . Уравнение (8.15) обычно называют уравнением Дюффинга.

Введем характерные масштабы задачи – линейный и временной , и перейдем к безразмерным переменным

, .

Используем правило дифференцирование сложной функции для перехода к новым переменным

Тогда уравнение (8.15) преобразуется к виду

.

Введем обозначения , , где и - безразмерные параметры, - характеризует степень нелинейности системы, точка над буквой обозначает дифференцирование по .

Тогда уравнение преобразуется к виду

. (8.16)

В качестве начальных условий примем

, . (8.17)

Прямое разложение. Неравномерность разложения.

Решение уравнения Дюффинга (8.16) отыскиваем в виде ряда по степеням параметра , который считаем малым

. (8.18)

Ограничившись в решении членом правого порядка малости

= , (8.19)

подставим (8.19) в уравнение (8.16) учитывая равенство

Получим

. (8.20)

Полагая в (8.19) имеем уравнение для первого члена разложения (8.18)

. (8.21)

Его решение, как известно, имеет вид

, (8.22)

где и – произвольные постоянные.

Учитывая (8.21), уравнение (8.20) принимает форму

.

Разделим на , а затем положим . Учтя, что и что , получим уравнения для функции

. (8.23)

Отметим, что и уравнение (8.20) и уравнение (8.23) можно получить из (8.20), если приравнять нулю коэффициенты при последовательных степенях .

Подставим в уравнение (8.23) в виде (8.22) и принимая во внимание элементарное равенство

перепишем (8.23) в виде

. (8.24)

Решения соответствующего уравнению (8.24) однородного уравнения имеет вид

(8.25) где и – произвольные постоянные.

В силу линейности уравнения (8.24) частное решение этого неоднородного уравнения можно записать в виде суммы двух частных решений, соответствующих каждому из слагаемых правой части

, (8.26)

. (8.27)

Оба этих уравнения имеют правую часть специального вида. Поэтому частные решения моделируются, а затем применяется метод неопределенных коэффициентов как это показано в курсе дифференциальных уравнений. Для уравнения (8.26) корни характеристического уравнения равны  , поэтому частное решение записывается в виде

.

Подставляя в уравнение (8.26) и применяя метод неопределенных коэффициентов для отыскания А и В, получим

. (8.28)

Аналогично для уравнения (8.27) получим частное решение в виде

. (8.29)

Складывая общее решение однородного уравнения (8.25) и частные решения (8.28) и (8.29) получим общее решение уравнения (8.24) в виде

(8.30)

Подставляя и из (8.22) и (8.30) в разложении (8.19) для общего решения уравнения (8.16) получаем следующее разложение первого порядка

, ) = + )+… , (8.31)

где – произвольные постоянные. Хотя мы получили четыре постоянных, но оказывается, что они связаны между собой и для их нахождения вполне достаточно двух начальных условий. Действительно, подставляя разложение (8.31) в условия (8.17), получаем

.

Приравнивая члены при одинаковых степенях в левой и правой частях этих равенств, получим

(8.32)

. (8.33)

Введя оба равенства (8.32) в квадрат и складывая, имеем

, .

Из этих же равенств можно найти и параметр :

= .

Возведя в квадрат равенства (8.33) и сложив их, получим

а также

Таким образом, все постоянные выражены через две заданные и . Преобразуем выражение для решения уравнения Дюффинга, сложив два первых члена в (8.31). Используя известную тригонометрическую формулу, имеем

где

Подставляя полученные выражения для амплитуды а и фазы , и отбрасывая члены высшего порядка малости по , получим решение уравнения Дюффинга вместо (8.31) в виде

(8.34)

где обозначено

Итак, из (8.34) следует, что в первом приближении искомое решение записывается в виде . А первая поправка к этому решению есть

.

Поправочный член будет мал, как это заранее предполагается, только тогда, когда мало по сравнению с единицей. Если же величина имеет порядок О(1), то поправочный член, содержащий этот множитель, может оказаться даже больше главного члена разложения. Поэтому прямое разложение применимо только для таких времен, при которых выполняется , т.е. для .

Таким образом, можно утверждать, что подобные разложения являются неравномерными по , т.к. при больших временах они становятся непригодными. Члены вида называют вековыми или секулярными членами – термин, возникший в астрономии при описании движения планет.