1.5. Условия представимости функции интегралом Фурье

Если функция кусочно-гладкая на каждом конечном отрезке, абсолютно интегрируема на всей оси, то имеет место формула (1.18). Учитывая формулу

и введя обозначения

(1.19)

формулу (1.18) можно записать в виде

= . (1.20)

Равенство (1.20) аналогично разложению функции в тригонометрический ряд, а выражения (1.19) аналогичны формулам (1.9) для коэффициентов Фурье.

Если функция – четная, то формула

= , A(λ) = ,

называется косинус-преобразование Фурье.

Если функция – нечетная, то

= , B(λ) = ,

называется синус-преобразование Фурье.

1.6. Комплексная форма интеграла Фурье. Преобразование Фурье

В комплексной форме интеграл Фурье имеет вид

(1.21)

Если перезаписать выражение (1.21) следующим образом

и обозначить

, (1.22)

то формула (1.21) примет вид

(1.23)

Функция , определенная формулой (1.22), называется образом Фурье или спектральной характеристикой функции . Переход от к называется преобразованием Фурье.

Восстановление ”оригинала” по образу по формуле (1.23) называется обратным преобразованием Фурье.

Если определена только на полуоси 0  х  , то ее можно продолжить на полуоси -  х  0 четно или нечетно. Тогда для получим два разных представления:

(1.24)

. (1.25)

По определению положим

(1.26)

Тогда согласно (1.24) имеем

(1.27)

Функция называется косинус - образом Фурье функции , заданной на полуоси 0  х , переход от к - косинус - преобразованием Фурье. Восстановление функции по с помощью (1.27) называется обратным косинус - преобразованием Фурье.

Аналогично, вместо (1.25) имеем

(1.28)

(1.29)

где называется синус - образом Фурье функции , заданной на полуоси 0  х  , переход от к по формуле (1.28) называется синус - преобразованием Фурье. Восстановление функции по с помощью (1.29) называется обратным синус - преобразованием Фурье.

Задачи для самостоятельного решения

1. Представить интегралом Фурье функции:

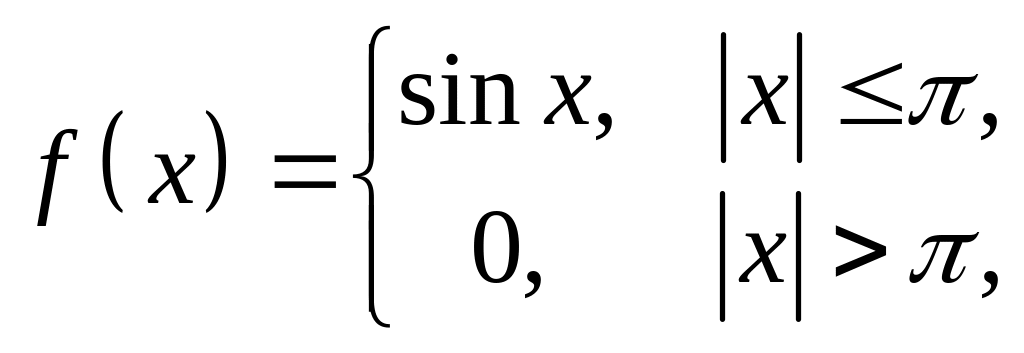
при 0 < x <  продолжив ее

а) четным образом;

б) нечетным образом.

2. Найти преобразование Фурье функции

3. Найти синус- и косинус- преобразования Фурье функции

Литература к п.1.4-1.5. 1, гл.17, §13-14], 2, гл.4. §4.12- 4.14], [4, гл.3, §9].

2. Преобразование Лапласа и его приложения

1. Понятие преобразования Лапласа.

   Свойства преобразования Лапласа

   Функцией-оригиналом будем называть любую действительную функцию действительного переменного t , удовлетворяющую следующим условиям:

1) на любом конечном отрезке положительной полуоси функция удовлетворяет условиям:

ограничена; либо непрерывна, либо имеет конечное число точек разрыва первого рода; имеет конечное число экстремумов;

2) функция =0, если ;

3) функция возрастает не быстрее показательной функции, т.е. существуют такие постоянные , что для всех t

.

Число называется показателем роста функции .

Изображением функции (по Лапласу) называют функцию комплексного переменного , определяемую соотношением

(2.1)

Интеграл (2.1) является несобственным. Область его сходимости является совокупностью тех комплексных чисел , для которых . Тот факт, что функция имеет своим изображением будем записывать символом ÷ .

Простейшей функцией –оригиналом является единичная функция Хевисайда

(2.2)

Умножение функции на придает ей нулевые значения при . В дальнейшем изложении будем предполагать, что все рассматриваемые функции умножены на единичную функцию Хевисайда. Так, например, вместо функции будем писать и так далее.

Пример 1. Найти изображение функции .

Решение. Функция является функцией-оригиналом, так как удовлетворяет условиям, оговоренным в определении. Для нахождения еe изображения нужно вычислить несобственный интеграл

Представим функцию по формуле Эйлера

и подставим в вычисляемый интеграл

= .

Учитывая, что

если , имеем

Результаты вычисления изображений функций с помощью интеграла Лапласа (2.1) составляют таблицу изображений, которая приводится в учебниках (см.[I], гл.XIX, или [2], гл.7).