8. Приближенно-аналитические методы решения дифференциальных уравнений

8.1. Необходимость асимптотических методов

При построении приближенных решений алгебраических, дифференциальных и интегральных уравнений, а также при оценке различных интегралов приходится иметь дело с рядами по степеням параметра или независимой переменной. В разделе “Функциональные ряды и их приложение” рассматриваются решения некоторых дифференциальных уравнений в виде сходящихся степенных рядов.

Среди причин, затрудняющих поиск точного решения физических и инженерных задач, можно указать нелинейность уравнения, наличие переменных коэффициентов, а также нелинейные граничные условия. Для таких задач часто не удается построить решение в виде сходящегося степенного ряда. Обычно в этих случаях используют комбинацию аналитических и численных методов. Из наиболее используемых и мощных аналитических методов можно отметить метод возмущений (асимптотических разложений) по большим или малым значениям координаты или входящего в уравнение параметра.

К асимптотическим методам обращаются в тех случаях, когда пытаются строить решение дифференциального уравнения в виде степенного ряда в окрестности нерегулярной особой точки. Может оказаться, что полученный ряд является всюду расходящимся. Дело в том, что при этом выпадает краеугольный результат теории – утверждение, что в окрестности регулярной особой точки сходятся все степенные ряды.

Пример. Построить решение в виде степенного ряда для дифференциального уравнения

, .

Решение. Вычислим первую и вторую производную

и подставим в дифференциальное уравнение. Имеем

.

Приравнивая нулю коэффициенты при различных степенях , получим:

; ;

; ; … ;

,… .

Отсюда получаем: , – произвольно, ,

, , , …, , … .

Таким образом, получили формальное решение в виде ряда

который расходится при всех , кроме точки .

8.2. Калибровочные функции. Символы порядка

Одним из основных элементов асимптотического анализа является исследование пределов функций при , где . Если предел функции существует, то имеет место одна из альтернатив: при , ; ; , где .

Однако для целей анализа такая классификация слишком груба: существует бесчисленное множество функций, обладающих такими пределами. Для уточнения приведенной классификации каждый из трех указанных классов функций подразделяют в соответствии со скоростью, с которой они стремятся к своим пределам. Поэтому сравнивают скорость убывания или возрастания этих функций с соответствующими характеристиками эталонных функций. Эти функции сравнения называются калибровочными функциями.

Наиболее употребительные из калибровочных функций следующие ( ):

1. Целые положительные степени параметра ;

2. Обратные степени этого параметра: ;

3. Показательные и логарифмические функции: , , , , .

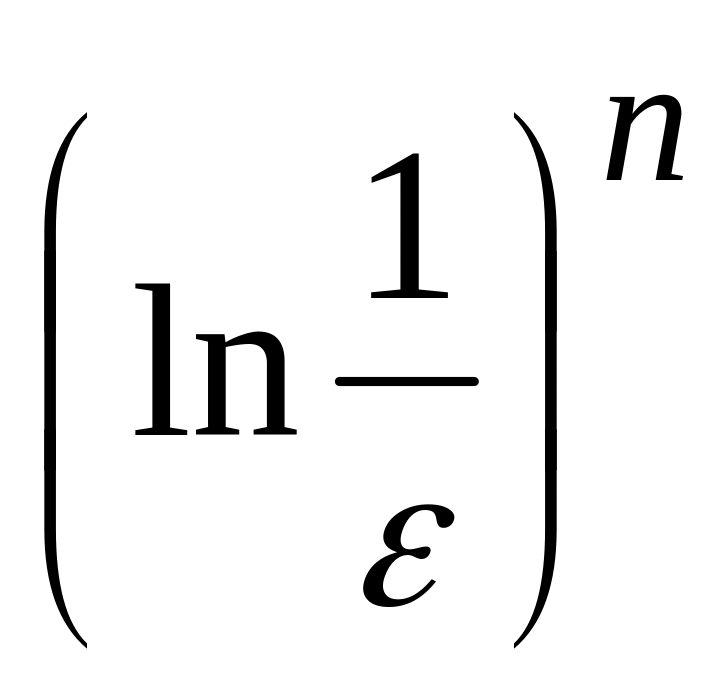Иногда приходится рассматривать и другие калибровочные функции.

Вместо утверждения о том, что c той же скоростью, что и , говорят что « имеет порядок при » и пишут при .

В общем случае полагают при , если существует такое число , что

. (8.1)

Таким образом, при имеют место соответствия:

, , , ,

, , .

Настоятельно рекомендуем проверить все эти равенства.

Введенное с помощью символа « » математическое понятие порядка, формально отличается от физического понятия величин, так как по определению (1) значение постоянной может быть сколь угодно большой, но конечной. Однако обычно принимается, что соответствующий коэффициент порядка единицы и значение, определяемое символом порядка достаточно близко к фактическому значению физической величины.

Помимо введенного символа порядка для характеристики скорости изменения функции относительно калибровочной функции вводится еще один символ определяемый следующим образом

при , если . (8.2)

Рекомендуется проверить следующие соответствия при :

sin , , , , , , .