8.3. Пример асимптотического разложения. Определение асимптотического ряда

Сделаем оценку интеграла при больших

(8.3)

Разложим в степенной ряд множитель при экспоненте в подынтегральной функции. Получаем

(8.4)

Полученный ряд (геометрическая прогрессия) сходится при . Подставим разложение (8.4) в (8.3), найдем

получим

. (8.5)

Для выяснения вопроса о сходимости ряда применим признак Даламбера к ряду (8.5), получим

Следовательно, ряд (8.5) расходится при всех значениях . Получается так, что равенство (8.5) не имеет смысла. С другой стороны, поскольку

то

Далее имеем

Следовательно, интеграл сходится.

Следует заметить, что расходимость ряда (8.5) связана с незаконностью почленного интегрирования ряда (8.4) вне интервала его сходимости.

Однако формулу (8.5) все же можно использовать для вычисления функции после некоторой модификации.

Ограничимся в ряде (8.4) конечным числом членов

и найдем сумму, заметив, что отрезок ряда является геометрической прогрессией

.

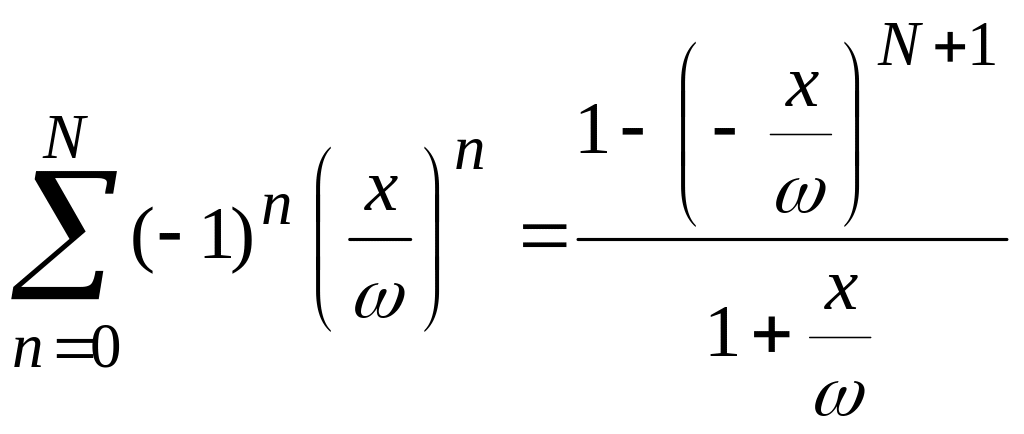Следовательно, можно записать в соответствии с формулой (8.4)

,

где – остаток ряда определяется формулой

= - = = .

Таким образом, формулу (8.4) запишем теперь в виде

= + . (8.6)

Подставим, как и ранее в подынтегральное выражение (8.3), получим

или

, (8.7)

где остаток

. (8.8)

Для сходимости ряда необходимо, чтобы при . Но в нашем случае при в соответствии с признаком Даламбера.

Принципиальный момент заключается в том, что мы зафиксируем номер и оценим величину остатка при . Так как и и , то поэтому из (8.8) получаем

Итак, ошибка, вызванная усечением ряда (8.5) на - ом члене, не превосходит первого отброшенного члена – ( )-го члена. К тому же при фиксированном и  имеем .

Поэтому, хотя ряд (8.5) и расходится, но для фиксированного первые членов ряда приближают функцию c ошибкой, которую можно сделать сколь угодно малой выбором достаточно большого значения .

Такой ряд называется асимптотическим рядом типа Пуанкаре и обозначается .

Определение. Ряд вида , где не зависит от , называется асимптотическим рядом и пишут при  тогда и только тогда, когда

при . (8.9)

Поскольку ,

то условие (8.9) можно записать в виде

при . (8.10)

В заключении отметим, что полезность асимптотических рядов основана на том, что ошибка, получаемая при усечении ряда быстро стремится к нулю при . В вычислениях обычно фиксируют достаточно большое значение параметра и пытаются уменьшить ошибку увеличением числа членов асимптотического ряда. Поскольку ряд расходится, то достигается такое N, за которым добавление новых членов лишь увеличивает ошибку, ведь - конечно. Таким образом, для заданного , существует оптимальное значение N, при котором ошибка минимальна. Практически такое значение N можно отследить, используя ЭВМ.

Для справки приведем практически используемый асимптотический ряд для одной из функций Бесселя

,

причем ряд сходится абсолютно и равномерно при всех значениях х.

при ,

где

,

.

Ряды для и расходятся при всех значениях х.

Для малых х первые несколько членов ряда дают хорошую точность. Например, дают верные 11 значений цифр, если ограничиться девятью членами разложения.

При восемь членов ряда дают точность до 3-й значащей цифры, в то время как такую же точность обеспечивает уже первый член асимптотического разложения.