5.2. Разделение переменных в уравнении Лапласа в декартовой и сферической системах координат

Метод разделения переменных является одним из наиболее употребительных методов решения линейных уравнений в частных производных математической физики. Его использование часто приводит к построению системы ортогональных функций, на базе которой строится решение граничной задачи. Из математической физики известно, что уравнения, содержащие трехмерный оператор Лапласа, допускают разделение переменных в одиннадцати различных системах координат.

Разделение переменных в декартовой системе координат

Уравнение Лапласа в декартовой системе координат имеет вид

. (5.6)

Решение этого уравнения может быть выражено через решения трех обыкновенных дифференциальных уравнений, имеющих одинаковый вид. Разыскиваем решение уравнения (5.6) в виде

. (5.7)

Подставляя (5.7) в (5.6) и деля обе части уравнения на , получим

, (5.8)

где частные производные заменены обыкновенными, поскольку каждая из функций зависит от одной переменной. Чтобы (5.8) было справедливо для произвольных значений аргументов каждое слагаемое должно быть постоянным, т.к. эти слагаемые зависят от разных аргументов

, , ,

(5.9)

где – совершенно произвольны.

Преобразуем отношения в формулах (5.9). Имеем

, (5.10)

Полученные уравнения являются линейными однородными дифференциальными уравнениями с постоянными коэффициентами. Поэтому частные решения каждого из этих уравнений разыскиваем в виде

, , . (5.11)

Подставим эти функции в соответствующие уравнения из (5.10). После стандартной процедуры получаем характеристические уравнения

, ,

и характеристические числа , , . Учитывая эти результаты из формул (5.11) получаем линейно независимые частные решения уравнений (5.10)

, , . (5.12)

В соответствии с формулой (5.7) получим частные решения уравнения Лапласа в виде

, (5.13)

где .

Линейная комбинация решений типа (5.13) позволит получить широкий класс решений уравнения Лапласа.

Решение уравнения Лапласа в форме (5.13) имеет комплексный вид. При решении практических задач, связанных с уравнением Лапласа, иногда целесообразно записывать решение в действительной форме. В этом случае удобно функции (5.12) сразу преобразовать к действительному виду. Для этого вместо первой пары функций в (5.12) введем новые линейно независимые функции, являющиеся линейными комбинациями старых, а именно

,

, (5.14)

, .

Здесь мы для новых функций сохранили старые обозначения Х, Y и Z. Комбинируя в соответствии с формулой (5.7) функции из (5.14), получим частные решения уравнения Лапласа в действительной форме

,

, (5.15)

,

.

Чтобы определить значения X и нужно наложить на функцию определенные граничные условия.

Разделение переменных в сферической системе координат

Используя формулу (5.2) п.5.1, запишем уравнение Лапласа в сферической системе координат

. (5.16)

Подставив в уравнение (5.16) выражение

,

получим 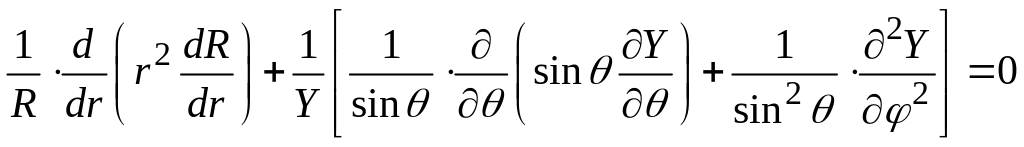. (5.17)

Первое из слагаемых в левой части не зависит от переменных , второе от . Поэтому уравнение удовлетворяется при всех и только тогда, когда каждое из названных слагаемых постоянно, т.е.

,

,

где - постоянная разделения. Отсюда получаем два уравнения, первое из которых является обыкновенным дифференциальным уравнением, а второе – уравнением в частных производных

(5.18)

. (5.19)

Рассмотрим уравнение (5.18) для радиальной функции . Введем новую функцию соотношением: . Вычислим производные

,

и подставим в уравнение (5.18). Получим дифференциальное уравнение для функции

. (5.20)

Упражнение. Проверить, что уравнение (5.20) имеет решения: и , где - произвольное целое число, .

Общее решение уравнения (5.20) имеет вид: . Учитывая этот результат, запишем общее решение уравнения (5.18)

, (5.21)

где постоянные для общности снабжены индексами .

Итак, решив уравнение (5.18), мы также определили вид постоянной разделения - , где - целое число. Рассмотрим теперь уравнение (5.19). Проведем в нем процедуру разделения переменных, разыскивая его решение в виде

, (5.22)

получим

. (5.23)

В уравнении (5.23) от зависит лишь последнее слагаемое, остальные зависят от . Из тех же соображений, что и для уравнения (5.16) , заключаем, что первые два слагаемые в совокупности и третье слагаемое должны быть постоянными. Обозначим эту константу . Получаем дифференциальное уравнение

, (5.24)

решение которого имеет вид , или

, . (5.25)

Для того чтобы была однозначной функцией точки в пространстве, необходимо, чтобы она была периодической функцией от с периодом . Отсюда следует, что постоянная разделения должна принимать целые значения .

Постоянные у функций выбраны из условия нормировки

,

где знак * обозначает комплексные сопряжение.

Оставшаяся часть в (5.23) дает уравнение для определения зависимости от азимутального угла

. (5.26)

Выполним в уравнении (5.26) замену переменной . Тогда

.

Подставив в уравнение (5.26), получим

. (5.27)

Для того чтобы решение имело физический смысл, оно должно быть однозначно, конечно и нейтрально в интервале .

Решение уравнения (5.27) зависит от двух постоянных и . Поэтому его обычно записывают . Уравнение (5.27) называется обобщенным уравнением Лежандра, а его решения – присоединенными функциями Лежандра. При уравнение (5.27) превращается в уравнение полиномов Лежандра, т.е. - полиномы Лежандра (смотри приложение, формулы (5.21) и (5.22)).