Импульсные функции и их приложение к решению дифференциальных уравнений
Во многих практических задачах приходится иметь дело с кратковременными силами (например, ЭДС), имеющими характер мгновенного импульса. Эффект воздействия такой силы часто не зависит от ее вида, а зависит только от ее “площади” и не является малым, если сила достаточно велика.
Такие функции удобно представлять с помощью импульсной функции, называемой дельта – функцией Дирака.
Введем функцию
,
график которой изображен на рисунке 3
Рис. 3
и рассмотрим интеграл
Очевидно, что имеют место следующие равенства
,
.
Если устремлять
к нулю, то получится последовательность
функций
представляющая собой совокупность
прямоугольников одинаковой площади с
уменьшающимися основаниями и возрастающими
высотами. Хотя рассмотренная
последовательность функций и расходится,
вводят условную функцию
,
которую считают пределом этой
последовательности.
Эту условную функцию называют импульсной функцией или дельта – функцией
Для дельта – функции справедливо соотношение:
.
Физически эту функцию можно представлять как бесконечно малый промежуток с суммарным эффектом, равным I.
Дельта-функция обладает следующими “фильтрующими” свойствами для
,
,
.
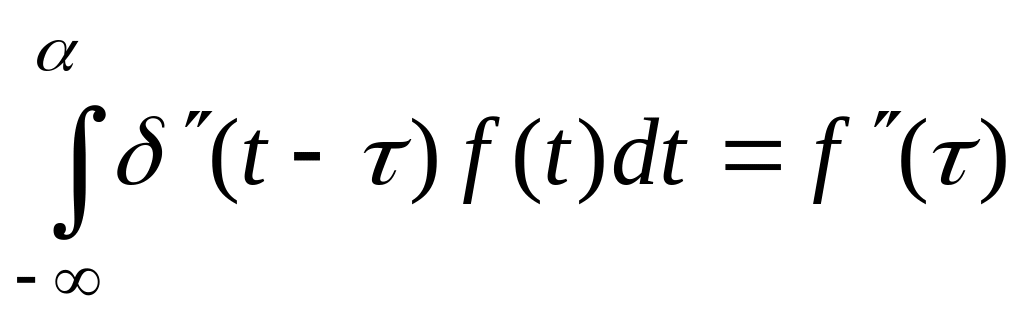Изображение дельта-функции можно
получить предельным переходом при
изображения функции
.
Очевидно
.
По теореме запаздывания получим изображение функции
.
Отсюда
(2.11)
Дельта - функция связана с единичной функцией Хевисайда равенством
.
На дельта функцию распространяются
основные правила операционного
исчисления. Например, по теореме
запаздывания получим
.
Рассмотрим пример, проясняющий
механический смысл
-
функции (дельта - функции).
Пример 1. Решить уравнение
(2.12)
при начальных
условиях
.
Точками обозначены производные по
.
Решение. По теореме о
дифференцировании оригинала имеем
.
Используем формулу (2.11) получаем
Откуда
и по таблице изображений находим решение
поставленной задачи
.
Продифференцируем полученное решение.
Имеем при
.
Поскольку уравнение (2.12) можно рассматривать
как уравнение движения материальной
точки единичной массы, то видно, что
-функция
сообщает такой точке единичную скорость
.
Пусть дано линейное неоднородное
дифференциальное уравнение с постоянными
коэффициентами
(2.13)
Определение. Элементарным
решением дифференциального уравнения
(2.13) называется функция
,
удовлетворяющая уравнению
при нулевых начальных значениях
Известно, что эта функция является также частным решение однородного уравнения
(2.14)
удовлетворяющим условиям
(2.15)
Элементарное решение дифференциального
уравнения обладает важным свойством,
позволяющим находить частное решение
уравнения (2.13), обращающееся в нуль
вместе с производными до
-го
порядка включительно при
:
(2.16)
Следовательно, частное решение уравнения (2.13) вида
удовлетворяет
условиям (2.15). Для получения общего
решения уравнения (2.13) нужно к функции
прибавить общее решение однородного
уравнения (2.14).
Пример 2. Найти решение уравнения
удовлетворяющее условиям
Решение. Найдем элементарное решение уравнения
Выполнив преобразования Лапласа, получим
Используя таблицу изображений, получим
Для отыскания нужного решения найдем
частное решение
:
Искомое частное решение имеет вид
Пример 3. Рассмотрим задачу изгиба прямой балки, принимая гипотезы сопротивления материалов (гипотеза Бернулли плоских сечений).
Пусть прямая балка с осью, направленной
вдоль оси
,
защемлена в точке
и имеет свободный конец в точке
.
Пусть на свободный конец балки действует
сосредоточенная сила
,
направленная в отрицательном направлении
оси
.
Предполагая, что изгиб происходит в
плоскости
найти перемещение балки
.
Решение. Как известно из курса
сопротивления материалов, дифференциальное
уравнение упругой линии балки имеет
вид для
где
-изгибная
жесткость балки,
-нагрузка.
Условия защемления на концах
дают
Из условия для изгибающего момента и перерезывающей силы в точке защемления
Перейдя в уравнении к изображениям, получим
,
.
По таблице изображений
Здесь мы явно ввели функцию Хевисайда, Чтобы подчеркнуть тот факт, что первый член обращается в нуль при . Таким образом, после упрощения получим
