
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко л.П. Цуканова
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко л.П. Цуканова
- •Введение
- •1. Ортогональные системы функций и обобщенные ряды Фурье. Интегралы Фурье
- •1.1. Исторические замечания
- •1.2. Гильбертово пространство. Ряды Фурье в гильбертовом пространстве
- •1.3. Тригонометрические ряды Фурье
- •1.4. Интегральная формула Фурье. Интеграл Фурье
- •1.5. Условия представимости функции интегралом Фурье
- •1.6. Комплексная форма интеграла Фурье. Преобразование Фурье
- •Преобразование Лапласа и его приложения
- •1.1. Свойства преобразования Лапласа
- •2.2. Решение дифференциальных уравнений операционным методом
- •Импульсные функции и их приложение к решению дифференциальных уравнений
- •Приложение операционного метода к решению систем линейных дифференциальных уравнений с постоянными коэффициентами
- •2.5. Индивидуальные задания
- •Ответы к индивидуальным заданиям
- •Задачи механики и физики, приводящие к основным уравнениям математической физики
- •3.1. Понятие уравнения в частных производных и его решения. Основные уравнения математической физики. Уравнения современной математической физики
- •3.2. Уравнения Пуассона и Лапласа. Вывод уравнений для потенциала электрического поля
- •3.3. Получение уравнения Гельмгольца из уравнений электромагнитного поля
- •3.4. Уравнение распространения тепла в изотропном твердом теле
- •3.5. Уравнение колебаний струны
- •4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи Коши
- •4.1. Распространение тепла в неограниченном стержне. Фундаментальное решение уравнения теплопроводности
- •4.2. Метод Фурье для одномерного уравнения теплопроводности. Распространение тепла в ограниченном стержне
- •4.3. Общее решение волнового уравнения в случае одной пространственной переменной. Решение Даламбера
- •4.4. Задача Коши для одномерного волнового уравнения. Формула Даламбера
- •4.5. Колебания ограниченной струны. Решение методом Фурье
- •5. Метод Фурье для уравнений математической физики в двумерном и трехмерном пространствах
- •5.1. Оператор Лапласа в декартовых и криволинейных координатах. Граничные задачи для уравнений Лапласа и Пуассона
- •5.2. Разделение переменных в уравнении Лапласа в декартовой и сферической системах координат
- •5.3. Определение потенциала электрического поля внутри параллелепипеда
- •5.4. Разделение переменных в уравнении Лапласа в цилиндрических координатах
- •5.5. Задача Дирихле для уравнения Лапласа в круге. Интеграл Пуассона
- •5.6. Распространение тепла в бесконечном цилиндре
- •5.7. Распространение электромагнитных волн в цилиндрическом волноводе
- •Решение уравнения Гельмгольца методом Фурье
- •5.8. Движение электрона в атоме водорода. Квантовый подход
- •6. Элементы теории специальных функций
- •6.1. Недостаточность элементарных функций для решений дифференциальных уравнений. Дифференциальные уравнения, как источник функций
- •6.2. Гипергеометрическое уравнение и функции гипергеометрического типа
- •6.3. Частные случаи гипергеометрической функции: цилиндрические функции Бесселя
- •6.4. Частные случаи гипергеометрической функции: ортогональные полиномы Лежандра
- •7. Функциональные и степенные ряды и их приложения к решению дифференциальных уравнений
- •7.1 Функциональные ряды. Сходимость и равномерная сходимость
- •7.2. Свойства равномерно сходящихся рядов. Признак равномерной сходимости
- •7.3. Степенные ряды. Интервал сходимости, радиус сходимости
- •7.4. Свойства степенных рядов
- •7.5. Арифметические операции и другие действия над степенными рядами
- •7.6. Разложение функций в степенные ряды
- •7.7. Обобщения степенных рядов – интегро – степенные ряды и ряды Вольтерра
- •8. Приближенно-аналитические методы решения дифференциальных уравнений
- •8.1. Необходимость асимптотических методов
- •8.2. Калибровочные функции. Символы порядка
- •8.3. Пример асимптотического разложения. Определение асимптотического ряда
- •8.4. Асимптотические последовательности и асимптотические разложения
- •8.5. Простейшие асимптотические методы решения дифференциальных уравнений
- •8.6. Метод Линдстедта – Пуанкаре
- •1. Ортогональные системы функций .И обобщенные ряды Фурье. Интегралы Фурье……………………………………..... 4
- •2. Преобразование Лапласа и его приложения…………….19
- •2.3. Импульсные функции и их приложение к решению дифференциальных уравнений …………….……….……..…... 38
- •3. Задачи механики и физики, приводящие к основным уравнениям математической физики ……………………......76
- •4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи ……...……………107
- •5. Метод Фурье для уравнений математической физики в двумерном и трехмерном пространствах .......…………….133
- •6. Элементы теории специальных функций.........................179
- •8. Приближенно-аналитические методы решения дифференциальных уравнений ….........................................221
- •9. Список литературы………………………………………..247
- •394026 Воронеж, Московский просп., 14
7.4. Свойства степенных рядов
Члены степенного ряда, т.е. функции
![]() являются непрерывными и даже непрерывно
дифференцируемыми функциями при любых
значениях
.
Поэтому из теоремы о равномерной
сходимости степенного ряда вытекают
следующие его свойства.
являются непрерывными и даже непрерывно
дифференцируемыми функциями при любых
значениях
.
Поэтому из теоремы о равномерной
сходимости степенного ряда вытекают
следующие его свойства.
Сумма степенного ряда
 (7.7)
(7.7)
непрерывна в каждой внутренней точке интервала сходимости (здесь и далее предполагается, что интервал сходимости не вырождается в точку ). Если ряд (7.7) сходится в каком – либо из концов интервала сходимости , то его сумма будет непрерывной и в этом конце.
2. Степенной ряд (7.7) можно почленно дифференцировать во внутренних точках интервала сходимости, т.е. в них его сумма дифференцируема и выполняется равенство
 (7.8)
(7.8)
причем производный ряд (7.8) имеет тот же интервал сходимости, что и ряд (7.7).
3. Из предыдущего свойства вытекает: сумма степенного ряда (7.7) имеем производные всех порядков, причем

![]() .
(7.9)
.
(7.9)
4. Степенной ряд (7.7) можно интегрировать почленно в интервале сходимости
 (7.10)
(7.10)
причем радиусы сходимости (7.10) и (7.7) совпадает.
Пример. Используя свойства степенных рядов, найти сумму ряда

![]()
Решение. Обозначим сумму ряда через и применим утверждение, выраженное свойством 2. Получаем
 при
при
Отсюда имеем

Пример. Применяя почленное интегрирование вычислить сумму ряда
![]()
Решение. Обозначая искомую сумму ряда через , имеем
![]()

Интегрируя почленно, получим

где

Таким образом,
![]() .
Далее интегрируем почленно ряд для
.
Далее интегрируем почленно ряд для
![]()
 .
.
Последний ряд представляет собой
геометрическую прогрессию со знаменателем
![]() .
Таким образом, имеем
.
Таким образом, имеем


Следовательно,
![]()
7.5. Арифметические операции и другие действия над степенными рядами
В данном пункте помещен справочный материал, который не входит в обязательную программу изучения степенных рядов в техническом вузе. Однако для аспирантов и инженеров – исследователей приведенные здесь формулы могут оказаться весьма полезными. Некоторые из этих формул либо вообще отсутствуют в учебной литературе, либо приведены в непригодной для использования форме. Мы приводим также обобщения некоторых известных формул
1. Сложение, вычитание и умножение степенных рядов.
Пусть два степенных ряда


сходятся
к суммам
![]() ,
,
![]() и
и
![]() - радиусы сходимости этих рядов. Тогда
сходятся ряды
- радиусы сходимости этих рядов. Тогда
сходятся ряды


где
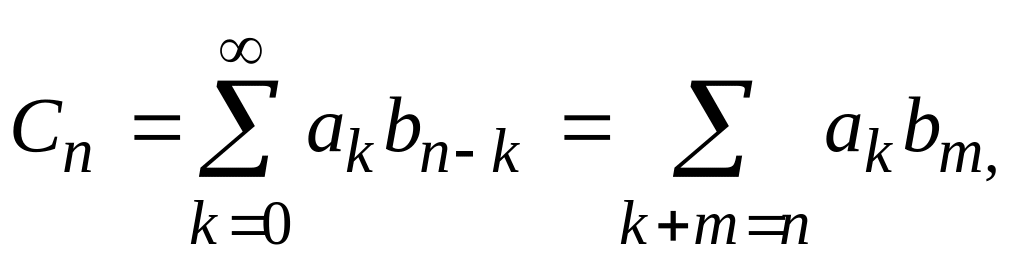 (7.11)
(7.11)
при
![]() .
Последняя сумма в выражении для
коэффициента
.
Последняя сумма в выражении для
коэффициента
![]() берется по возможным целым неотрицательным
решениям уравнения
берется по возможным целым неотрицательным
решениям уравнения
![]() при заданном индексе
.
при заданном индексе
.
В случае произведения
![]() рядов можно получить по индукции
выражение
рядов можно получить по индукции
выражение
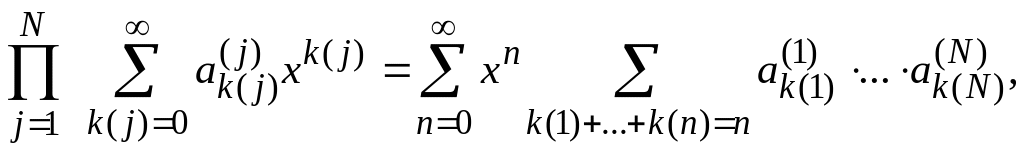 (7.12)
(7.12)
где
внутренняя сумма в правой части берется
по целым неотрицательным решениям
уравнения
![]() ,
а радиус сходимости ряда в правой части
равенства
,
а радиус сходимости ряда в правой части
равенства
![]() .Сумма
же ряда, равного произведению
рядов, будет равна произведению сумм:
.Сумма
же ряда, равного произведению
рядов, будет равна произведению сумм:

2. Деление степенных рядов.
Если
,
и
![]() ,
то при достаточно малых значениях
,
то при достаточно малых значениях
![]() справедливо следующее разложение в
степенной ряд частного:
справедливо следующее разложение в
степенной ряд частного:
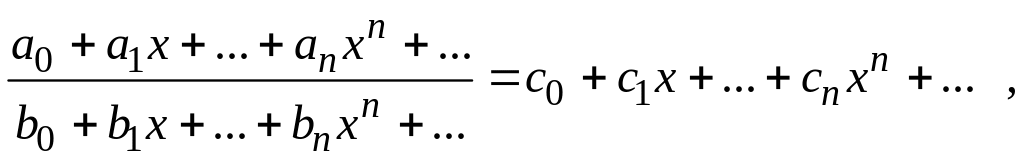
коэффициенты
![]() которого можно найти по рекуррентным
формулам, полученным в результате
умножения степенных рядов
которого можно найти по рекуррентным
формулам, полученным в результате
умножения степенных рядов

Используя формулы (7.10) и приравняв коэффициенты при одинаковых степенях в правой и левой частях равенства, получим

![]() (7.13)
(7.13)

Из формул (7.13) видно, что коэффициенты
![]() последовательно находятся из цепочки
уравнений при условии
.
последовательно находятся из цепочки
уравнений при условии
.
3. Обратный элемент для сходящегося степенного ряда.
На основе приведенных результатов по
делению степенных рядов можно ввести
обратный ряд для ряда
 .
По определению, ряд
.
По определению, ряд
 называется обратным для ряда
называется обратным для ряда
![]() ,
если
,
если
![]()
Справедливо
утверждение: если радиус сходимости
ряда
отличен от нуля, то обратный ряд
![]() имеет не равный нулю радиус сходимости.
имеет не равный нулю радиус сходимости.
Из формул (7.13) как частный случай
получаются уравнения для определения
коэффициентов
![]() ряда
.
Выполняя умножение, имеем
ряда
.
Выполняя умножение, имеем
 .
.
Отсюда, используя формулы (7.13), получаем
![]()
 (7.14)
(7.14)
где
символ Кронекера
![]() при
при
![]() ,
,
![]() при
при
![]() .
Из рекуррентной системы (7.14) последовательно
находятся коэффициенты ряда
:
.
Из рекуррентной системы (7.14) последовательно
находятся коэффициенты ряда
:
![]()
4. Подстановка ряда в ряд.
Пусть функция
![]() в промежутке
является суммой степенного ряда
в промежутке
является суммой степенного ряда
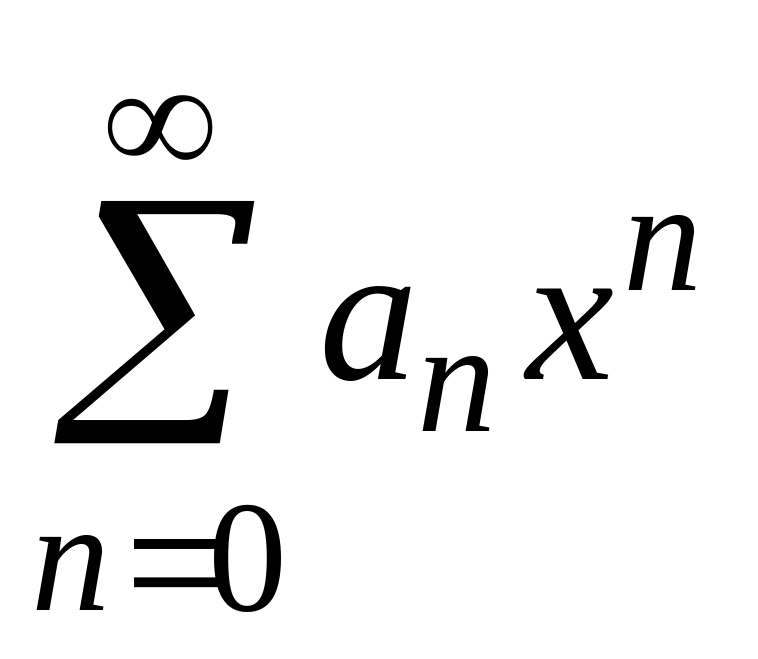 ,
а функция
,
а функция
![]() является суммой степенного ряда в
промежутке
является суммой степенного ряда в
промежутке
![]()
 (7.15)
(7.15)
Справедливо утверждение: при условии
![]() ,
сложная функция
,
сложная функция
![]() в окрестности точки
является суммой степенного ряда,
полученного подстановкой в (7.15) вместо
ряда
,
возведения в соответствующие степени
и объединения затем подобных членов.
в окрестности точки
является суммой степенного ряда,
полученного подстановкой в (7.15) вместо
ряда
,
возведения в соответствующие степени
и объединения затем подобных членов.
Используя частный случай формулы
(7.12) при
![]() ,
получим выражения для композиции рядов
и
,
получим выражения для композиции рядов
и
 ,
(7.16)
,
(7.16)
где
последняя сумма в правой части равенства
(7.16) берется по целым неотрицательным
решениям уравнения
![]() .
.
В развернутом виде формула (7.16) выглядит так
![]()
![]()
![]() .
.
5. Обращение степенного ряда.
Пусть необходимо найти из уравнения , где функция задана в виде степенного ряда

![]() .
(7.17)
.
(7.17)
Обратную функцию для функции
обозначим
![]() .
Поскольку функция
задана не в замкнутом виде, а в виде
ряда, то и обратную функцию возможно
построить лишь в виде ряда
.
Поскольку функция
задана не в замкнутом виде, а в виде
ряда, то и обратную функцию возможно
построить лишь в виде ряда
 .
(7.18)
.
(7.18)
Так мы приходим к задаче об обращении степенных рядов.
Справедливо утверждение. Пусть
степенной ряд, такой, что
![]() ,
,
![]() .
- ряд обратный ряду
относительно композиции, т.е. степенной
ряд, такой, что
.
- ряд обратный ряду
относительно композиции, т.е. степенной
ряд, такой, что
![]() и
и
![]() .
Если радиус сходимости
отличен от нуля, то это же справедливо
для ряда
.
.
Если радиус сходимости
отличен от нуля, то это же справедливо
для ряда
.
Получим соотношение, связывающие искомые
коэффициенты
![]() с заданными величинами
с заданными величинами
![]() .
Подставим
из (7.18) в ряд (7.17) и воспользуемся (7.16).
Получим
.
Подставим
из (7.18) в ряд (7.17) и воспользуемся (7.16).
Получим

Изменив порядок суммирования в двух первых суммах, запишем окончательно
 .
(7.19)
.
(7.19)
Приравнивая в (7.19) коэффициенты при одинаковых степенях в правой и левой частях равенства, получим рекуррентную систему уравнений, определяющую коэффициенты ряда (7.18):
![]() (7.20)
(7.20)
![]()
![]()
…………………………………………………………………
![]() .
.
Отсюда последовательно находятся коэффициенты :
![]()
Пример. Зная разложение в ряд
функции
![]() ,
найти разложение в ряд функции
,
найти разложение в ряд функции
![]() .
.
Решение. Считаем известным разложение в степенной ряд функции
![]() .
.
Ищем разложение обратной функции в виде
![]()
Записанный ряд содержит только нечетные степени , т.к. функция нечетная и потому обратная к ней функция также нечетная.
Из формулы (7.19) имеем:
![]()
![]()
![]()
Получаем
![]() .
.
