6.3. Частные случаи гипергеометрической функции: цилиндрические функции Бесселя

Выполнив в гипергеометрическом уравнении (6.2) замену переменной разделив обе части полученного уравнения на и переходя к пределам и получим дифференциальное уравнение

.

Введя новую функцию , где постоянная выбрана через , а новую независимую переменную снова через , получаем дифференциальное уравнение Бесселя (см. [12], п.5)

. (6.6)

Его линейно независимое решение (для не целых ) называются цилиндрическими функциями Бесселя первого рода и

(6.7)

Эти функции, как известно из теории специальных функций [13], следующим образом выражаются через гипергеометрическую функцию (6.3)

Общее решение уравнения (6.6) при неравном целому числу, имеет вид

Известны также представления функции Бесселя через вырожденную гипергеометрическую функцию (6.4)

Выражения функции Бесселя через некоторые элементарные функции (при частных значениях индекса ) приведены в [11].

При где - натуральное число, функция Бесселя представляется рядом

(6.8)

причем

Следовательно, при целом функции и линейно зависимы.

Приведем для справок ряды для часто встречающихся функций Бесселя:

Для целых значений индекса линейно независимым от решением уравнения Бесселя является функция Вебера где называется бесселевой функцией второго рода порядка Представление функции степенным рядом приведено в методических указаниях [11] или в справочнике [12].

Задачи для самостоятельного решения к п.6.3.

1. Используя ряды для цилиндрических функций первого рода (6.7) и степенные ряды для элементарных функций, показать справедливость равенств

1)

2)

2. Основываясь на вырожденном гипергеометрическом ряде (6.4) и рядах для функций Бесселя (6.7), показать

1)

2)

3)

где - модифицированная бесселевая функция первого рода порядка

6.4. Частные случаи гипергеометрической функции: ортогональные полиномы Лежандра

Дифференциальное уравнение Гаусса (6.2) в важных для приложений частных случаях имеет решения в виде ортогональных полиномов. Покажем, что уравнение (6.2) может иметь решение в виде полинома степени . Для этого в выражении (6.3) для функции Гаусса положим , где - целое число.

Общий член гипергеометрического ряда (6.3) содержит множители включающие , которые при принимают вид

При это выражение обращается в ноль. Поэтому ряд Гаусса превращается в полином степени

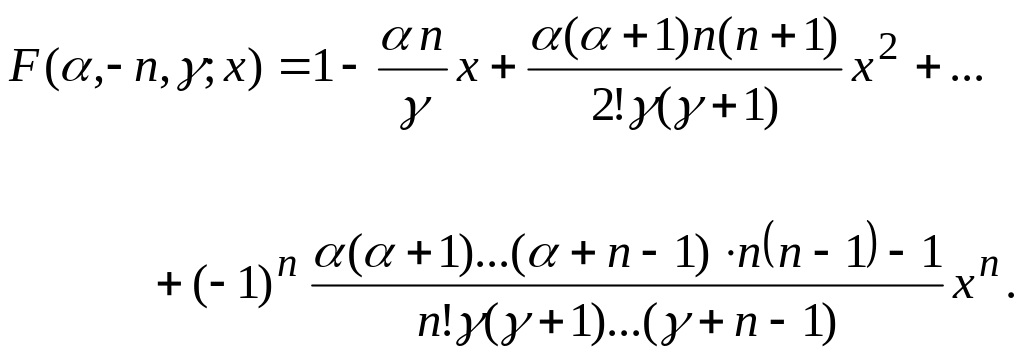(6.9)

Таким образом, если в гипергеометрическом дифференциальном уравнении (6.2) положить где целое положительное число, то в числе его решений будут многочлены степени .

Замечание: В п.6.2 мы рассматривали лишь одно частное решение дифференциального уравнения второго порядка (6.2) в виде гипергеометрической функции. Другое частное решение мы не рассматривали.

Выбирая в гипергеометрическом уравнении параметры и определенным образом можно получить при решения в виде различного рода полиномов. Однако наибольший интерес для приложений имеют ортогональные полиномы.

Выберем в уравнении Гаусса (6.2) , , . Тогда уравнение (6.2) примет вид

. (6.10)

Введем новую независимую переменную . Тогда , ,

, .

Заменив теперь букву снова на букву получим дифференциальное уравнение (6.10) в виде

, (6.11)

или

. (6.12)

Дифференциальное уравнение (6.11) или (6.12) называется уравнением Лежандра.

Одним из частных решений уравнения Лежандра является полином Лежандра

. (6.13)

Это выражение можно получить непосредственно, решая уравнение (6.14) в степенных рядах [11] или из гипергеометрического ряда (6.3), учитывая равенство

. (6.14)

В необходимом объеме этот материал изложен в методических указаниях [11] книге [13].

Упражнение. Получить выражение (6.13) для полинома Лежандра из гипергеометрического ряда (6.3) используя представление (6.14).

Полиномы Лежандра наиболее экономным способом можно получить из формулы Родрига полученной им в 1815 году

(6.15)

или исходя из производящей функции

в соответствии с соотношением

. (6.16)

Для нескольких первых номеров полиномы Лежандра имеют вид

(6.17)

.

В методических указаниях [11] приводится построение решения уравнения Лежандра (6.11) для и , а также выражения для при .

Задачи для самостоятельного решения к п.6.4.

1. Используя формулу Родрига (6.15) получить выражения для , , .

2. Используя производящую формулу (6.16) получить многочлен Лежандра , и .

3. Исходя из значения производящей функции для , показать справедливость формул: