
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко л.П. Цуканова
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко л.П. Цуканова
- •Введение
- •1. Ортогональные системы функций и обобщенные ряды Фурье. Интегралы Фурье
- •1.1. Исторические замечания
- •1.2. Гильбертово пространство. Ряды Фурье в гильбертовом пространстве
- •1.3. Тригонометрические ряды Фурье
- •1.4. Интегральная формула Фурье. Интеграл Фурье
- •1.5. Условия представимости функции интегралом Фурье
- •1.6. Комплексная форма интеграла Фурье. Преобразование Фурье
- •Преобразование Лапласа и его приложения
- •1.1. Свойства преобразования Лапласа
- •2.2. Решение дифференциальных уравнений операционным методом
- •Импульсные функции и их приложение к решению дифференциальных уравнений
- •Приложение операционного метода к решению систем линейных дифференциальных уравнений с постоянными коэффициентами
- •2.5. Индивидуальные задания
- •Ответы к индивидуальным заданиям
- •Задачи механики и физики, приводящие к основным уравнениям математической физики
- •3.1. Понятие уравнения в частных производных и его решения. Основные уравнения математической физики. Уравнения современной математической физики
- •3.2. Уравнения Пуассона и Лапласа. Вывод уравнений для потенциала электрического поля
- •3.3. Получение уравнения Гельмгольца из уравнений электромагнитного поля
- •3.4. Уравнение распространения тепла в изотропном твердом теле
- •3.5. Уравнение колебаний струны
- •4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи Коши
- •4.1. Распространение тепла в неограниченном стержне. Фундаментальное решение уравнения теплопроводности
- •4.2. Метод Фурье для одномерного уравнения теплопроводности. Распространение тепла в ограниченном стержне
- •4.3. Общее решение волнового уравнения в случае одной пространственной переменной. Решение Даламбера
- •4.4. Задача Коши для одномерного волнового уравнения. Формула Даламбера
- •4.5. Колебания ограниченной струны. Решение методом Фурье
- •5. Метод Фурье для уравнений математической физики в двумерном и трехмерном пространствах
- •5.1. Оператор Лапласа в декартовых и криволинейных координатах. Граничные задачи для уравнений Лапласа и Пуассона
- •5.2. Разделение переменных в уравнении Лапласа в декартовой и сферической системах координат
- •5.3. Определение потенциала электрического поля внутри параллелепипеда
- •5.4. Разделение переменных в уравнении Лапласа в цилиндрических координатах
- •5.5. Задача Дирихле для уравнения Лапласа в круге. Интеграл Пуассона
- •5.6. Распространение тепла в бесконечном цилиндре
- •5.7. Распространение электромагнитных волн в цилиндрическом волноводе
- •Решение уравнения Гельмгольца методом Фурье
- •5.8. Движение электрона в атоме водорода. Квантовый подход
- •6. Элементы теории специальных функций
- •6.1. Недостаточность элементарных функций для решений дифференциальных уравнений. Дифференциальные уравнения, как источник функций
- •6.2. Гипергеометрическое уравнение и функции гипергеометрического типа
- •6.3. Частные случаи гипергеометрической функции: цилиндрические функции Бесселя
- •6.4. Частные случаи гипергеометрической функции: ортогональные полиномы Лежандра
- •7. Функциональные и степенные ряды и их приложения к решению дифференциальных уравнений
- •7.1 Функциональные ряды. Сходимость и равномерная сходимость
- •7.2. Свойства равномерно сходящихся рядов. Признак равномерной сходимости
- •7.3. Степенные ряды. Интервал сходимости, радиус сходимости
- •7.4. Свойства степенных рядов
- •7.5. Арифметические операции и другие действия над степенными рядами
- •7.6. Разложение функций в степенные ряды
- •7.7. Обобщения степенных рядов – интегро – степенные ряды и ряды Вольтерра
- •8. Приближенно-аналитические методы решения дифференциальных уравнений
- •8.1. Необходимость асимптотических методов
- •8.2. Калибровочные функции. Символы порядка
- •8.3. Пример асимптотического разложения. Определение асимптотического ряда
- •8.4. Асимптотические последовательности и асимптотические разложения
- •8.5. Простейшие асимптотические методы решения дифференциальных уравнений
- •8.6. Метод Линдстедта – Пуанкаре
- •1. Ортогональные системы функций .И обобщенные ряды Фурье. Интегралы Фурье……………………………………..... 4
- •2. Преобразование Лапласа и его приложения…………….19
- •2.3. Импульсные функции и их приложение к решению дифференциальных уравнений …………….……….……..…... 38
- •3. Задачи механики и физики, приводящие к основным уравнениям математической физики ……………………......76
- •4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи ……...……………107
- •5. Метод Фурье для уравнений математической физики в двумерном и трехмерном пространствах .......…………….133
- •6. Элементы теории специальных функций.........................179
- •8. Приближенно-аналитические методы решения дифференциальных уравнений ….........................................221
- •9. Список литературы………………………………………..247
- •394026 Воронеж, Московский просп., 14
7.2. Свойства равномерно сходящихся рядов. Признак равномерной сходимости
В отличии от рядов, сходящихся поточечно,
равномерно сходящиеся ряды обладают
свойством коммутативности суммирования
и предельного перехода:
![]() .
Таким образом, коллективное свойство
членов ряда – равномерная сходимость,
приводит к качественно новым свойствам
его суммы.
.
Таким образом, коллективное свойство
членов ряда – равномерная сходимость,
приводит к качественно новым свойствам
его суммы.
Наиболее важными свойствами равномерно сходящихся рядов являются следующие.
Сумма конечного числа равномерно сходящихся рядов является равномерно сходящимся рядом.
Умножение всех членов равномерно сходящегося ряда на одну и ту же ограниченную функцию
 (в частности, на постоянную) не нарушает
равномерной сходимости.
(в частности, на постоянную) не нарушает
равномерной сходимости.Если все члены функционального ряда непрерывны на
 и ряд сходится равномерно на
,
то его сумма также непрерывна на
.
и ряд сходится равномерно на
,
то его сумма также непрерывна на
.Если функциональный ряд, члены которого непрерывны на сходится равномерно на этом отрезке и
 - его сумма, то имеет место равенство
- его сумма, то имеет место равенство
 при любых
и
при любых
и
![]() из
из
![]()
5. Если функциональный ряд сходится на
,
его члены являются непрерывно
дифференцируемыми на
,
а ряд производных
![]() сходится равномерно на
,
то сумма ряда
дифференцируема на
и справедливо равенство
сходится равномерно на
,
то сумма ряда
дифференцируема на
и справедливо равенство
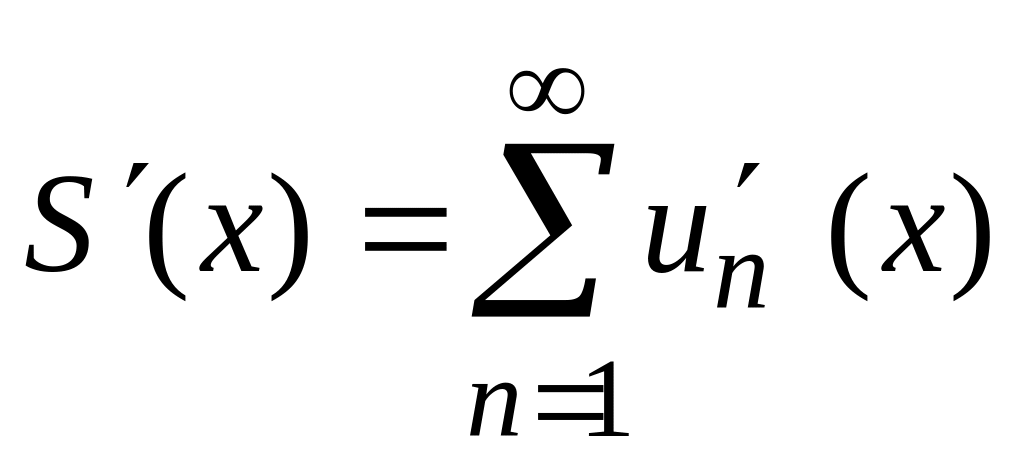 .
.
Для установления на практике равномерной сходимости конкретных рядов затруднительно использовать определение равномерной сходимости. С этой целью пользуются более удобными в применении достаточными признаками.
Мажорантный признак
Вейерштрасса. Если члены
функционального ряда (7.1) удовлетворяют
на
неравенствам
![]() ,
,
![]() ,
где
,
где
![]() - члены сходящегося числового ряда,
(называемого мажорирующим рядом),
то ряд (7.1) сходится равномерно на
.
- члены сходящегося числового ряда,
(называемого мажорирующим рядом),
то ряд (7.1) сходится равномерно на
.
Пример. Рассмотрим ряд
 при
при
![]() .
.
Ряд
сходится равномерно на всей оси, так
как для него существует мажорирующий
сходящийся числовой ряд
![]() ,
поскольку справедливо неравенство
,
поскольку справедливо неравенство
![]() .
.
Пример. Дан ряд
 .
Известна его сумма
.
Известна его сумма
![]() Показать, что данный ряд можно
дифференцировать почленно и найти сумму
ряда
Показать, что данный ряд можно
дифференцировать почленно и найти сумму
ряда
![]() ,
составленного из производных исходного
ряда.
,
составленного из производных исходного
ряда.
Решение. Вычислим производную
общего члена ряда:
![]() .
Полученный ряд
.
Полученный ряд
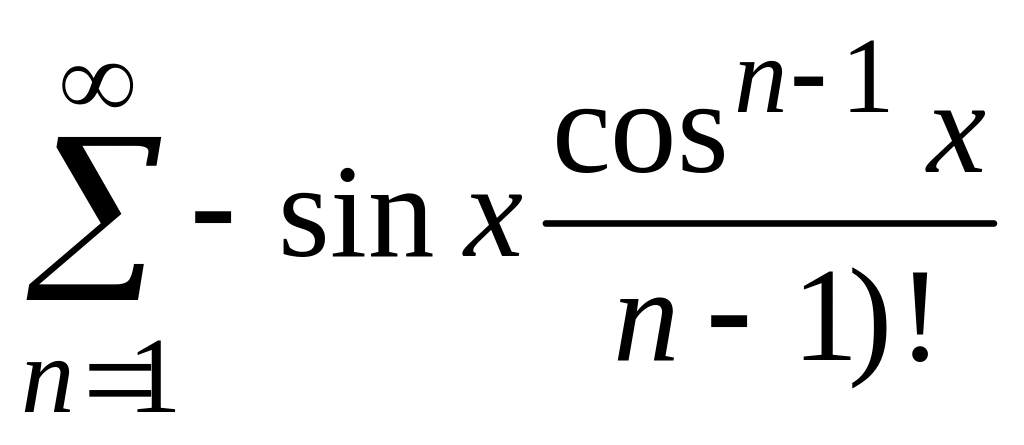 сходится равномерно, так как справедлива
оценка
сходится равномерно, так как справедлива
оценка
 ,
а мажорирующий числовой ряд
,
а мажорирующий числовой ряд
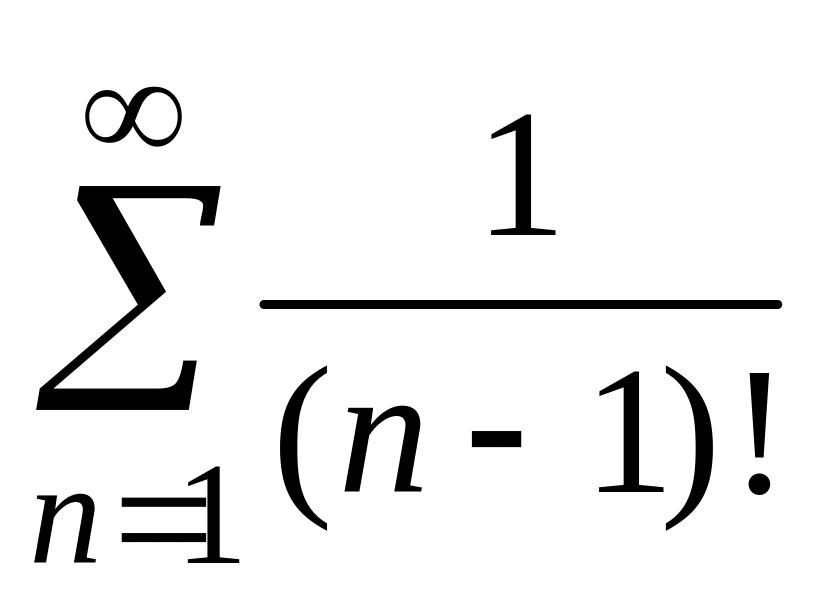 сходится. Поэтому
сходится. Поэтому
![]()
7.3. Степенные ряды. Интервал сходимости, радиус сходимости
Степенным рядом называется функциональный ряд вида
 (7.4)
(7.4)
где
коэффициенты
![]() - постоянные числа.
- постоянные числа.
Если сделать замену
![]() на
,
то степенной ряд примет вид
на
,
то степенной ряд примет вид
 .
(7.5)
.
(7.5)
Поэтому в дальнейшем ограничимся рассмотрением рядов вида (7.5).
В отличии от области сходимости
произвольного функционального ряда,
которая может оказаться множеством
сколь угодно сложной структуры, область
сходимости ряда (7.5) всегда является
отрезком оси
![]() ,
который может быть сегментом, полусегментом
или интервалом, может вырождаться в
одну точку
,
который может быть сегментом, полусегментом
или интервалом, может вырождаться в
одну точку
![]() или совпадать со всей осью
.
Очевидно, что всякий степенной ряд вида
(7.5) сходится при
.Существуют
степенные ряды, сходящиеся только
в точке
.
или совпадать со всей осью
.
Очевидно, что всякий степенной ряд вида
(7.5) сходится при
.Существуют
степенные ряды, сходящиеся только
в точке
.
Пример. Ряд вида
 сходится при
и расходится при любом
сходится при
и расходится при любом
![]() .
Действительно, при
по признаку Даламбера имеем
.
Действительно, при
по признаку Даламбера имеем

Следовательно, при ряд расходится. С другой стороны, степенной ряд для показательной функции
![]()
сходится при всех , т.е. его область сходимости – вся ось. Этот факт легко проверить, применяя признак Даламбера, как в предыдущем примере. Характер сходимости степенного ряда описывается следующей основной теоремой.
Теорема Абеля. Если
степенной ряд (7.5) сходится при некотором
значении
![]() ,
то он сходится, и притом абсолютно, при
всех значениях
,
для которых
,
то он сходится, и притом абсолютно, при
всех значениях
,
для которых
![]() .
Сходимость ряда будет равномерной во
всяком интервале
.
Сходимость ряда будет равномерной во
всяком интервале
![]() ,
где
,
где
![]() - любое положительное число, меньше, чем
- любое положительное число, меньше, чем
![]() .
.
Если степенной ряд расходится в точке
,
то он расходится и во всех точках
таких, что
![]() .
.
Из этой теоремы вытекает, что если
область сходимости степенного ряда не
вырождается в точку
и не совпадает со всей осью, то существует
число
такое, что при
![]() ряд сходится, а при
ряд сходится, а при
![]() - расходится.
- расходится.
Число
называется радиусом сходимости
степенного ряда, интервал
![]() называется интервалом сходимости
степенного ряда.
называется интервалом сходимости
степенного ряда.
Для вычисления радиуса сходимости степенного ряда вида (7.5) используется одна из следующих формул:

 (7.6)
(7.6)
Для нахождения области сходимости
степенного ряда нужно найти радиус его
сходимости и затем проверить сходимость
ряда при
![]() .
.
Пример. Найти область сходимости
ряда

Решение. Воспользуемся первой из формул (7.6), имеем

Это
означает, что ряд сходится при всех
значениях
из
![]() .
.
Пример. Найти область сходимости
ряда
![]() .
.
Решение. Найдем радиус сходимости ряда по формуле (6.6)
![]()
Следовательно, интервалом сходимости
ряда является
(-1,1). Определим, сходится
ли ряд на концах интервала. При
имеем гармонический ряд
![]() ,
который, как известно, расходится. При
,
который, как известно, расходится. При
![]() получаем знакочередующийся ряд
получаем знакочередующийся ряд
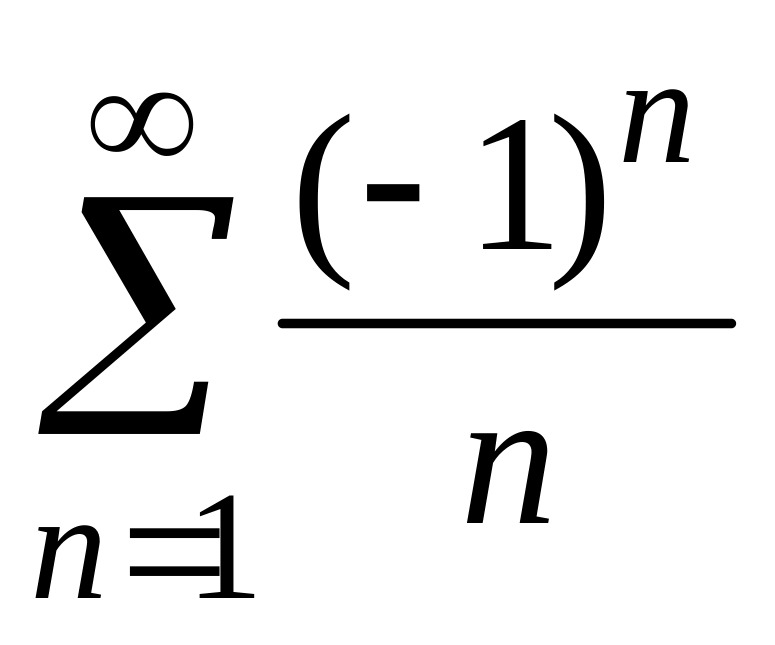 .
Применим признак Лейбница о сходимости
знакочередующихся рядов.
.
Применим признак Лейбница о сходимости
знакочередующихся рядов.
Вычислим
![]()
Проверим условие монотонного убывания членов ряда:
![]() .
.
Таким образом, ряд сходится при
Область его сходимости
![]() .
.
