3.5. Уравнение колебаний струны

Рассмотрим натянутую струну, закрепленную на концах и . Под струной понимают тонкую нить, которая может свободно изгибаться, т.е. не оказывает сопротивление изменению ее формы, не связанному с изменением ее длины. Сила натяжения , действующая на струну, предполагается значительной, так что действием силы тяжести можно пренебречь.

Пусть в положении равновесия струна направлена по оси . В момент времени струна выводится из положения равновесия. Будем рассматривать только поперечное колебание струны, предполагая что движение точек струны происходит в плоскости , где - смещение точек струны в момент времени от положения равновесия. При фиксированном график функции дает форму струны в этот момент времени.

Ограничимся рассмотрением лишь малых колебаний струны, при которых смещение и производная столь малы, что их квадратами и произведениями можно пренебречь по сравнению с самими этими величинами.

0

Рис. 5

Выделим произвольный участок струны (рис.5), который при колебании деформируется в участок длина которого равна . Как известно из математического анализа, для дифференциала дуги справедливо выражение

.

Пренебрегая величиной получим . Это означает, что в процессе малых колебаний удлинение участков струны не происходит (с точностью до малых более высокого порядка малости, чем и ). По закону Гука действующая сила пропорциональна изменению длины элемента. Но поскольку мы пренебрегаем изменениями длины, то натяжение струны по величине не меняется со временем. Таким образом, при сделанных предположениях изменением величины натяжения струны, возникающим при ее движении, можно пренебречь по сравнению с натяжением, которому струна была подвергнута в положении равновесия.

Покажем, что величину натяжения можно считать независящей от , т.е. . Действительно, на участок струны действуют силы натяжения, направленные по касательным в точках и , внешние силы и силы инерции. Сумма проекций всех сил на ось должна быть равна нулю. Силы инерции и внешние силы перпендикулярны оси , т.к. рассматриваются только поперечные колебания. Баланс проекций сил натяжения

(3.38)

где - угол между касательной в точке с абсциссой в момент времени с положительным направлением оси . Учитывая, что , имеем

где пренебрегли величиной . Заменяя на получим также единицу. Таким образом, из (3.38) вытекает, что . Ввиду произвольности можно считать величину натяжения постоянной и для всех значений и .

Для получения уравнения колебаний струны воспользуемся принципом Даламбера – все силы, действующие на выделенный участок в струне, включая силы инерции, должны уравновешиваться.

Рассмотрим снова произвольный участок струны и составим условие равенства нулю суммы проекций сил на ось : сил натяжения, равных по величине и направленных по касательным к струне в точках и , внешней силы, направленной параллельно оси , и силы инерции.

Сумма проекций на ось сил натяжения, действующих в точках и

Поскольку

то имеем

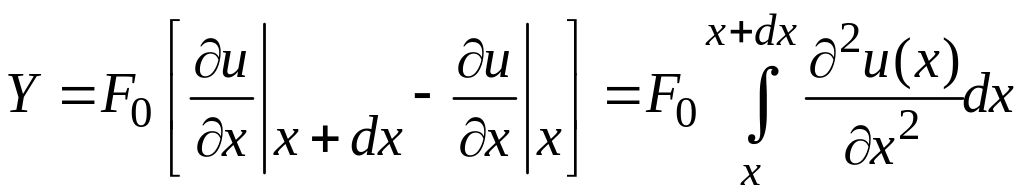. (3.39)

Обозначим внешнюю силу, действующих на струну параллельно оси и отнесенную к единице длины струны. Проекция этой силы на ось , действующей на участок , будет равна

(3.40)

Пусть - линейная плотность струны. Тогда сила инерции дуги будет равна

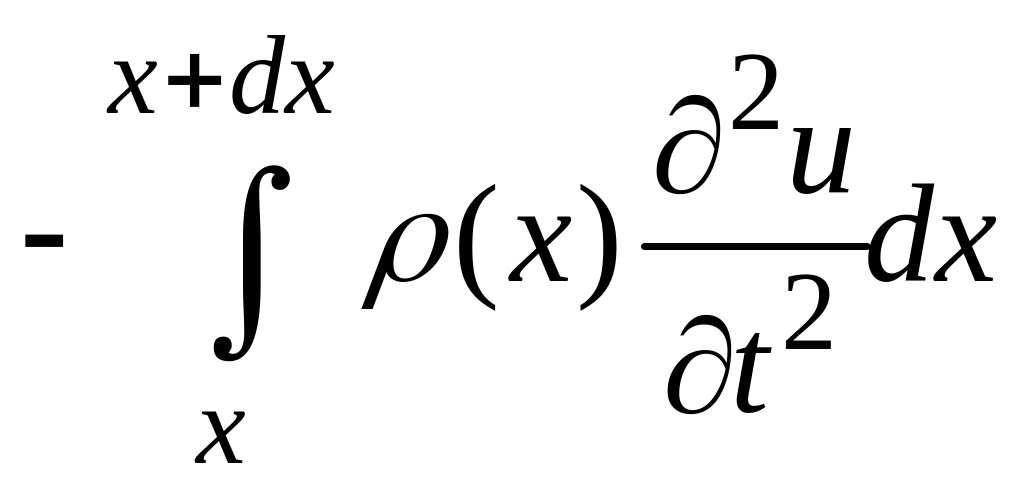(3.41)

Суммируя проекции (3.39) - (3.41) на ось всех сил, действующих на , приравнивая эту сумму нулю, получаем

.

Ввиду произвольности и заключаем, что подынтегральная функция должна быть равна нулю для каждой точки в любой момент

. (3.42)

Это уравнение называется дифференциальным уравнением колебаний струны.

Для однородной струны . Обозначив получим

. (3.43)

Если внешняя сила отсутствует, то и получаем уравнение свободных колебаний струны

. (3.44)

Уравнение (3.44) часто называют волновым уравнением, а уравнение (3.43) – неоднородным волновым уравнением. С изложенным материалом можно ознакомиться также по учебнику [1], гл. 18.

Уравнения (3.42) – (3.44) имеют бесчисленное множество частных решений. Поэтому только одного уравнения недостаточно для полного определения движения струна. Нужны дополнительные условия, вытекающие из физического содержания задачи. Именно, в начальный момент времени нужно задать начальные условия – положение и скорость всех точек струны

(3.45)

Поскольку струна ограничена, нужно указать, что происходит на ее концах. Для закрепленной струны на концах должны выполняться условия

при (3.46)

Эти условия называются краевыми или граничными условиями. Возможны, конечно, и другие краевые условия.

Если рассматриваются поперечные колебания тонкой пластинки, закрепленной по ее контуру, так, что каждая точка движется перпендикулярно плоскости , параллельно оси , то смещение точек пластинки будут удовлетворять двумерному волновому уравнению

(3.47)

Начальные условия в этом случае имеют вид

Краевое условие для закрепленной по контуру пластинки должно быть следующего вида

где - контур закрепления.

При колебаниях объемных тел уравнение движения точек среды имеет вид трехмерного волнового уравнения для

Физический пример: волны в 2-х проводной линии

Всякую линию передачи можно упрощенно представить в виде двух параллельных проводов, к концу которой присоединен генератор переменного тока. На рис. 6 показана линия в тот момент, когда вывод А генератора положителен относительно вывода В и создаваемый генератором ток течет от вывода к выводу В. Через половину периода положение меняется на обратное. В результате вдоль каждого провода устанавливается распределение зарядов, меняющее знак через каждую половину периода соответственно гармоническим колебаниям электрического заряда.

Пусть производится наблюдение тока и напряжения в двух соседних точках идеальной (без потерь) передающей линии, находящихся на расстояниях и от начала линии (рис. 7).

+ + - - - + +

А + + + - - + + +

гене-ратор

V_max

Поток

энергии

V_max

+ + + + +

B _ _ _ _ _ _

_ _ _ _

Бесконечно длинная линия передачи

Рис. 6

Провод 1 I(x) I(x+ x)

V(x) V(x+ x)

Провод 2 x x+ x

Токи и напряжения в передающей линии

Рис. 7

Провода передающей линии образуют конденсатор, погонную емкость которого обозначим . Токи, существующие в линии, создают магнитный поток, пронизывающий область между проводами. Поэтому линия характеризуется также погонной индуктивностью . Эквивалентная схема участка двухпроводной линии показана на рис.8.

L₀

I+ x

∩∩∩∩

I

V+ x

C₀

Схема элемента идеальной линии передачи

Рис. 8

Если ток в линии меняется, то индуктивность вызовет падение напряжения вдоль участка линии от до

где - индуктивность элемента длины линии. Разделив обе части равенства на и переходя к пределу при →0, получаем

(3.48)

Таким образом, изменение тока во времени приводит к перепаду напряжения. Если напряжение в точке меняется (см. рис. 7), то должны появиться заряды, которые на этом участке передаются емкости. На участке от до , появляющийся при этом заряд, равен где – емкость на единицу длины.

Скорость изменения этого заряда равна . Но заряд может изменяться на участке только тогда, когда входящий в элемент ток не равен выходящему току . Пусть ∆I разность этих токов, тогда имеем

Разделив равенство на и переходя к пределу при →0, получим

. (3.49)

Последнее означает, что сохранение заряда предполагает, что градиент тока пропорционален скорости изменения напряжения во времени.

Уравнения (3.48) и (3.49) – это основные уравнения линии передачи для простейшей идеализации, не учитывающей сопротивление проводников и возможную утечку зарядов через изоляцию между проводниками.

Из уравнений (3.48) и (3.49) можно получить дифференциальное уравнение для одной из функций или , исключив другую. Дифференцируя (3.48) по , а уравнение (3.49) по , получим уравнение для тока

(3.50)

Аналогично получатся уравнения для напряжения между проводниками

. (3.51)

Уравнения (3.50) и (3.51) являются одномерными волновыми уравнениями, где - постоянная с размерностью скорости.