6. Элементы теории специальных функций
6.1. Недостаточность элементарных функций для решений дифференциальных уравнений. Дифференциальные уравнения, как источник функций
Исторические сведения
Карл Фридрих Гаусс,
г.,
немецкий математик, астроном и физик.
В связи с вычислениями орбит планет
Гаусс занимался исследованиями
бесконечных рядов и, в частности,
гипергеометрическим рядом в
г.
Лежандр Андриен Мари, 1752 – 1833 г, - французский математик, член Парижской Академии Наук. Известен своими исследованиями по тригонометрии на поверхностях сфероидов, в теории гравитационного напряжения, фундаментальными результатами в теории чисел, теории вероятностей и математическом анализе. Открыл и исследовал в 1785 многочлены, получившие название полиномов Лежандра.
… … …
Решение дифференциальных уравнений резко выражается через интегралы от некоторых функций. В тех случаях, когда решение удается получить в виде конечных формул, содержащих операции интегрирования, говорят, что решение найдено в квадратурах. Но даже решение, найденное в квадратурах, часто приводит к рассмотрению не элементарных функций.
Например, интегралы
порождают функции
- интегральный синус,
- интегральная экспонента,
- интеграл вероятности,
которые являются решениями дифференциальных уравнений первого порядка.
Весьма важными в математике и ее приложениях функциями, заданными в интегральном виде, являются бэта- и гамма - функции Эйлера.
Бэта - функция определяется интегралом Эйлера первого рода
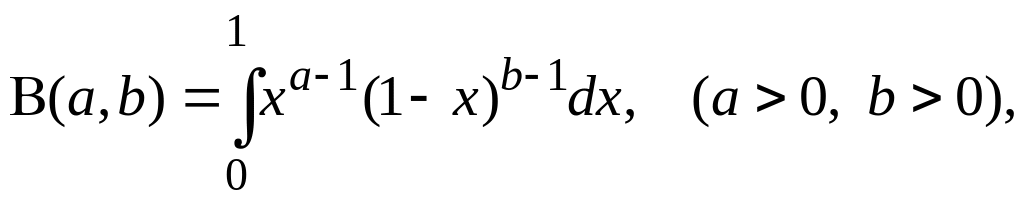
гамма-функция – интегралом Эйлера второго рода
Связь между бэта- и гамма – функциями определяется формулой
Для любого
справедливо
При натуральных
Основные элементарные функции, излучаемые в курсе элементарной алгебры, также можно рассматривать как решения дифференциальных уравнений. Например, функция
является решением уравнения
- решением уравнения
и
- решениями уравнения
- решением уравнения
Однако основные элементарные функции и функции, введенные выше через интегралы, не описывают многие процессы, протекающие в современных технических системах. Из теории специальных функций известно [1], что некоторые линейные дифференциальные уравнения второго порядка с переменными коэффициентами имеют решения, широко использующиеся в математической физике. Решения таких уравнений получили название “специальные функции”.
6.2. Гипергеометрическое уравнение и функции гипергеометрического типа
Многие функции в математической и теоретической физике, а также в теплотехнике и электро - радиотехнике возникают, как решения уравнений гипергеометрического типа.
Уравнениями гипергеометрического типа называются обыкновенные дифференциальные уравнения вида
(6.1)
где
и
- произвольные полиномы не выше второй
степени (вообще говоря, с комплексными
коэффициентами), а
- действительное или комплексное число.
Решения этого уравнения называются
функциями гипергеометрического типа.
Введенный термин – “гипергеометрический” не имеет никакого отношения к какой-либо гипергеометрии, например, к многомерным пространствам или к нееклидовой геометрии. Эта терминология возникла из-за того, что получаемые из уравнений типа (6.1) функции представляются в виде степенного ряда. В простейших случаях этот ряд превращается в геометрический, т.е. в геометрическую прогрессию.
В частном случае уравнение гипергеометрического типа (6.1) переходит в гипергеометрическое уравнение
(6.2)
называемое также уравнением Гаусса.
Решение уравнения (6.2) называется гипергеометрической функцией
(6.3)
Ряд (6.3) называют также гипергеометрическим
рядом или рядом Гаусса. Но этот ряд
обнаружил и узнал его замечательные
свойства еще Эйлер. При
ряд (6.3) обращается в геометрическую
прогрессию
При определенных значениях параметров
и
многие элементарные функции выражаются
через гипергеометрическую функцию.
Еще одной функцией, часто встречающиеся в решениях краевых задач математической физики является вырожденная гипергеометрическая функция
(6.4)
Ряд (6.4) называется вырожденным
гипергеометрическим рядом. В отличие
от гипергеометрического ряда (6.3) он
сходится при любых значениях
Функция
следующим образом выражается через
функцию Гаусса
Дифференциальное уравнение вырожденной
гипергеометрической функции
(6.5)
получается из уравнения (6.2) с помощью
замены
на
,
деления всех членов уравнения на
и предельным переходом
.
При
второе частное решение уравнения
(6.5), линейно - независимое с первым, дает
функция
Общее решение этого уравнения при
определяется формулой
где
и
- произвольные постоянные.
Через вырожденную гипергеометрическую
функцию выражаются многие специальные
функции. В частности, введенные в п.6.1
интегральный синус, интегральная
экспонента и интеграл вероятности
связаны с функцией
равенствами
где - постоянная Эйлера, равная
Через вырожденную гипергеометрическую функцию выражается также интегральный логарифм
другие специальные элементарные функции.
Вырожденную гипергеометрическую функцию в некоторых справочниках по специальным функциям называют функцией Куммера, а также эта функция обладает свойствами
где
- гамма - функция Эйлера.
Многочисленные свойства функции и других специальных функций приведены в справочнике [11].
Задачи для самостоятельного решения к п.6.1 и п.6.2.
Используя Гауссов ряд (6.3) и ряды для элементарных функций показать справедливость равенств:
1)
2)
3)
4)
5)
6)
7)
8)
9)
2. Используя ряд (6.4) и ряды для элементарных функций показать справедливость следующих равенств:
1)
2)
3)
4)
3. Получить из гипергеометрического
ряда в явном виде многочлен для функции
.