8.6. Метод Линдстедта – Пуанкаре

Как видно из формулы (8.34), уравнение Дюффинга описывает колебательный процесс. Первый член решения дает колебание линейной системы в принебрежении нелинейным слагаемым. Но в силу нелинейного характера уравнения процесс движения обогащается гармониками с частотами, кратными частоте колебаний линейной системы. В случае уравнения Дюффинга можно построить и его точное решение. Оказывается, что в точном решении уравнения частота колебаний зависит от амплитуды. Теоретически показано и это действительно наблюдается в реальных системах, что зависимость частоты от амплитуды колебаний характерна для многих нелинейных систем.

Существенной особенностью, не учитываемой при построении решения методом прямого асимптотического разложения, как раз и является такая зависимость. В этом кроется причина неравномерности прямого разложения – ведь в решении (8.34) угловая частота нелинейной системы равна частоте колебаний линейной системы и не зависит от характера нелинейности. Для получения равномерно пригодных асимптотических разложений разработан ряд методов, широко используемых для построения решения нелинейных задач, возникающих в различных разделах механики, физики и инженерных наук. Одним из эффективных асимптотических методов построения равномерно пригодных периодических решений нелинейных дифференциальных уравнений является метод Линдстедта – Пуанкаре. В его основу положены две существенные идеи:

1. Деформирование частоты колебаний с тем, чтобы она зависела от малого параметра – меры нелинейности системы;

2. Исключение секулярных членов в разложении решения по малому параметру на основе выбора поправочных членов к частоте колебаний линейной системы.

Проиллюстрируем метод на примере уравнения Дюффинга (8.16). Введем неизвестную частоту непосредственно в дифференциальное уравнение (8.16) с помощью преобразования

, (8.35)

где - введенное ранее в уравнение (8.15) безразмерное время, - новая безразмерная частота, определяемая через и параметр .

Используя правило дифференцирования сложной функции, получаем

В результате уравнение (8.16) перепишется в виде

, (8.36)

где штрихами обозначена производная по новой переменной . Неизвестными величинами в уравнении (8.36) являются и . Будем искать их в виде разложений по степеням малого параметра , т.е. положим

(8.37)

. (8.38)

Главный член разложения для представляет собой частоту линейной системы . Исходя из требования равномерной пригодности разложения для функции при всех , в процессе вычислений можно определить все последующие поправки к частоте линейной системы.

Подставка (8.37) и (8.38) в уравнение (8.36) дает

откуда после выполнения необходимых действий имеем

.

Приравнивая нулю коэффициенты при и , получаем

, (8.39)

. (8.40)

Общее решение уравнения (8.39) дается формулой

,

где и - произвольные постоянные. С учетом этого уравнение (8.40) переписывается в виде

,

или, используя формулу понижения степени тригонометрической функции,

. (8.41)

Уравнение (8.41) является линейным дифференциальным уравнением второго порядка, в правой части которого имеются две функции специального вида. Частное решение неоднородного уравнения (8.41) разыскиваем в виде суммы двух частных решений

Применяя метод неопределенных коэффициентов, находим . В результате получим частное решение уравнения (8.41)

. (8.42)

Первый член в частном решении (8.42) и является причиной неравномерности разложения, на что было указано в предыдущем пункте. Чтобы избежать появление секулярного члена в решении, подберем параметр так, чтобы коэффициент обратился в нуль.

Отметим, что для получения выражения для ₁ не было необходимости находить частное решение . Достаточно было в самом уравнении (8.41) приравнять нулю коэффициент при cos( ).

Таким образом, используя (8.42), получаем приближенное решение уравнение Дюффинга

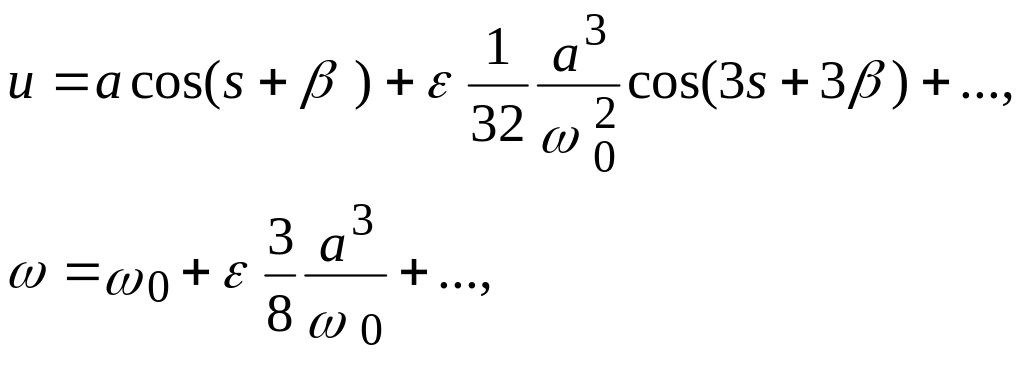
Подставив из равенства (8.35) получим решение через старую безразмерную переменную

(8.43)

Разложение решения (8.43) по малому параметру будет равномерно пригодным разложением первого порядка, поскольку в нем отсутствуют секулярные члены, а поправка (член пропорциональный ) оказывается малой по сравнению с главным членом разложения.

Задачи для самостоятельного решения к.п. 8.5 –8. 6.

1. Рассмотреть уравнение Ван – дер – поля

.

Построить двучленное прямое разложение. Выяснить, является ли это разложение равномерно пригодным. Построить равномерное разложение методом Линдстедта – Пуанкаре.

2. Используя метод Линдстедта – Пуанкаре построить равномерно пригодное разложение первого порядка для уравнения

.

СПИСОК ЛИТЕРАТУРЫ

1. Пискунов Н.С. - Дифференциальное и интегральное исчисления. – М.: Наука, 1985, т. 2. 576 с.

2. Бугров Я.Г., Никольский В.В. Дифференциальные уравнения. Кратные интегралы. Ряды. М.: Наука, 1981.- 448 с.

3. Ефимов А. В. Математический анализ. Специальные разделы. Т.1. Общие функциональные ряды и их приложение. – М.: Высшая школа, 1980. – 279 с.

4. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. Ч. 2. – М.: Высшая Школа, 1986. – 415 с.

5. Берман Г.Н. - Сборник задач по курсу математического анализа. – М.: Наука, 1989, 416 с.

6. Никольский В.В. Электродинамика и распространение радиоволн. М.: Наука, 1978. - 545 с.

7. Двайт Г.Б. Таблицы интегралов и другие математические формулы. М.: Наука, 1978. – 228 с.

8. Бронштейн Н.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. М.: Наука, 1986. - 544 с.

9. Будак Б.М., Фомин С.В. Кратные интегралы и ряды. - М.: Наука, 1967. – 607 с.

10. Фейнман Р., Лейтон Р., Сэнде М. Фейнмановские лекции по физике. Т.5. М.: Мир, 1966. - 296 с.

11. Е. Янке, Ф. Эмде, Ф. Леш - Специальные функции. – М.: Наука, 1977, 342 с.

12. Методические указания №39-2004 «Специальные функции и решение дифференциальных уравнений в рядах» Бырдин А.П., Глушак А.В. и др.

13. А.Ф. Никифоров, В.Б. Уваров - Основы теории специальных функций. – М.: Наука, 1974, 303 с.

С О Д Е Р Ж А Н И Е

Введение………………………………………………………....... 3