1.3. Тригонометрические ряды Фурье
В приложениях математики к задачам радиотехники, теплоэнергетики и физики наиболее распространенной полной ортонормированной системой функций является тригонометрическая система, ортогональная при - l x l
(1.8)
Вычислив интегралы, можно убедится в справедливости равенств:
Из формул (1.7) для тригонометрической системы функций (1.8) получаем коэффициенты Фурье функций f(x)
(1.9)
(n = 1,2,…).
Ряд вида
(1.10)
называется тригонометрическим рядом Фурье порожденным функцией , в честь французского математика Фурье Жан Батиста Жозефа (1768 – 1830 г.), главные открытия которого связаны с построением математической теории теплопроводности твердых тел.
В частности, если функция четная, то её ряд Фурье имеет вид:
(1.11)
Ряд Фурье нечетной функции имеет вид
(1.12)
Возникает важный вопрос: при каких условиях на функцию ее ряд Фурье представляет эту функцию и в соотношениях (1.10) - (1) можно поставить знак равенства? Для определенного класса функций ответ на этот вопрос дается теоремой.
Теорема. ( О разложении.) Пусть
кусочно-гладкая на отрезке
функция f(x)
периодически с периодом 2l
продолжена на всю бесконечную прямую.
Тогда тригонометрический ряд Фурье
функции (1.10) сходится в каждой точке x
из (- ,)
к значению f(x)
в каждой точке непрерывности и к
значению
в точке разрыва, т.е. имеет место равенство
(1.13)
где
,
,
вычисляются по формулам (1.9), f(x±0)
– предельные значения функции слева и
справа в точке разрыва.
Кусочная гладкость функции на отрезке
означает, что отрезок можно разбить
на конечное число промежутков, внутри
каждого из которых
непрерывна и имеет непрерывную
производную, причем
и
имеют конечные пределы на концах любого
промежутка.
В комплексной форме тригонометрический ряд Фурье (1.10) принимает вид
(1.14)
где
– комплексные коэффициенты Фурье,
связанные с
и
формулами
=
,
=
,
,
,
причем для вещественной функции
справедливо
.
Если функция
задана в промежутке
,
то для разложения ее в ряд Фурье можно
рассмотреть периодическое продолжение
разными способами.
1. Можно считать, что
,
т.е. продолжение функции имеет период
равный
.
Ее ряд Фурье будет содержать и косинусы,
и синусы.
2. Можно считать, что
,
где
,
,
т.е.
продолженная функция имеет период
и нечетная.
3. Можно считать, что
,
где
, ,
т.е. продолженная функция имеет период и четная.
Задачи для самостоятельного решения
1. 4, гл.3, §8 №485, №486, №489, №490, №493, №497, №498.
2. 5, гл.15, §2 №4373, №4375, №4386, №4391, №4392.
Литература к п. 1.3. 1, гл.17, §1-7, §10, §12, §15-16, 2, гл.4, §4.1 - 4.6, §4.9-4.11, 3, гл.8, §1-3.
1.4. Интегральная формула Фурье. Интеграл Фурье
Если отрезок
,
на котором функция
разлагается в тригонометрический ряд
Фурье, неограниченно возрастает (
),
то ряд Фурье превращается в интеграл
Фурье. Происходит качественный
скачок: заданная на конечном отрезке
функция разлагается в ряд гармонических
колебаний (1.13), частоты которых образуют
дискретную последовательность; функция
же заданная на всей оси или полуоси,
разлагается в интеграл, являющийся
суммой гармонических колебаний с
частотами, непрерывно заполняющими всю
полуось
Пусть функция разлагается в ряд Фурье, т.е. имеет место равенства (1.13), где в точках непрерывности в левой части равенства стоит . Подставив в (1.13) выражение для коэффициентов Фурье из (1.9), получим после преобразований
=
,
(1.15)
где переменную интегрирования обозначили t.
Если является абсолютно интегрируемой на всей оси, т.е.
,
то при
первое слагаемое в (1.15) стремиться к
нулю. Следовательно,
=
,
(1.16)
Обозначим
,
.
Тогда (1.16) можно записать так
=
,
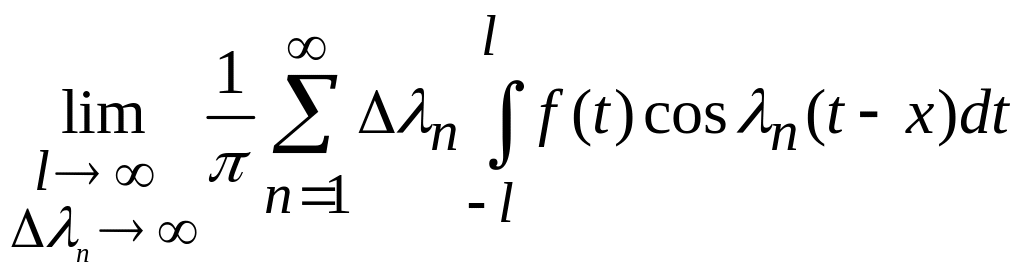(1.17)
При интеграл в (1.17) становится несобственным интегралом от - до ; сумма в (1.17) является интегральной суммой. Поэтому из (1.17) получаем
=
,
(1.18)
где в левой части вместо
будет стоять
,
если x является
точкой разрыва функции.
Равенство (1.18) называется интегральной формулой Фурье, а интеграл в правой части – интегралом Фурье.