
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко л.П. Цуканова
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко л.П. Цуканова
- •Введение
- •1. Ортогональные системы функций и обобщенные ряды Фурье. Интегралы Фурье
- •1.1. Исторические замечания
- •1.2. Гильбертово пространство. Ряды Фурье в гильбертовом пространстве
- •1.3. Тригонометрические ряды Фурье
- •1.4. Интегральная формула Фурье. Интеграл Фурье
- •1.5. Условия представимости функции интегралом Фурье
- •1.6. Комплексная форма интеграла Фурье. Преобразование Фурье
- •Преобразование Лапласа и его приложения
- •1.1. Свойства преобразования Лапласа
- •2.2. Решение дифференциальных уравнений операционным методом
- •Импульсные функции и их приложение к решению дифференциальных уравнений
- •Приложение операционного метода к решению систем линейных дифференциальных уравнений с постоянными коэффициентами
- •2.5. Индивидуальные задания
- •Ответы к индивидуальным заданиям
- •Задачи механики и физики, приводящие к основным уравнениям математической физики
- •3.1. Понятие уравнения в частных производных и его решения. Основные уравнения математической физики. Уравнения современной математической физики
- •3.2. Уравнения Пуассона и Лапласа. Вывод уравнений для потенциала электрического поля
- •3.3. Получение уравнения Гельмгольца из уравнений электромагнитного поля
- •3.4. Уравнение распространения тепла в изотропном твердом теле
- •3.5. Уравнение колебаний струны
- •4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи Коши
- •4.1. Распространение тепла в неограниченном стержне. Фундаментальное решение уравнения теплопроводности
- •4.2. Метод Фурье для одномерного уравнения теплопроводности. Распространение тепла в ограниченном стержне
- •4.3. Общее решение волнового уравнения в случае одной пространственной переменной. Решение Даламбера
- •4.4. Задача Коши для одномерного волнового уравнения. Формула Даламбера
- •4.5. Колебания ограниченной струны. Решение методом Фурье
- •5. Метод Фурье для уравнений математической физики в двумерном и трехмерном пространствах
- •5.1. Оператор Лапласа в декартовых и криволинейных координатах. Граничные задачи для уравнений Лапласа и Пуассона
- •5.2. Разделение переменных в уравнении Лапласа в декартовой и сферической системах координат
- •5.3. Определение потенциала электрического поля внутри параллелепипеда
- •5.4. Разделение переменных в уравнении Лапласа в цилиндрических координатах
- •5.5. Задача Дирихле для уравнения Лапласа в круге. Интеграл Пуассона
- •5.6. Распространение тепла в бесконечном цилиндре
- •5.7. Распространение электромагнитных волн в цилиндрическом волноводе
- •Решение уравнения Гельмгольца методом Фурье
- •5.8. Движение электрона в атоме водорода. Квантовый подход
- •6. Элементы теории специальных функций
- •6.1. Недостаточность элементарных функций для решений дифференциальных уравнений. Дифференциальные уравнения, как источник функций
- •6.2. Гипергеометрическое уравнение и функции гипергеометрического типа
- •6.3. Частные случаи гипергеометрической функции: цилиндрические функции Бесселя
- •6.4. Частные случаи гипергеометрической функции: ортогональные полиномы Лежандра
- •7. Функциональные и степенные ряды и их приложения к решению дифференциальных уравнений
- •7.1 Функциональные ряды. Сходимость и равномерная сходимость
- •7.2. Свойства равномерно сходящихся рядов. Признак равномерной сходимости
- •7.3. Степенные ряды. Интервал сходимости, радиус сходимости
- •7.4. Свойства степенных рядов
- •7.5. Арифметические операции и другие действия над степенными рядами
- •7.6. Разложение функций в степенные ряды
- •7.7. Обобщения степенных рядов – интегро – степенные ряды и ряды Вольтерра
- •8. Приближенно-аналитические методы решения дифференциальных уравнений
- •8.1. Необходимость асимптотических методов
- •8.2. Калибровочные функции. Символы порядка
- •8.3. Пример асимптотического разложения. Определение асимптотического ряда
- •8.4. Асимптотические последовательности и асимптотические разложения
- •8.5. Простейшие асимптотические методы решения дифференциальных уравнений
- •8.6. Метод Линдстедта – Пуанкаре
- •1. Ортогональные системы функций .И обобщенные ряды Фурье. Интегралы Фурье……………………………………..... 4
- •2. Преобразование Лапласа и его приложения…………….19
- •2.3. Импульсные функции и их приложение к решению дифференциальных уравнений …………….……….……..…... 38
- •3. Задачи механики и физики, приводящие к основным уравнениям математической физики ……………………......76
- •4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи ……...……………107
- •5. Метод Фурье для уравнений математической физики в двумерном и трехмерном пространствах .......…………….133
- •6. Элементы теории специальных функций.........................179
- •8. Приближенно-аналитические методы решения дифференциальных уравнений ….........................................221
- •9. Список литературы………………………………………..247
- •394026 Воронеж, Московский просп., 14
4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи Коши
4.1. Распространение тепла в неограниченном стержне. Фундаментальное решение уравнения теплопроводности
Для решения краевых задач математической физики широко применяется преобразование Фурье. Причина этого заключается в том, что образ Фурье искомой функции часто удовлетворяет более простому уравнению, чем сама искомая функция. При решении краевых задач математической физики преобразование Фурье используется по следующей схеме:
1. Подвергают преобразованию Фурье обе части уравнения, которому удовлетворяет искомая функция; отсюда получают уравнение для ее Фурье-образа;
2. Из этого уравнения находят образ Фурье искомого решения первоначального уравнения;
3. Используя обратное преобразование Фурье находят искомую функцию.
Рассмотрим распределение температуры
в неограниченном в обе стороны
прямолинейном стержне в произвольный
момент времени
![]() ,
если ее распределение в начальный момент
времени
известно. Стержень считаем теплопроводным
от окружающей среды по боковой поверхности
и его сечение считаем настолько малым,
что всем точкам сечения в каждый момент
времени можно приписать одну и ту же
температуру.
,
если ее распределение в начальный момент
времени
известно. Стержень считаем теплопроводным
от окружающей среды по боковой поверхности
и его сечение считаем настолько малым,
что всем точкам сечения в каждый момент
времени можно приписать одну и ту же
температуру.
Задача заключается в нахождении решения уравнения теплопроводности в бесконечной области по известному начальному условию:
,
![]() ,
,
(4.1)
,
,
(4.1)
![]() ,
,
(4.2)
,
,
(4.2)
где
– заданная функция, абсолютно интегрируемая
на оси
![]() .
.
Решаем эту задачу, применяя преобразование
Фурье по переменной x.
Обозначим через
![]() образ Фурье функции
образ Фурье функции
![]()
 .
(4.3)
.
(4.3)
Умножим обе части уравнения (4.1) на
![]() и проинтегрируем по
от
и проинтегрируем по
от
![]() до
до
![]() ,
предполагая, что функция
и ее производные достаточно быстро
стремятся к нулю при
,
предполагая, что функция
и ее производные достаточно быстро
стремятся к нулю при
![]() .
Интегрируя левую часть, получим
.
Интегрируя левую часть, получим
 .(4.4)
.(4.4)
Для преобразования правой части уравнения используем интегрирование по частям:
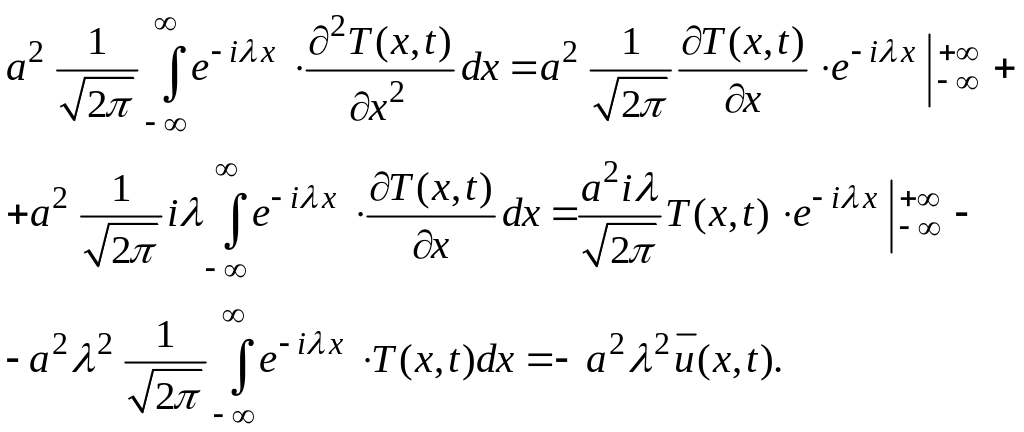 (4.5)
(4.5)
При получении (4.5) учли, что неинтегральные
члены обращаются в нуль, в силу
ограниченности функции
![]() и предполагаемого поведения функции
:
и предполагаемого поведения функции
:
![]() .
.
Приравнивая (4.4) и (4.5) получим обыкновенное дифференциальное уравнение для образа Фурье искомой функции
![]() .
(4.6)
.
(4.6)
Начальное условие для функции получим из начального условия (4.2), выполнив преобразование Фурье
 ,
,
(4.7)
![]() .
.
Разделяя переменные в уравнении (4.6), получаем
![]() ,
,
![]() .
.
Отсюда
![]() .
(4.8)
.
(4.8)
Определим постоянную С с помощью начального условия (4.7)
![]() .
.
Подставив это значение С в равенство (4.8), получим для Фурье-образа искомой функции следующее выражение
![]() .
(4.9)
.
(4.9)
Теперь осталось перейти к третьему
этапу решения задачи найти саму функцию
по найденному ее образу Фурье (4.9). Для
этого применим к равенству (4.9) обратное
преобразование Фурье, подставив вместо
![]() его явное выражение из (4.7). Умножив (4.9)
на
его явное выражение из (4.7). Умножив (4.9)
на
![]() и интегрируем по, получаем
и интегрируем по, получаем
 .(4.10)
.(4.10)
Подставим в правую часть выражение для экспоненты с мнимым аргументом по формуле Эйлера
![]() .
.
Учитывая, что
 ,
,
если
![]() - четная функция, а также равенство
- четная функция, а также равенство
 ,
,
если - нечетная функция, имеем
 ,
,
 .
.
Последний интеграл является известной и часто встречающейся в теории теплопроводности и теории диффузии функцией. Воспользуемся [7] формулой 861.20, получим
 .
.
Подставив эти результаты в выражении (4.10), получим решение уравнения (4.1) при начальном условии (4.2)
 . (4.11)
. (4.11)
Полученную формулу называют формулой Пуассона. Функция аргументов и
 (4.12)
(4.12)
называется фундаментальным решением уравнения теплопроводности (4.1). Она удовлетворяет уравнению теплопроводности. Решение уравнения теплопроводности с начальным условием в виде (4.11) является сверткой фундаментального решения с начальной функцией.
Рассмотрим физический смысл фундаментального
решения уравнения теплопроводности.
Выделим малый элемент стержня
![]() вблизи точки
вблизи точки
![]() и зададим начальное распределение
температуры в виде
и зададим начальное распределение
температуры в виде
![]()
![]()
Физически это означает, что в начальный
момент времени
этому элементу стержня передали
количества тепла
![]() (
-
линейная плотность материала,
(
-
линейная плотность материала,
![]() -удельная
теплоемкость), которое привело к повышению
температуры на этом элементе на величину
-удельная
теплоемкость), которое привело к повышению
температуры на этом элементе на величину
![]() .
В последующие моменты времени
распределение температуры в стержне
определяется формулой (4.11), которая в
данном случае принимает вид
.
В последующие моменты времени
распределение температуры в стержне
определяется формулой (4.11), которая в
данном случае принимает вид

Если распределять то же самое количество
тепла Q на все меньшем
участке
![]() ,
то в пределе в точке
стержню сообщается количества тепла
Q. Это означает, что в
точке
стержня в момент
действует мгновенный точечный источник
тепла напряжения Q.
От действия такого мгновенного точечного
источника тепла в стержне получается
распределение температур
,
то в пределе в точке
стержню сообщается количества тепла
Q. Это означает, что в
точке
стержня в момент
действует мгновенный точечный источник
тепла напряжения Q.
От действия такого мгновенного точечного
источника тепла в стержне получается
распределение температур
 ,
,
(4.13)
где применим теорему о среднем для определенного интеграла
 ,
,
![]() .
.
Предел последнего выражения при
![]() ,
а значит
,
а значит
![]() ,
и приводим к выражению (4.13).
,
и приводим к выражению (4.13).
Таким образом, фундаментальное решение
(4.12) дает распределение температуры,
которое вызывается мгновенным точечным
источником тепла напряжения
![]() ,
помещенным в начальный момент времени
в точке
,
помещенным в начальный момент времени
в точке
![]() стержня.
стержня.
В соответствии с этим можно дать
физическое толкование и решению (4.11).
Для того, чтобы придать сечению
стержня температуру
![]() в начальный момент времени, мы должны
на малом элементе
в начальный момент времени, мы должны
на малом элементе
![]() около этой точки распределить количество
тепла
около этой точки распределить количество
тепла
![]() ,
т. е. поместить в точке
,
т. е. поместить в точке
![]() мгновенный точечный источник тепла
напряжения
мгновенный точечный источник тепла
напряжения
![]() .
Распределение температуры, вызываемое
этим мгновенным точечным источником
будет равно
.
Распределение температуры, вызываемое
этим мгновенным точечным источником
будет равно
 .
.
Общее действие от начальной температуры
![]() во всех точках стержня складывается от
этих элементов, что и приводит к формуле
(4.11).
во всех точках стержня складывается от
этих элементов, что и приводит к формуле
(4.11).
